11. Credit Valuation Adjustment (CVA) Framework
Credit Valuation Adjustment (CVA) Overview
11.1. The risk-weighted assets for Credit Value Adjustment risk are determined by multiplying the capital requirements calculated as set out in Chapter 11 of this Framework by 12.5.
11.2. In the context of this framework, CVA stands for Credit Valuation Adjustment specified at a counterparty level. CVA reflects the adjustment of default risk-free prices of derivatives and Securities Financing Transactions (SFTs) due to a potential default of the counterparty.
11.3. Unless explicitly specified otherwise, the term CVA in this framework means regulatory CVA. Regulatory CVA may differ from CVA used for accounting purposes as follows:
(1) regulatory CVA excludes the effect of the bank's own default; and
(2) several constraints reflecting best practice in accounting CVA are imposed on calculations of regulatory CVA.
11.4. CVA risk is defined as the risk of losses arising from changing CVA values in response to changes in counterparty credit spreads and market risk factors that drive prices of derivative transactions and SFTs.
11.5. The capital requirement for CVA risk must be calculated by all banks involved in covered transactions in both banking book and trading book. Covered transactions include:
(1) all derivatives except those transacted directly with a qualified central counterparty and except those transactions meeting the conditions of 8.14 to 8.16 of this framework; and.
(2) SFTs that are fair-valued by a bank for accounting purposes, if SAMA determines that the bank's CVA loss exposures arising from SFT transactions are material. In case the bank deems the exposures immaterial, the bank must justify its assessment to SAMA by providing relevant supporting documentation.
(3) SFTs that are fair-valued for accounting purposes and for which a bank records zero for CVA reserves for accounting purposes are included in the scope of covered transactions.
11.6. The CVA risk capital requirement is calculated for a bank's “CVA portfolio” on a standalone basis. The CVA portfolio includes CVA for a bank's entire portfolio of covered transactions and eligible CVA hedges.
11.7. Two approaches are available for calculating CVA capital: the standardized approach (SA-CVA) and the basic approach (BA-CVA). Banks must use the BA- CVA unless they receive approval from Saudi Central Bank (SAMA) to use the SA-CVA.40
11.8. Banks that have received approval of Saudi Central Bank (SAMA) to use the SA- CVA may carve out from the SA-CVA calculations any number of netting sets. CVA capital for all carved out netting sets must be calculated using the BA-CVA. When applying the carve-out, a legal netting set may also be split into two synthetic netting sets, one containing the carved-out transactions subject to the BA-CVA and the other subject to the SA-CVA, subject to one or both of the following conditions:
(1) the split is consistent with the treatment of the legal netting set used by the bank for calculating accounting CVA (e.g. where certain transactions are not processed by the front office/accounting exposure model); or
(2) SAMA approval to use the SA-CVA is limited and does not cover all transactions within a legal netting set.
11.9. For banks that are below the materiality threshold where aggregate notional amount of non-centrally cleared derivatives is less than or equal to 446 billion SAR may opt not to calculate its CVA capital requirements using the SA-CVA or BA-CVA and instead choose an alternative treatment.
(1) Subject to the above conditions and treatment,
a. Banks may choose to set its CVA capital equal to 100% of the bank's capital requirement for counterparty credit risk (CCR);
b. Banks CVA hedges will not be recognized; and
c. Banks must apply this treatment to the bank's entire portfolio instead of the BA-CVA or the SA-CVA.
(2) SAMA, however, may not allow banks to apply the above treatment if it determines that CVA risk resulting from the bank's derivative positions materially contributes to the bank's overall risk.
11.10. Eligibility criteria for CVA hedges are specified in11.17 to 11.19 for the BA-CVA and in 11.37 to 11.39 for the SA-CVA.
11.11. CVA hedging instruments can be external (i.e. with an external counterparty) or internal (i.e. with one of the bank's trading desks).
(1) All external CVA hedges (including both eligible and ineligible external CVA hedges) that are covered transactions must be included in the CVA calculation for the counterparty to the hedge.
(2) All eligible external CVA hedges must be excluded from a bank's market risk capital requirement calculations under Chapter 2 through Chapter 14 of the Minimum Capital Requirements for Market Risk.
(3) Ineligible external CVA hedges are treated as trading book instruments and are capitalized under Chapter 2 through Chapter 14 of the Minimum Capital Requirements for Market Risk.
(4) An internal CVA hedge involves two perfectly offsetting positions: one of the CVA desk and the opposite position of the trading desk.
a) If an internal CVA hedge is ineligible, both positions belong to the trading book where they cancel each other, so there is no impact on either CVA portfolio or the trading book.
b) If an internal CVA hedge is eligible, the CVA desk's position is part of the CVA portfolio where it is capitalized as set out in this chapter, while the trading desk's position is part of the trading book where it is capitalized as set out in Chapter 2 through Chapter 14 of the Minimum Capital Requirements for Market Risk.
(5) If an internal CVA hedge involves an instrument that is subject to curvature risk, default risk charge or the residual risk add-on under the standardized approach as set out in Chapter 6 to Chapter 9 of the Minimum Capital Requirements for Market Risk, it can be eligible only if the trading desk that is the CVA desk's internal counterparty executes a transaction with an external counterparty that exactly offsets the trading desk's position with the CVA desk.
11.12. Banks that use the BA-CVA or the SA-CVA for calculating CVA capital requirements may cap the maturity adjustment factor at 1 for all netting sets contributing to CVA capital when they calculate CCR capital requirements under the Internal Ratings Based (IRB) approach.
40 Note that this is in contrast to the application of the market risk approaches set out in Chapter 3 of the Minimum Capital Requirements for Market Risk, where banks do not need SAMA approval to use the standardized approach.
Basic Approach for Credit Valuation Adjustment Risk
11.13. The BA-CVA calculations may be performed either via the reduced version or the full version. A bank under the BA-CVA approach can choose whether to implement the full version or the reduced version at its discretion. However, all banks using the BA-CVA must calculate the reduced version of BA-CVA capital requirements as the reduced BA-CVA is also part of the full BA-CVA capital calculations as a conservative means to limit hedging recognition.
(1) The full version recognizes counterparty spread hedges and is intended for banks that hedge CVA risk.
(2) The reduced version eliminates the element of hedging recognition from the full version. The reduced version is designed to simplify BA-CVA implementation for less sophisticated banks that do not hedge CVA.
Reduced version of the BA-CVA (hedges are not recognized)
11.14. The capital requirement for CVA risk under the reduced version of the BA-CVA (DSBA-CVA × Kreduced, where the discount scalar DSBA-CVA = 0.65) is calculated as follows (where the summations are taken over all counterparties that are within scope of the CVA charge), where:
(1) SCVAC is the CVA capital requirement that counterparty c would receive if considered on a stand-alone basis (referred to as “stand-alone CVA capital” below). See 11.15 for its calculation;
(2) ρ= 50%. It is supervisory correlation parameter. Its square, ρ2 = 25% represents the correlation between credit spreads of any two counterparties.41 In the formula below, the effect of p is to recognize the fact that the CVA risk to which a bank is exposed is less than the sum of the CVA risk for each counterparty, given that the credit spreads of counterparties are typically not perfectly correlated; and
(3) The first term under the square root in the formula below aggregates the systematic components of CVA risk, and the second term under the square root aggregates the idiosyncratic components of CVA risk.
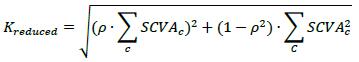
11.15. The stand-alone CVA capital requirements for counterparty c that are used in the formula in 11.14 (SCVAc) is calculated as follows (where the summation is across all netting sets with the counterparty), where:
(1) RWc is the risk weight for counterparty c that reflects the volatility of its credit spread. These risk weights are based on a combination of sector and credit quality of the counterparty as prescribed in 11.16.
(2) MNS is the effective maturity for the netting set NS. For banks that have SAMA’s approval to use IMM, NNS is calculated as per 7.20 and 7.21 of this framework, with the exception that the five year cap in 7.20 is not applied. For banks that do not have SAMA’s approval to use IMM, MNS is calculated according to chapter 12.46 to 12.54 of the Minimum Capital Requirements for Credit Risk, with the exception that the five-year cap in chapter 12.46 of the Minimum Capital Requirements for Credit Risk is not applied.
(3) EADNS is the exposure at default (EAD) of the netting set NS, calculated in the same way as the bank calculates it for minimum capital requirements for CCR.
(4) DFNS is a supervisory discount factor. It is 1 for banks using the IMM to calculate EAD, and is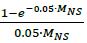 
for banks not using IMM.42
(5) ∝ = 1.4.43
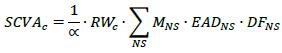
11.16. The supervisory risk weights (RWc) are given in Table 1. Credit quality is specified as either investment grade (IG), high yield (HY), or not rated (NR). Where there are no external ratings or where external ratings are not recognized within a jurisdiction, banks may, subject to SAMA's approval, map the internal rating to an external rating and assign a risk weight corresponding to either IG or HY. Otherwise, the risk weights corresponding to NR is to be applied.
Table 1: Supervisory risk weights, RWc Sector of counterparty Credit quality of counterparty IG HY and NR Sovereigns including central banks, multilateral development banks 0.5% 2.0% Local government, government-backed nonfinancials, education and public administration 1.0% 4.0% Financials including government-backed financials 5.0% 12.0% Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying 3.0% 7.0% Consumer goods and services, transportation and storage, administrative and support service activities 3.0% 8.5% Technology, telecommunications 2.0% 5.5% Health care, utilities, professional and technical activities 1.5% 5.0% Other sector 5.0% 12.0% Full version of the BA-CVA (hedges are recognized)
11.17. As set out in 11.13(1) the full version of the BA-CVA recognizes the effect of counterparty credit spread hedges. Only transactions used for the purpose of mitigating the counterparty credit spread component of CVA risk, and managed as such, can be eligible hedges.
11.18. Only single-name credit default swaps (CDS), single-name contingent CDS and index CDS can be eligible CVA hedges.
11.19. Eligible single-name credit instruments must:
(1) reference the counterparty directly; or
(2) reference an entity legally related to the counterparty; where legally related refers to cases where the reference name and the counterparty are either a parent and its subsidiary or two subsidiaries of a common parent; or
(3) reference an entity that belongs to the same sector and region as the counterparty.
11.20. Banks that intend to use the full version of BA-CVA must calculate the reduced version (Kreduced) as well. Under the full version, capital requirement for CVA risk DSBA-CVA × Kfull is calculated as follows, where DSBA-CVA = 0.65, and β= 0.25 is the SAMA supervisory parameter that is used to provide a floor that limits the extent to which hedging can reduce the capital requirements for CVA risk:
Kfull = β ∙ Kreduced + (1 - β) ∙ Khedged
11.21. The part of capital requirements that recognizes eligible hedges (Khedged) is calculated formulas follows (where the summations are taken over all counterparties c that are within scope of the CVA charge), where:
(1) Both the stand-alone CVA capital (SCVAc) and the correlation parameter (ρ) are defined in exactly the same way as for the reduced form calculation BA-CVA.
(2) SNHc is a quantity that gives recognition to the reduction in CVA risk of the counterparty c arising from the bank's use of single-name hedges of credit spread risk. See 11.23 for its calculation.
(3) IH is a quantity that gives recognition to the reduction in CVA risk across all counterparties arising from the bank's use of index hedges. See 11.24 for its calculation.
(4) HMAc is a quantity characterizing hedging misalignment, which is designed to limit the extent to which indirect hedges can reduce capital requirements given that they will not fully offset movements in a counterparty's credit spread. That is, with indirect hedges present Khedged cannot reach zero. See 11.25 for its calculation.
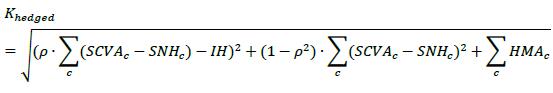
11.22. The formula for Khedged in 11.21 comprises three main terms as below:
(1) The first term (ρ • ∑c(SCVAc - SNHc) - IH)2 aggregates the systematic components of CVA risk arising from the bank's counterparties, the single name hedges and the index hedges.
(2) The second term (1- ρ2) • ∑c(SCVAc - SNHc)2 aggregates the idiosyncratic components of CVA risk arising from the bank's counterparties and the single-name hedges.
(3) The third term ∑cHMAc aggregates the components of indirect hedges that are not aligned with counterparties' credit spreads.
11.23. The quantity SNHc is calculated as follows (where the summation is across all single name hedges h that the bank has taken out to hedge the CVA risk of counterparty c), where:
(1) rhc is the supervisory prescribed correlation between the credit spread of counterparty c and the credit spread of a single-name hedge h of counterparty c. The value of rhc is set out the table 2 of 11.26. It is set at 100% if the hedge directly reference the counterparty c, and set at lower values if it does not.
(2) MhSN is the remaining maturity of single-name hedge h.
(3) BhSN is the notional of single-name hedge h. For single-name contingent credit default swaps (CDS), the notional is determined by the current market value of the reference portfolio or instrument.
(4) DFhSN is the supervisory discount factor calculated as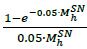 
.
(5) RWh is the supervisory risk weight of single-name hedge h that reflects the volatility of the credit spread of the reference name of the hedging instrument. These risk weights are based on a combination of sector and credit quality of the reference name of the hedging instrument as prescribed in Table 1 of 11.16.
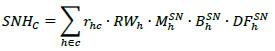
11.24. The quantity IH is calculated as follows (where the summation is across all index hedges i that the bank has taken out to hedge CVA risk), where:
(1) Miind is the remaining maturity of index hedge i.
(2) Biind is the notional of the index hedge i.
(3) DFiind is the supervisory discount factor calculated as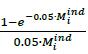 
(4) RWi is the supervisory risk weight of the index hedge i. RWi is taken from the Table 1 of 11.16 based on the sector and credit quality of the index constituents and adjusted as follows:
(a) For an index where all index constituents belong to the same sector and are of the same credit quality, the relevant value in the Table 1 of 11.16 is multiplied by 0.7 to account for diversification of idiosyncratic risk within the index.
(b) For an index spanning multiple sectors or with a mixture of investment grade constituents and other constituents, the name-weighted average of the risk weights from the Table 1 of 11.16 should be calculated and then multiplied by 0.7.
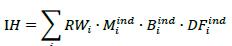
11.25. The quantity HMAc is calculated as follows(where the summation is across all single name hedges h that have been taken out to hedge the CVA risk of counterparty c), where rhc, MhSN, BhSN, DFhSN and RWh have the same definitions as set out in 11.23.
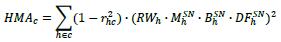
11.26. The supervisory prescribed correlations rhc between the credit spread of counterparty c and the credit spread of its single-name hedge h are set in Table 2 as follows:
Table 2: Correlations between credit spread of counterparty and single-name hedge Single-name hedge h of counterparty c Value of rhc references counterparty c directly 100% has legal relation with counterparty c 80% shares sector and region with counterparty c 50% 41 One of the basic assumptions underlying the BA-CVA is that systematic credit spread risk is driven by a single factor. Under this assumption, ρ can be interpreted as the correlation between the credit spread of a counterparty and the single credit spread systematic factor.
42 DF is SAMA discount factor averaged over time between today and the netting set's effective maturity date. The interest rate used for discounting is set at 5%, hence 0.05 in the formula. The product of EAD and effective maturity in the BA-CVA formula is a proxy for the area under the discounted expected exposure profile of the netting set. The IMM definition of effective maturity already includes this discount factor, hence DF is set to 1 for IMM banks. Outside IMM, netting set effective maturity is defined as an average of actual trade maturities. This definition lacks discounting, so SAMA discount factor is added to compensate for this.
43 ∝ is the multiplier used to convert Effective Expected Positive Exposure (EEPE) to EAD in both SACCR and IMM. Its role in the calculation, therefore, is to convert the EAD of the netting set (EADNS) back to EEPE.Standardized Approach for Credit Valuation Adjustment Risk
11.27. The SA-CVA is an adaptation of the standardized approach for market risk set out in Chapter 6 to Chapter 9 of the Minimum Capital Requirements for Market Risk. The primary differences of the SA-CVA from the standardized approach for market risk are:
(1) The SA-CVA features a reduced granularity of market risk factors; and
(2) The SA-CVA does not include default risk and curvature risk.
11.28. Under the SA-CVA, capital requirements must be calculated and reported to SAMA at the same frequency as for the market risk standardized approach. In addition, banks using the SA-CVA must have the ability to produce SA-CVA capital requirement calculations at the request of SAMA and must accordingly provide the calculations.
11.29. The SA-CVA uses as inputs the sensitivities of regulatory CVA to counterparty credit spreads and market risk factors driving the values of covered transactions. Sensitivities must be computed by banks in accordance with the prudent valuation guidance set out in Basel Framework.
11.30. For a bank to be considered eligible for the use of SA-CVA by SAMA as set out in 11.7 of this framework, the bank must meet the following criteria at the minimum.
(1) A bank must be able to model exposure and calculate, on at least a monthly basis, CVA and CVA sensitivities to the market risk factors specified in 11.54 to 11.77 in this framework.
(2) A bank must have a CVA desk (or a similar dedicated function) responsible for risk management and hedging of CVA.
Regulatory CVA Calculations
11.31. A bank must calculate regulatory CVA for each counterparty with which it has at least one covered position for the purpose of the CVA risk capital requirements.
11.32. Regulatory CVA at a counterparty level must be calculated according to the following principles. A bank must demonstrate its compliance to the principles to SAMA.
(1) Regulatory CVA must be calculated as the expectation of future losses resulting from default of the counterparty under the assumption that the bank itself is free from the default risk. In expressing the regulatory CVA, non-zero losses must have a positive sign. This is reflected in 11.52 where WSkhdg must be subtracted from WSkCVA.
(2) The calculation must be based on at least the following three sets of inputs:
a) term structure of market-implied probability of default (PD);
b) market-consensus expected loss given default (ELGD);
c) simulated paths of discounted future exposure.
(3) The term structure of market-implied PD must be estimated from credit spreads observed in the markets. For counterparties whose credit is not actively traded (i.e. illiquid counterparties), the market-implied PD must be estimated from proxy credit spreads estimated for these counterparties according to the following requirements:
a) A bank must estimate the credit spread curves of illiquid counterparties from credit spreads observed in the markets of the counterparty's liquid peers via an algorithm that discriminates on at least the following three variables: a measure of credit quality (e.g. rating), industry, and region.
b) In certain cases, mapping an illiquid counterparty to a single liquid reference name can be allowed. A typical example would be mapping a municipality to its home country (i.e. setting the municipality credit spread equal to the sovereign credit spread plus a premium). A bank must justify to SAMA each case of mapping an illiquid counterparty to a single liquid reference name
c) When no credit spreads of any of the counterparty's peers is available due to the counterparty's specific type (e.g. project finance, funds), a bank is allowed to use a more fundamental analysis of credit risk to proxy the spread of an illiquid counterparty. However, where historical PDs are used as part of this assessment, the resulting spread cannot be based on historical PD only - it must relate to credit markets.
(4) The market-consensus ELGD value must be the same as the one used to calculate the risk-neutral PD from credit spreads unless the bank can demonstrate that the seniority of the exposure resulting from covered positions differs from the seniority of senior unsecured bonds. Collateral provided by the counterparty does not change the seniority of the exposure.
(5) The simulated paths of discounted future exposure are produced by pricing all derivative transactions with the counterparty along simulated paths of relevant market risk factors and discounting the prices to today using risk-free interest rates along the path.
(6) All market risk factors material for the transactions with a counterparty must be simulated as stochastic processes for an appropriate number of paths defined on an appropriate set of future time points extending to the maturity of the longest transaction.
(7) For transactions with a significant level of dependence between exposure and the counterparty's credit quality, this dependence should be taken into account.
(8) For margined counterparties, collateral is permitted to be recognized as a risk mitigant under the following conditions:
a) Collateral management requirements outlined in7.39 and 7.40 in this framework are satisfied.
b) All documentation used in collateralized transactions must be binding on all parties and legally enforceable in all relevant jurisdictions. Banks must have conducted sufficient legal review to verify this and have a well founded legal basis to reach this conclusion, and undertake such further review as necessary to ensure continuing enforceability.
(9) For margined counterparties, the simulated paths of discounted future exposure must capture the effects of margining collateral that is recognized as a risk mitigant along each exposure path. All the relevant contractual features such as the nature of the margin agreement (unilateral vs bilateral), the frequency of margin calls, the type of collateral, thresholds, independent amounts, initial margins and minimum transfer amounts must be appropriately captured by the exposure model. To determine collateral available to a bank at a given exposure measurement time point, the exposure model must assume that the counterparty will not post or return any collateral within a certain time period immediately prior to that time point. The assumed value of this time period, known as the margin period of risk (MPoR), cannot be less than SAMA's supervisory floor. For SFTs and client cleared transactions as specified in 8.12 in this framework, the supervisory floor for the MPoR is equal to 4+N business days, where N is the re-margining period specified in the margin agreement (in particular, for margin agreements with daily or intra-daily exchange of margin, the minimum MPoR is 5 business days). For all other transactions, the supervisory floor for the MPoR is equal to 9+N business days.
11.33. The simulated paths of discounted future exposure are obtained via the exposure models used by a bank for calculating front office/accounting CVA, adjusted (if needed) to meet the requirements imposed for regulatory CVA calculation. Model calibration process (with the exception of the MPoR), market and transaction data used for regulatory CVA calculation must be the same as the ones used for accounting CVA calculation.
11.34. The generation of market risk factor paths underlying the exposure models must satisfy and a bank must demonstrate to SAMA its compliance to the following requirements:
(1) Drifts of risk factors must be consistent with a risk-neutral probability measure. Historical calibration of drifts is not allowed.
(2) The volatilities and correlations of market risk factors must be calibrated to market data whenever sufficient data exist in a given market. Otherwise, historical calibration is permissible.
(3) The distribution of modelled risk factors must account for the possible non-normality of the distribution of exposures, including the existence of leptokurtosis (“fat tails”), where appropriate.
11.35. Netting recognition is the same as in the accounting CVA calculations. In particular, netting uncertainty can be modelled.
11.36. A bank must satisfy and demonstrate to SAMA its compliance to the following requirements:
(1) Exposure models used for calculating regulatory CVA must be part of a CVA risk management framework that includes the identification, measurement, management, approval and internal reporting of CVA risk. A bank must have a credible track record in using these exposure models for calculating CVA and CVA sensitivities to market risk factors.
(2) Senior management should be actively involved in the risk control process and must regard CVA risk control as an essential aspect of the business to which significant resources need to be devoted.
(3) A bank must have a process in place for ensuring compliance with a documented set of internal policies, controls and procedures concerning the operation of the exposure system used for accounting CVA calculations.
(4) A bank must have an independent control unit that is responsible for the effective initial and ongoing validation of the exposure models. This unit must be independent from business credit and trading units (including the CVA desk), must be adequately staffed and must report directly to senior management of the bank.
(5) A bank must document the process for initial and ongoing validation of its exposure models to a level of detail that would enable a third party to understand how the models operate, their limitations, and their key assumptions; and recreate the analysis. This documentation must set out the minimum frequency with which ongoing validation will be conducted as well as other circumstances (such as a sudden change in market behavior) under which additional validation should be conducted. In addition, the documentation must describe how the validation is conducted with respect to data flows and portfolios, what analyses are used and how representative counterparty portfolios are constructed.
(6) The pricing models used to calculate exposure for a given path of market risk factors must be tested against appropriate independent benchmarks for a wide range of market states as part of the initial and ongoing model validation process. Pricing models for options must account for the nonlinearity of option value with respect to market risk factors.
(7) An independent review of the overall CVA risk management process should be carried out regularly in the bank's own internal auditing process. This review should include both the activities of the CVA desk and of the independent risk control unit.
(8) A bank must define criteria on which to assess the exposure models and their inputs and have a written policy in place to describe the process to assess the performance of exposure models and remedy unacceptable performance.
(9) Exposure models must capture transaction-specific information in order to aggregate exposures at the level of the netting set. A bank must verify that transactions are assigned to the appropriate netting set within the model.
(10) Exposure models must reflect transaction terms and specifications in a timely, complete, and conservative fashion. The terms and specifications must reside in a secure database that is subject to formal and periodic audit. The transmission of transaction terms and specifications data to the exposure model must also be subject to internal audit, and formal reconciliation processes must be in place between the internal model and source data systems to verify on an ongoing basis that transaction terms and specifications are being reflected in the exposure system correctly or at least conservatively.
(11) The current and historical market data must be acquired independently of the lines of business and be compliant with accounting. They must be fed into the exposure models in a timely and complete fashion, and maintained in a secure database subject to formal and periodic audit. A bank must also have a well-developed data integrity process to handle the data of erroneous and/or anomalous observations. In the case where an exposure model relies on proxy market data, a bank must set internal policies to identify suitable proxies and the bank must demonstrate empirically on an ongoing basis that the proxy provides a conservative representation of the underlying risk under adverse market conditions.
Eligible hedges
11.37. Only whole transactions that are used for the purpose of mitigating CVA risk, and managed as such, can be eligible hedges. Transactions cannot be split into several effective transactions.
11.38. Eligible hedges can include:
(1) instruments that hedge variability of the counterparty credit spread; and
(2) instruments that hedge variability of the exposure component of CVA risk.
11.39. Instruments that are not eligible for the internal models approach for market risk under Chapter 10 to Chapter 13 of the Minimum Capital Requirements for Market Risk (e.g. tranched credit derivatives) cannot be eligible CVA hedges.
Multiplier
11.40. Aggregated capital requirements can be scaled up by the multiplier mCVA.
11.41. The multiplier mCVA is set at 1. SAMA may require a bank to use a higher value of mCVA if SAMA determines that the bank’s CVA model risk warrants it (e.g. if the level of model risk for the calculation of CVA sensitivities is too high or the dependence between the bank’s exposure to a counterparty and the counterparty’s credit quality is not appropriately taken into account in its CVA calculations).
Calculations
11.42. The SA-CVA capital requirements are calculated as the sum of the capital requirements for delta and vega risks calculated for the entire CVA portfolio (including eligible hedges).
11.43. The capital requirements for delta risk are calculated as the simple sum of delta capital requirements calculated independently for the following six risk classes:
(1) interest rate risk;
(2) foreign exchange (FX) risk;
(3) counterparty credit spread risk;
(4) reference credit spread risk (i.e. credit spreads that drive the CVA exposure component);
(5) equity risk; and
(6) commodity risk.
11.44. If an instrument is deemed as an eligible hedge for credit spread delta risk, it must be assigned in its entirety (see 11.37 of this framework) either to the counterparty credit spread or to the reference credit spread risk class. Instruments must not be split between the two risk classes.
11.45. The capital requirements for vega risk are calculated as the simple sum of vega capital requirements calculated independently for the following five risk classes. There is no vega capital requirements for counterparty credit spread risk.
(1) interest rate risk; (IR);
(2) FX risk;
(3) reference credit spread risk;
(4) equity risk; and
(5) commodity risk
11.46. Delta and vega capital requirements are calculated in the same manner using the same procedures set out in 11.47 to 11.53 of this framework.
11.47. For each risk class, (i) the sensitivity of the aggregate CVA, skCVA, and (ii) the sensitivity of the market value of all eligible hedging instruments in the CVA portfolio, skHdg, to each risk factor k in the risk class are calculated. The sensitivities are defined as the ratio of the change of the value in question (i.e. (i) aggregate CVA or (ii) market value of all CVA hedges) caused by a small change of the risk factor’s current value to the size of the change. Specific definitions for each risk class are set out in 11.54 to 11.77of this framework. These definitions include specific values of changes or shifts in risk factors. However, a bank may use smaller values of risk factor shifts if doing so is consistent with internal risk management calculations. A bank may use AAD and similar computational techniques to calculate CVA sensitivities under the SA-CVA if doing so is consistent with the bank’s internal risk management calculations and the relevant validation standards described in the SA-CVA framework.
11.48. CVA sensitivities for vega risk are always material and must be calculated regardless of whether or not the portfolio includes options. When CVA sensitivities for vega risk are calculated, the volatility shift must apply to both types of volatilities that appear in exposure models:
(1) volatilities used for generating risk factor paths; and
(2) volatilities used for pricing options.
11.49. If a hedging instrument is an index, its sensitivities to all risk factors upon which the value of the index depends must be calculated. The index sensitivity to risk factor k must be calculated by applying the shift of risk factor k to all index constituents that depend on this risk factor and recalculating the changed value of the index. For example, to calculate delta sensitivity of S&P500 to large financial companies, a bank must apply the relevant shift to equity prices of all large financial companies that are constituents of S&P500 and re-compute the index.
11.50. For the following risk classes, a bank may choose to introduce a set of additional risk factors that directly correspond to qualified credit and equity indices. For delta risks, a credit or equity index is qualified if it satisfies liquidity and diversification conditions specified in Chapter 7.31 of the Minimum Capital Requirements for Market Risk; for vega risks, any credit or equity index is qualified. Under this option, a bank must calculate sensitivities of CVA and the eligible CVA hedges to the qualified index risk factors in addition to sensitivities to the non-index risk factors. Under this option, for a covered transaction or an eligible hedging instrument whose underlying is a qualified index, its contribution to sensitivities to the index constituents is replaced with its contribution to a single sensitivity to the underlying index. For example, for a portfolio consisting only of equity derivatives referencing only qualified equity indices, no calculation of CVA sensitivities to non-index equity risk factors is necessary. If more than 75% of constituents of a qualified index (taking into account the weightings of the constituents) are mapped to the same sector, the entire index must be mapped to that sector and treated as a single-name sensitivity in that bucket. In all other cases, the sensitivity must be mapped to the applicable index bucket.
(1) counterparty credit spread risk;
(2) reference credit spread risk; and
(3) equity risk.
11.51. The weighted sensitivities WSkCVA and WSkHdg for each risk factor k are calculated by multiplying the net sensitivities SkCVA and SkHdg, respectively, by the corresponding risk weight RWk (the risk weights applicable to each risk class are specified in 11.54 to 11.77 of this framework).
WSkCVA = RWkskCVA
WSkHdg = RWkskHdg
11.52. The net weighted sensitivity of the CVA portfolio Sk to risk factor k is obtained by44:
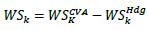
11.53. For each risk class, the net sensitivities are aggregated as follows:
(1) The weighted sensitivities must be aggregated into a capital requirement Kb within each bucket b (the buckets and correlation parameters ρKl applicable to each risk class are specified in 11.54 to 11.77 of this framework), where R is the hedging disallowance parameter, set at 0.01, that prevents the possibility of recognizing perfect hedging of CVA risk.
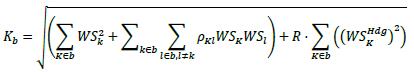
(2) Bucket-level capital requirements must then be aggregated across buckets within each risk class (the correlation parameters γbc applicable to each risk class are specified in 11.54 to 11.77 of this framework). Note that this equation differs from the corresponding aggregation equation for market risk capital requirements in Chapter 7.4 of the Minimum Capital Requirements for Market Risk, including the multiplier mCVA.
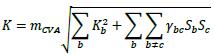
(3) In calculating K in above (2), S is defined as the sum of the weighted b sensitivities WS for all risk factors k within bucket b, floored by -K and k b capped by K, and the S is defined in the same way for all risk factors k in b c bucket c:
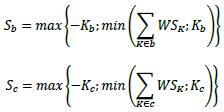
Interest rates buckets, risk factors, sensitivities, risk weights and correlations
11.54. For interest rate delta and vega risks, buckets must be set per individual currencies.
11.55. For interest rate delta and vega risks, cross-bucket correlation γbc is set at 0.5 for all currency pairs.
11.56. The interest rate delta risk factors for a bank’s reporting currency and for the following currencies USD, EUR, GBP, AUD, CAD, SEK or JPY:
(1) The interest rate delta risk factors are the absolute changes of the inflation rate and of the risk-free yields for the following five tenors: 1 year, 2 years, 5 years, 10 years and 30 years.
(2) The sensitivities to the abovementioned risk-free yields are measured by changing the risk-free yield for a given tenor for all curves in a given currency by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001. The sensitivity to the inflation rate is obtained by changing the inflation rate by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.
(3) The risk weights RWk are set as follows:
Table 3: Risk weight for interest rate risk (specified currencies) Risk factor 1 year 2 years 5 years 10 years 30 years Inflation Risk weight 1.11% 0.93% 0.74% 0.74% 0.74% 1.11% (4) The correlations between pairs of risk factors ρkl are set as follows:
Table 4: Correlations for interest rate risk factors (specified currencies) 1 year 2 years 5 years 10 years 30 years Inflation 1 year 100% 91% 72% 55% 31% 40% 2 years 100% 87% 72% 45% 40% 5 years 100% 91% 68% 40% 10 years 100% 83% 40% 30 years 100% 40% Inflation 100% 11.57. The interest rate delta risk factors for other currencies not specified in 11.56 of this framework:
(1) The interest rate risk factors are the absolute change of the inflation rate and the parallel shift of the entire risk-free yield curve for a given currency.
(2) The sensitivity to the yield curve is measured by applying a parallel shift to all risk-free yield curves in a given currency by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001. The sensitivity to the inflation rate is obtained by changing the inflation rate by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.
(3) The risk weights for both the risk-free yield curve and the inflation rate RWk are set at 1.85%.
(4) The correlations between the risk-free yield curve and the inflation rate ρKl are set at 40%.
11.58. The interest rate vega risk factors for all currencies:
(1) The interest rate vega risk factors are a simultaneous relative change of all volatilities for the inflation rate and a simultaneous relative change of all interest rate volatilities for a given currency.
(2) The sensitivity to (i) the interest rate volatilities or (ii) inflation rate volatilities is measured by respectively applying a simultaneous shift to (i) all interest rate volatilities or (ii) inflation rate volatilities by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) The risk weights for both the interest rate volatilities and the inflation rate volatilities RWk are set to 100%.
(4) Correlations between the interest rate volatilities and the inflation rate volatilities ρKl are set at 40%.
Foreign exchange buckets, risk factors, sensitivities, risk weights and correlations
11.59. For FX delta and vega risks, buckets must be set per individual currencies except for a bank’s own reporting currency.
11.60. For FX delta and vega risks, the cross-bucket correlation γbc is set at 06. for all currency pairs.
11.61. The FX delta risk factors for all currencies:
(1) The single FX delta risk factor is defined as the relative change of the FX spot rate between a given currency and a bank’s reporting currency, where the FX spot rate is the current market price of one unit of another currency expressed in the units of the bank’s reporting currency.
(2) Sensitivities to FX spot rates are measured by shifting the exchange rate between the bank’s reporting currency and another currency (i.e. the value of one unit of another currency expressed in units of the reporting currency) by 1% relative to its current value and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01. For transactions that reference an exchange rate between a pair of non-reporting currencies, the sensitivities to the FX spot rates between the bank’s reporting currency and each of the referenced non-reporting currencies must be measured.45
(3) The risk weights for all exchange rates between the bank’s reporting currency and another currency are set at 11%.
11.62. The FX vega risk factors for all currency:
(1) The single FX vega risk factor is a simultaneous relative change of all volatilities for an exchange rate between a bank’s reporting currency and another given currency.
(2) The sensitivities to the FX volatilities are measured by simultaneously shifting all volatilities for a given exchange rate between the bank’s reporting currency and another currency by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01. For transactions that reference an exchange rate between a pair of non-reporting currencies, the volatilities of the FX spot rates between the bank’s reporting currency and each of the referenced non-reporting currencies must be measured.
(3) The risk weights for FX volatilities RWk are set to 100%.
Counterparty credit spread buckets, risk factors, sensitivities, risk weights and correlations
11.63. Counterparty credit spread risk is not subject to vega risk capital requirements. Buckets for delta risk are set as follows:
(1) Buckets 1 to 7 are defined for factors that are not qualified indices as set out in 11.50 of this framework;
(2) Bucket 8 is set for the optional treatment of qualified indices. Under the optional treatment, only instruments that reference qualified indices can be assigned to bucket 8, while all single-name and all non-qualified index hedges must be assigned to buckets 1 to 7 for calculations of CVA sensitivities and sensitivities. For any instrument referencing an index assigned to buckets 1 to 7, the look-through approach must be used (i.e., sensitivity of the hedge to each index constituent must be calculated).
Table 5: Buckets for counterparty credit spread delta risk Bucket number Sector 1 a) Sovereigns including central banks, multilateral development banks b) Local government, government-backed non-financials, education and public administration 2 Financials including government-backed financials 3 Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying 4 Consumer goods and services, transportation and storage, administrative and support service activities 5 Technology, telecommunications 6 Health care, utilities, professional and technical activities 7 Other sector 8 Qualified Indices 11.64. For counterparty credit spread delta risk, cross-bucket correlations γbc are set as follows:
Table 6: Cross-bucket correlations for counterparty credit spread delta risk Bucket 1 2 3 4 5 6 7 8 1 100% 10% 20% 25% 20% 15% 0% 45% 2 100% 5% 15% 20% 5% 0% 45% 3 100% 20% 25% 5% 0% 45% 4 100% 25% 5% 0% 45% 5 100% 5% 0% 45% 6 100% 0% 45% 7 100% 0% 8 100% 11.65. The counterparty credit spread delta risk factors for a given bucket:
(1) The counterparty credit spread delta risk factors are absolute shifts of credit spreads of individual entities (counterparties and reference names for counterparty credit spread hedges) and qualified indices (if the optional treatment is chosen) for the following tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(2) For each entity and each tenor point, the sensitivities are measured by shifting the relevant credit spread by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.
(3) The risk weights RWk are set as follows the depending on the entity's bucket, where IG, HY, and NR represent “investment grade”, “high yield” and “not rated” as specified for the BA-CVA in 11.16 of this framework. The same risk weight for a given bucket and given credit quality applies to all tenors.
Table 7: Risk weights for counterparty credit spread delta risk Bucket 1 a) 1 b) 2 3 4 5 6 7 8 IG names 0.5% 1.0% 5.0% 3.0% 3.0% 2.0% 1.5% 5.0% 1.5% HY and NR names 2.0% 4.0% 12.0% 7.0% 8.5% 5.5% 5.0% 12.0% 5.0% (4) For buckets 1 to 7, the correlation parameter ρkl between two weighted sensitivities WSk and WSi is calculated as follows, where:
a) ρtenor is equal to 100% if the two tenors are the same and 90% otherwise;
b) ρname is equal to 100% if the two names are the same, 90% if the two names are distinct, but legally related and 50% otherwise;
c) ρquality is equal to 100% if the credit quality of the two names is the same (i.e. IG and IG or HY/NR and HY/NR) and 80% otherwise.
ρkl = ρtenor ∙ ρname ∙ ρquality
(5) For bucket 8, the correlation parameter ρkl between two weighted sensitivities WSk and WSi is calculated as follows, where
a) ρtenor is equal to 100% if the two tenors are the same and 90% otherwise;
b) ρname is equal to 100% if the two indices are the same and of the same series, 90% if the two indices are the same, but of distinct series, and 80% otherwise;
c) ρquality is equal to 100% if the credit quality of the two indices is the same (ie IG and IG or HY and HY) and 80% otherwise.
ρkl = ρtenor ∙ ρname ∙ ρquality
Reference credit spread buckets, risk factors, sensitivities, risk weights and correlations
11.66. Reference credit spread risk is subject to both delta and vega risk capital requirements. Buckets for delta and vega risks are set as follows, where IG, HY and NR represent “investment grade”, “high yield” and “not rated” as specified for the BA-CVA in 11.16 of this framework:
Table 8: Buckets for reference credit spread risk Bucket number Credit quality Sector 1 IG Sovereigns including central banks, multilateral development banks 2 Local government, government-backed non-financials, education and public administration 3 Financials including government-backed financials 4 Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying 5 Consumer goods and services, transportation and storage, administrative and support service activities 6 Technology, telecommunications 7 Health care, utilities, professional and technical activities 8 (HY) and NR Sovereigns including central banks, multilateral development banks 9 Local government, government-backed non-financials, education and public administration 10 Financials including government-backed financials 11 Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying 12 Consumer goods and services, transportation and storage, administrative and support service activities 13 Technology, telecommunications 14 Health care, utilities, professional and technical activities 15 (Not applicable) Other sector 16 IG Qualified Indices 17 HY Qualified Indices 11.67. For reference credit spread delta and Vega risks, cross-bucket correlations γbc are set as follows:
(1) The cross-bucket correlations γbc between buckets of the same credit quality (ie either IG or HY/NR) are set as follows:
Table 9: Cross-bucket correlations for reference credit spread risk Bucket 1/8 2/9 3/10 4/11 5/12 6/13 7/14 15 16 17 1/8 100% 75% 10% 20% 25% 20% 15% 0% 45% 45% 2/9 100% 5% 15% 20% 15% 10% 0% 45% 45% 3/10 100% 5% 15% 20% 5% 0% 45% 45% 4/11 100% 20% 25% 5% 0% 45% 45% 5/12 100% 25% 5% 0% 45% 45% 6/13 100% 5% 0% 45% 45% 7/14 100% 0% 45% 45% 15 100% 0% 0% 16 100% 75% 17 100% (2) For cross-bucket correlations γbc between buckets 1 to 14 of different credit quality (i.e. IG and HY/NR), the correlations γbc specified in 11.67 of this framework (1) are divided by 2.
11.68. Reference credit spread delta risk factors for a given bucket:
(1) The single reference credit spread delta risk factor is a simultaneous absolute shift of the credit spreads of all tenors for all reference names in the bucket.
(2) The sensitivity to reference credit spread delta risk is measured by simultaneously shifting the credit spreads of all tenors for all reference names in the bucket by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.
(3) The risk weights RWk are set as follows depending on the reference name's bucket:
Table 10: Risk weights for reference credit spread delta risk IG bucket 1 2 3 4 5 6 7 8 9 Risk weigh 0.5% 1.0% 5.0% 3.0% 3.0% 2.0% 1.5% 2.0% 4.0% HY/NR bucket 10 11 12 13 14 15 16 17 Risk weight 12.0% 7.0% 8.5% 5.5% 5.0% 12.0% 1.5% 5.0% 11.69. Reference credit spread vega risk factors for a given bucket:
(1) The single reference credit spread Vega risk factor is a simultaneous relative shift of the volatilities of credit spreads of all tenors for all reference names in the bucket.
(2) The sensitivity to the reference credit spread vega risk factor is measured by simultaneously shifting the volatilities of credit spreads of all tenors for all reference names in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) Risk weights for reference credit spread volatilities ??? are set to 100%.
Equity buckets, risk factors, sensitivities, risk weights and correlations
11.70. For equity delta and vega risks, buckets are set as follow, where:
(1) Market capitalization (“market cap”) is defined as the sum of the market capitalizations of the same legal entity or group of legal entities across all stock markets globally. The reference to “group of legal entities” covers cases where the listed entity is a parent company of a group of legal entities. Under no circumstances should the sum of the market capitalizations of multiple related listed entities be used to determine whether a listed entity is “large market cap” or “small market cap”.
(2) “Large market cap” is defined as a market capitalization equal to or greater than USD 2 billion and “small market cap” is defined as a market capitalization of less than USD 2 billion.
(3) The advanced economies are Canada, the United States, Mexico, the euro area, the non-euro area western European countries (the United Kingdom, Norway, Sweden, Denmark and Switzerland), Japan, Oceania (Australia and New Zealand), Singapore and Hong Kong SAR.
(4) To assign a risk exposure to a sector, banks must rely on a classification that is commonly used in the market for grouping issuers by industry sector. The bank must assign each issuer to one of the sector buckets in the table above and it must assign all issuers from the same industry to the same sector. Risk positions from any issuer that a bank cannot assign to a sector in this fashion must be assigned to the “other sector” (i.e. bucket 11). For multinational multi-sector equity issuers, the allocation to a particular bucket must be done according to the most material region and sector in which the issuer operates.
Table 11: Buckets for equity risk Bucket number Size Region Sector 1 Large Emerging market economies Consumer goods and services, transportation and storage, administrative and support service activities, healthcare, utilities 2 Telecommunications, industrials 3 Basic materials, energy, agriculture, manufacturing, mining and quarrying 4 Financials including government-backed financials, real estate activities, technology 5 Advanced economies Consumer goods and services, transportation and storage, administrative and support service activities, healthcare, utilities 6 Telecommunications, industrials 7 Basic materials, energy, agriculture, manufacturing, mining and quarrying 8 Financials including government-backed financials, real estate activities, technology 9 Small Emerging market economies All sectors described under bucket numbers 1, 2, 3, and 4 10 Advanced economies All sectors described under bucket numbers 5, 6, 7, and 8 11 (Not applicable) Other sector 12 Large cap, advanced economies Qualified Indices 13 Other Qualified Indices 11.71. For equity delta and vega risks, cross-bucket correlation γbc is set at 15% for all cross-bucket pairs that fall within bucket numbers 1 to 10. The cross-bucket correlation between buckets 12 and 13 is set at 75% and the cross bucket correlation between buckets 12 or 13 and any of the buckets 1-10 is 45%. γbc is set at 0% for all cross-bucket pairs that include bucket 11.
11.72. Equity delta risk factors for a given bucket:
(1) The single equity delta risk factor is a simultaneous relative shift of equity spot prices for all reference names in the bucket.
(2) The sensitivity to the equity delta risk factors is measured by simultaneously shifting the equity spot prices for all reference names in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) Risk weights RWk are set as follows depending on the reference name's bucket:
Table 12: Risk weights for equity delta risk Bucket number Risk weight 1 55% 2 60% 3 45% 4 55% 5 30% 6 35% 7 40% 8 50% 9 70% 10 50% 11 70% 12 15% 13 25% 11.73. Equity Vega risk factors for a given bucket:
(1) The single equity vega risk factor is a simultaneous relative shift of the volatilities for all reference names in the bucket.
(2) The sensitivity to equity vega risk factors are measured by simultaneously shifting the volatilities for all reference names in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) The risk weights for equity volatilities RWk are set to 78% for large market capitalization buckets and to 100% for other buckets.
Commodity buckets, risk factors, sensitivities, risk weights and correlations
11.74. For commodity delta and vega risks, buckets are set as follows:
Table 13: Buckets for commodity risk Bucket number Commodity group Examples 1 Energy – Solid combustibles coal, charcoal, wood pellets, nuclear fuel (such as uranium) 2 Energy – Liquid combustibles crude oil (such as Light-sweet, heavy, WTI and Brent); biofuels (such as bioethanol and biodiesel); petrochemicals (such as propane, ethane, gasoline, methanol and butane); refined fuels (such as jet fuel, kerosene, gasoil, fuel oil, naptha, heating oil and diesel) 3 Energy – Electricity and carbon trading electricity (such as spot, day-ahead, peak and off-peak); carbon emissions trading (such as certified emissions reductions, in delivery month EUA, RGGI CO2 allowance and renewable energy certificates) 4 Freight dry-bulk route (such as capesize, panamex, handysize and supramax); liquid-bulk/gas shipping route (such as suezmax, aframax and very large crude carriers) 5 Metals – nonprecious base metal (such as aluminum, copper, lead, nickel, tin and zinc); steel raw materials (such as steel billet, steel wire, steel coil, steel scrap and steel rebar, iron ore, tungsten, vanadium, titanium and tantalum); minor metals (such as cobalt, manganese, molybdenum) 6 Gaseous combustibles natural gas; liquefied natural gas 7 Precious metals (including gold) gold; silver; platinum; palladium 8 Grains & oilseed corn; wheat; soybean (such as soybean seed, soybean oil and soybean meal); oats; palm oil; canola; barley; rapeseed (such as rapeseed seed, rapeseed oil, and rapeseed meal); red bean, sorghum; coconut oil; olive oil; peanut oil; sunflower oil; rice 9 Livestock & dairy cattle (such live and feeder); poultry; lamb; fish; shrimp; dairy (such as milk, whey, eggs, butter and cheese) 10 Softs and other agriculturals cocoa; coffee (such as arabica and robusta); tea; citrus and orange juice; potatoes; sugar; cotton; wool; lumber and pulp; rubber 11 Other commodity industrial minerals (such as potash, fertilizer and phosphate rocks), rare earths; terephthalic acid; flat glass 11.75. For commodity delta and vega risks, cross-bucket correlation γbc is set at 20% for all cross-bucket pairs that fall within bucket numbers 1 to 10. γbc is set at 0% for all cross-bucket pairs that include bucket 11.
11.76. Commodity delta risk factors for a given bucket:
(1) The single commodity delta risk factor is a simultaneous relative shift of commodity spot prices for all commodities in the bucket.
(2) The sensitivities to commodity delta risk factors are measured by shifting the spot prices of all commodities in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) The risk weights RWk are set as follows depending on the reference name's bucket:
Table 14: Risk weights for commodity delta risk Bucket 1 2 3 4 5 6 7 8 9 10 11 RW 30% 35% 60% 80% 40% 45% 20% 35% 25% 35% 50% 11.77. Commodity vega risk factors for a given bucket:
(1) The single commodity vega risk factor is a simultaneous relative shift of the volatilities for all commodities in the bucket.
(2) The sensitivity to commodity vega risk factors is measured by simultaneously shifting the volatilities for all commodities in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) Risk weights for commodity volatilities RWk are set to 100%.
44 Note that the formula in 11.52 is set out under the convention that the CVA is positive as specified in 11.32 (1). It intends to recognize the risk reducing effect of hedging. For example, when hedging the counterparty credit spread component of CVA risk for a specific counterparty by buying credit protection on the counterparty: if the counterparty’s credit spread widens, the CVA (expressed as a positive value) increases resulting in the positive CVA sensitivity to the counterparty credit spread. At the same time, as the value of the hedge from the bank’s perspective increases as well (as credit protection becomes more valuable), the sensitivity of the hedge is also positive. The positive weighted sensitivities of the CVA and its hedge offset each other using the formula with the minus sign. If CVA loss had been expressed as a negative value, the minus sign in 11.52 would have been replaced by a plus sign.
45 For example, if a SAR-reporting bank holds an instrument that references the USD-GBP exchange rate, the bank must measure CVA sensitivity both to the SAR-GBP exchange rate and to the SAR- USD exchange rate.