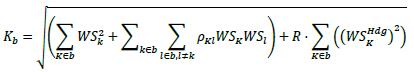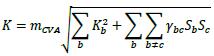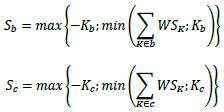Calculations

No: 44047144

Date(g): 27/12/2022 | Date(h): 4/6/1444

Status: In-Force

11.42.

The SA-CVA capital requirements are calculated as the sum of the capital requirements for delta and vega risks calculated for the entire CVA portfolio (including eligible hedges).

11.43.

The capital requirements for delta risk are calculated as the simple sum of delta capital requirements calculated independently for the following six risk classes:

(1)

interest rate risk;

(2)

foreign exchange (FX) risk;

(3)

counterparty credit spread risk;

(4)

reference credit spread risk (i.e. credit spreads that drive the CVA exposure component);

(5)

equity risk; and

(6)

commodity risk.

11.44.

If an instrument is deemed as an eligible hedge for credit spread delta risk, it must be assigned in its entirety (see 11.37 of this framework) either to the counterparty credit spread or to the reference credit spread risk class. Instruments must not be split between the two risk classes.

11.45.

The capital requirements for vega risk are calculated as the simple sum of vega capital requirements calculated independently for the following five risk classes. There is no vega capital requirements for counterparty credit spread risk.

(1)

interest rate risk; (IR);

(2)

FX risk;

(3)

reference credit spread risk;

(4)

equity risk; and

(5)

commodity risk

11.46.

Delta and vega capital requirements are calculated in the same manner using the same procedures set out in 11.47 to 11.53 of this framework.

11.47.

For each risk class, (i) the sensitivity of the aggregate CVA, s_k^CVA, and (ii) the sensitivity of the market value of all eligible hedging instruments in the CVA portfolio, s_k^Hdg, to each risk factor k in the risk class are calculated. The sensitivities are defined as the ratio of the change of the value in question (i.e. (i) aggregate CVA or (ii) market value of all CVA hedges) caused by a small change of the risk factor’s current value to the size of the change. Specific definitions for each risk class are set out in 11.54 to 11.77of this framework. These definitions include specific values of changes or shifts in risk factors. However, a bank may use smaller values of risk factor shifts if doing so is consistent with internal risk management calculations. A bank may use AAD and similar computational techniques to calculate CVA sensitivities under the SA-CVA if doing so is consistent with the bank’s internal risk management calculations and the relevant validation standards described in the SA-CVA framework.

11.48.

CVA sensitivities for vega risk are always material and must be calculated regardless of whether or not the portfolio includes options. When CVA sensitivities for vega risk are calculated, the volatility shift must apply to both types of volatilities that appear in exposure models:

(1)

volatilities used for generating risk factor paths; and

(2)

volatilities used for pricing options.

11.49.

If a hedging instrument is an index, its sensitivities to all risk factors upon which the value of the index depends must be calculated. The index sensitivity to risk factor k must be calculated by applying the shift of risk factor k to all index constituents that depend on this risk factor and recalculating the changed value of the index. For example, to calculate delta sensitivity of S&P500 to large financial companies, a bank must apply the relevant shift to equity prices of all large financial companies that are constituents of S&P500 and re-compute the index.

11.50.

For the following risk classes, a bank may choose to introduce a set of additional risk factors that directly correspond to qualified credit and equity indices. For delta risks, a credit or equity index is qualified if it satisfies liquidity and diversification conditions specified in Chapter 7.31 of the Minimum Capital Requirements for Market Risk; for vega risks, any credit or equity index is qualified. Under this option, a bank must calculate sensitivities of CVA and the eligible CVA hedges to the qualified index risk factors in addition to sensitivities to the non-index risk factors. Under this option, for a covered transaction or an eligible hedging instrument whose underlying is a qualified index, its contribution to sensitivities to the index constituents is replaced with its contribution to a single sensitivity to the underlying index. For example, for a portfolio consisting only of equity derivatives referencing only qualified equity indices, no calculation of CVA sensitivities to non-index equity risk factors is necessary. If more than 75% of constituents of a qualified index (taking into account the weightings of the constituents) are mapped to the same sector, the entire index must be mapped to that sector and treated as a single-name sensitivity in that bucket. In all other cases, the sensitivity must be mapped to the applicable index bucket.

(1)

counterparty credit spread risk;

(2)

reference credit spread risk; and

(3)

equity risk.

11.51.

The weighted sensitivities WS_k^CVA and WS_k^Hdg for each risk factor k are calculated by multiplying the net sensitivities S_k^CVA and S_k^Hdg, respectively, by the corresponding risk weight RW_k (the risk weights applicable to each risk class are specified in 11.54 to 11.77 of this framework).

WS_k^CVA = RW_ks_k^CVA

WS_k^Hdg = RW_ks_k^Hdg

11.52.

The net weighted sensitivity of the CVA portfolio S_k to risk factor k is obtained by⁴⁴:

11.53.

For each risk class, the net sensitivities are aggregated as follows:

(1)

The weighted sensitivities must be aggregated into a capital requirement K_b within each bucket b (the buckets and correlation parameters ρ_Kl applicable to each risk class are specified in 11.54 to 11.77 of this framework), where R is the hedging disallowance parameter, set at 0.01, that prevents the possibility of recognizing perfect hedging of CVA risk.

(2)

Bucket-level capital requirements must then be aggregated across buckets within each risk class (the correlation parameters γbc applicable to each risk class are specified in 11.54 to 11.77 of this framework). Note that this equation differs from the corresponding aggregation equation for market risk capital requirements in Chapter 7.4 of the Minimum Capital Requirements for Market Risk, including the multiplier m_CVA.

(3)

In calculating K in above (2), S is defined as the sum of the weighted b sensitivities WS for all risk factors k within bucket b, floored by -K and k b capped by K, and the S is defined in the same way for all risk factors k in b c bucket c:

Interest rates buckets, risk factors, sensitivities, risk weights and correlations

11.54.

For interest rate delta and vega risks, buckets must be set per individual currencies.

11.55.

For interest rate delta and vega risks, cross-bucket correlation γ_bc is set at 0.5 for all currency pairs.

11.56.

The interest rate delta risk factors for a bank’s reporting currency and for the following currencies USD, EUR, GBP, AUD, CAD, SEK or JPY:

(1)

The interest rate delta risk factors are the absolute changes of the inflation rate and of the risk-free yields for the following five tenors: 1 year, 2 years, 5 years, 10 years and 30 years.

(2)

The sensitivities to the abovementioned risk-free yields are measured by changing the risk-free yield for a given tenor for all curves in a given currency by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001. The sensitivity to the inflation rate is obtained by changing the inflation rate by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.

(3)

The risk weights RW_k are set as follows:

Table 3: Risk weight for interest rate risk (specified currencies)
Risk factor	1 year	2 years	5 years	10 years	30 years	Inflation
Risk weight	1.11%	0.93%	0.74%	0.74%	0.74%	1.11%

(4)

The correlations between pairs of risk factors ρ_kl are set as follows:

Table 4: Correlations for interest rate risk factors (specified currencies)
	1 year	2 years	5 years	10 years	30 years	Inflation
1 year	100%	91%	72%	55%	31%	40%
2 years		100%	87%	72%	45%	40%
5 years			100%	91%	68%	40%
10 years				100%	83%	40%
30 years					100%	40%
Inflation						100%

11.57.

The interest rate delta risk factors for other currencies not specified in 11.56 of this framework:

(1)

The interest rate risk factors are the absolute change of the inflation rate and the parallel shift of the entire risk-free yield curve for a given currency.

(2)

The sensitivity to the yield curve is measured by applying a parallel shift to all risk-free yield curves in a given currency by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001. The sensitivity to the inflation rate is obtained by changing the inflation rate by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.

(3)

The risk weights for both the risk-free yield curve and the inflation rate RW_k are set at 1.85%.

(4)

The correlations between the risk-free yield curve and the inflation rate ρ_Kl are set at 40%.

11.58.

The interest rate vega risk factors for all currencies:

(1)

The interest rate vega risk factors are a simultaneous relative change of all volatilities for the inflation rate and a simultaneous relative change of all interest rate volatilities for a given currency.

(2)

The sensitivity to (i) the interest rate volatilities or (ii) inflation rate volatilities is measured by respectively applying a simultaneous shift to (i) all interest rate volatilities or (ii) inflation rate volatilities by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.

(3)

The risk weights for both the interest rate volatilities and the inflation rate volatilities RW_k are set to 100%.

(4)

Correlations between the interest rate volatilities and the inflation rate volatilities ρ_Kl are set at 40%.

	Foreign exchange buckets, risk factors, sensitivities, risk weights and correlations
11.59.	For FX delta and vega risks, buckets must be set per individual currencies except for a bank’s own reporting currency.
11.60.	For FX delta and vega risks, the cross-bucket correlation γ_bc is set at 06. for all currency pairs.
11.61.	The FX delta risk factors for all currencies:
	(1)	The single FX delta risk factor is defined as the relative change of the FX spot rate between a given currency and a bank’s reporting currency, where the FX spot rate is the current market price of one unit of another currency expressed in the units of the bank’s reporting currency.
	(2)	Sensitivities to FX spot rates are measured by shifting the exchange rate between the bank’s reporting currency and another currency (i.e. the value of one unit of another currency expressed in units of the reporting currency) by 1% relative to its current value and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01. For transactions that reference an exchange rate between a pair of non-reporting currencies, the sensitivities to the FX spot rates between the bank’s reporting currency and each of the referenced non-reporting currencies must be measured.⁴⁵
	(3)	The risk weights for all exchange rates between the bank’s reporting currency and another currency are set at 11%.
11.62.	The FX vega risk factors for all currency:
	(1)	The single FX vega risk factor is a simultaneous relative change of all volatilities for an exchange rate between a bank’s reporting currency and another given currency.
	(2)	The sensitivities to the FX volatilities are measured by simultaneously shifting all volatilities for a given exchange rate between the bank’s reporting currency and another currency by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01. For transactions that reference an exchange rate between a pair of non-reporting currencies, the volatilities of the FX spot rates between the bank’s reporting currency and each of the referenced non-reporting currencies must be measured.
	(3)	The risk weights for FX volatilities RW_k are set to 100%.

Counterparty credit spread buckets, risk factors, sensitivities, risk weights and correlations

11.63.

Counterparty credit spread risk is not subject to vega risk capital requirements. Buckets for delta risk are set as follows:

(1)

Buckets 1 to 7 are defined for factors that are not qualified indices as set out in 11.50 of this framework;

(2)

Bucket 8 is set for the optional treatment of qualified indices. Under the optional treatment, only instruments that reference qualified indices can be assigned to bucket 8, while all single-name and all non-qualified index hedges must be assigned to buckets 1 to 7 for calculations of CVA sensitivities and sensitivities. For any instrument referencing an index assigned to buckets 1 to 7, the look-through approach must be used (i.e., sensitivity of the hedge to each index constituent must be calculated).

Table 5: Buckets for counterparty credit spread delta risk
Bucket number	Sector
1	a) Sovereigns including central banks, multilateral development banks
1	b) Local government, government-backed non-financials, education and public administration
2	Financials including government-backed financials
3	Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying
4	Consumer goods and services, transportation and storage, administrative and support service activities
5	Technology, telecommunications
6	Health care, utilities, professional and technical activities
7	Other sector
8	Qualified Indices

11.64.

For counterparty credit spread delta risk, cross-bucket correlations γ_bc are set as follows:

Table 6: Cross-bucket correlations for counterparty credit spread delta risk
Bucket	1	2	3	4	5	6	7	8
1	100%	10%	20%	25%	20%	15%	0%	45%
2		100%	5%	15%	20%	5%	0%	45%
3			100%	20%	25%	5%	0%	45%
4				100%	25%	5%	0%	45%
5					100%	5%	0%	45%
6						100%	0%	45%
7							100%	0%
8								100%

11.65.

The counterparty credit spread delta risk factors for a given bucket:

(1)

The counterparty credit spread delta risk factors are absolute shifts of credit spreads of individual entities (counterparties and reference names for counterparty credit spread hedges) and qualified indices (if the optional treatment is chosen) for the following tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.

(2)

For each entity and each tenor point, the sensitivities are measured by shifting the relevant credit spread by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.

(3)

The risk weights RW_k are set as follows the depending on the entity's bucket, where IG, HY, and NR represent “investment grade”, “high yield” and “not rated” as specified for the BA-CVA in 11.16 of this framework. The same risk weight for a given bucket and given credit quality applies to all tenors.

Table 7: Risk weights for counterparty credit spread delta risk
Bucket	1 a)	1 b)	2	3	4	5	6	7	8
IG names	0.5%	1.0%	5.0%	3.0%	3.0%	2.0%	1.5%	5.0%	1.5%
HY and NR names	2.0%	4.0%	12.0%	7.0%	8.5%	5.5%	5.0%	12.0%	5.0%

(4)

For buckets 1 to 7, the correlation parameter ρ_kl between two weighted sensitivities WS_k and WS_i is calculated as follows, where:

ρ_tenor is equal to 100% if the two tenors are the same and 90% otherwise;

ρ_name is equal to 100% if the two names are the same, 90% if the two names are distinct, but legally related and 50% otherwise;

ρ_quality is equal to 100% if the credit quality of the two names is the same (i.e. IG and IG or HY/NR and HY/NR) and 80% otherwise.

ρ_kl = ρ_tenor ∙ ρ_name ∙ ρ_quality

(5)

For bucket 8, the correlation parameter ρ_kl between two weighted sensitivities WS_k and WS_i is calculated as follows, where

ρ_tenor is equal to 100% if the two tenors are the same and 90% otherwise;

ρ_name is equal to 100% if the two indices are the same and of the same series, 90% if the two indices are the same, but of distinct series, and 80% otherwise;

ρ_quality is equal to 100% if the credit quality of the two indices is the same (ie IG and IG or HY and HY) and 80% otherwise.

ρ_kl = ρ_tenor ∙ ρ_name ∙ ρ_quality

Reference credit spread buckets, risk factors, sensitivities, risk weights and correlations

11.66.

Reference credit spread risk is subject to both delta and vega risk capital requirements. Buckets for delta and vega risks are set as follows, where IG, HY and NR represent “investment grade”, “high yield” and “not rated” as specified for the BA-CVA in 11.16 of this framework:

Table 8: Buckets for reference credit spread risk
Bucket number	Credit quality	Sector
1	IG	Sovereigns including central banks, multilateral development banks
2		Local government, government-backed non-financials, education and public administration
3		Financials including government-backed financials
4		Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying
5		Consumer goods and services, transportation and storage, administrative and support service activities
6		Technology, telecommunications
7		Health care, utilities, professional and technical activities
8	(HY) and NR	Sovereigns including central banks, multilateral development banks
9		Local government, government-backed non-financials, education and public administration
10		Financials including government-backed financials
11		Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying
12		Consumer goods and services, transportation and storage, administrative and support service activities
13		Technology, telecommunications
14		Health care, utilities, professional and technical activities
15	(Not applicable)	Other sector
16	IG	Qualified Indices
17	HY	Qualified Indices

11.67.

For reference credit spread delta and Vega risks, cross-bucket correlations γ_bc are set as follows:

(1)

The cross-bucket correlations γ_bc between buckets of the same credit quality (ie either IG or HY/NR) are set as follows:

Table 9: Cross-bucket correlations for reference credit spread risk
Bucket	1/8	2/9	3/10	4/11	5/12	6/13	7/14	15	16	17
1/8	100%	75%	10%	20%	25%	20%	15%	0%	45%	45%
2/9		100%	5%	15%	20%	15%	10%	0%	45%	45%
3/10			100%	5%	15%	20%	5%	0%	45%	45%
4/11				100%	20%	25%	5%	0%	45%	45%
5/12					100%	25%	5%	0%	45%	45%
6/13						100%	5%	0%	45%	45%
7/14							100%	0%	45%	45%
15								100%	0%	0%
16									100%	75%
17										100%

(2)

For cross-bucket correlations γ_bc between buckets 1 to 14 of different credit quality (i.e. IG and HY/NR), the correlations γ_bc specified in 11.67 of this framework (1) are divided by 2.

11.68.

Reference credit spread delta risk factors for a given bucket:

(1)

The single reference credit spread delta risk factor is a simultaneous absolute shift of the credit spreads of all tenors for all reference names in the bucket.

(2)

The sensitivity to reference credit spread delta risk is measured by simultaneously shifting the credit spreads of all tenors for all reference names in the bucket by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.

(3)

The risk weights RW_k are set as follows depending on the reference name's bucket:

Table 10: Risk weights for reference credit spread delta risk
IG bucket	1	2	3	4	5	6	7	8	9
Risk weigh	0.5%	1.0%	5.0%	3.0%	3.0%	2.0%	1.5%	2.0%	4.0%
HY/NR bucket	10	11	12	13	14	15	16	17
Risk weight	12.0%	7.0%	8.5%	5.5%	5.0%	12.0%	1.5%	5.0%

11.69.

Reference credit spread vega risk factors for a given bucket:

(1)

The single reference credit spread Vega risk factor is a simultaneous relative shift of the volatilities of credit spreads of all tenors for all reference names in the bucket.

(2)

The sensitivity to the reference credit spread vega risk factor is measured by simultaneously shifting the volatilities of credit spreads of all tenors for all reference names in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.

(3)

Risk weights for reference credit spread volatilities ??_? are set to 100%.

Equity buckets, risk factors, sensitivities, risk weights and correlations

11.70.

For equity delta and vega risks, buckets are set as follow, where:

(1)

Market capitalization (“market cap”) is defined as the sum of the market capitalizations of the same legal entity or group of legal entities across all stock markets globally. The reference to “group of legal entities” covers cases where the listed entity is a parent company of a group of legal entities. Under no circumstances should the sum of the market capitalizations of multiple related listed entities be used to determine whether a listed entity is “large market cap” or “small market cap”.

(2)

“Large market cap” is defined as a market capitalization equal to or greater than USD 2 billion and “small market cap” is defined as a market capitalization of less than USD 2 billion.

(3)

The advanced economies are Canada, the United States, Mexico, the euro area, the non-euro area western European countries (the United Kingdom, Norway, Sweden, Denmark and Switzerland), Japan, Oceania (Australia and New Zealand), Singapore and Hong Kong SAR.

(4)

To assign a risk exposure to a sector, banks must rely on a classification that is commonly used in the market for grouping issuers by industry sector. The bank must assign each issuer to one of the sector buckets in the table above and it must assign all issuers from the same industry to the same sector. Risk positions from any issuer that a bank cannot assign to a sector in this fashion must be assigned to the “other sector” (i.e. bucket 11). For multinational multi-sector equity issuers, the allocation to a particular bucket must be done according to the most material region and sector in which the issuer operates.

Table 11: Buckets for equity risk
Bucket number	Size	Region	Sector
1	Large	Emerging market economies	Consumer goods and services, transportation and storage, administrative and support service activities, healthcare, utilities
2			Telecommunications, industrials
3			Basic materials, energy, agriculture, manufacturing, mining and quarrying
4			Financials including government-backed financials, real estate activities, technology
5		Advanced economies	Consumer goods and services, transportation and storage, administrative and support service activities, healthcare, utilities
6			Telecommunications, industrials
7			Basic materials, energy, agriculture, manufacturing, mining and quarrying
8			Financials including government-backed financials, real estate activities, technology
9	Small	Emerging market economies	All sectors described under bucket numbers 1, 2, 3, and 4
10	Small	Advanced economies	All sectors described under bucket numbers 5, 6, 7, and 8
11	(Not applicable)		Other sector
12	Large cap, advanced economies		Qualified Indices
13	Other		Qualified Indices

11.71.

For equity delta and vega risks, cross-bucket correlation γ_bc is set at 15% for all cross-bucket pairs that fall within bucket numbers 1 to 10. The cross-bucket correlation between buckets 12 and 13 is set at 75% and the cross bucket correlation between buckets 12 or 13 and any of the buckets 1-10 is 45%. γ_bc is set at 0% for all cross-bucket pairs that include bucket 11.

11.72.

Equity delta risk factors for a given bucket:

(1)

The single equity delta risk factor is a simultaneous relative shift of equity spot prices for all reference names in the bucket.

(2)

The sensitivity to the equity delta risk factors is measured by simultaneously shifting the equity spot prices for all reference names in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.

(3)

Risk weights RW_k are set as follows depending on the reference name's bucket:

Table 12: Risk weights for equity delta risk
Bucket number	Risk weight
1	55%
2	60%
3	45%
4	55%
5	30%
6	35%
7	40%
8	50%
9	70%
10	50%
11	70%
12	15%
13	25%

11.73.

Equity Vega risk factors for a given bucket:

(1)

The single equity vega risk factor is a simultaneous relative shift of the volatilities for all reference names in the bucket.

(2)

The sensitivity to equity vega risk factors are measured by simultaneously shifting the volatilities for all reference names in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.

(3)

The risk weights for equity volatilities RW_k are set to 78% for large market capitalization buckets and to 100% for other buckets.

Commodity buckets, risk factors, sensitivities, risk weights and correlations

11.74.

For commodity delta and vega risks, buckets are set as follows:

Table 13: Buckets for commodity risk
Bucket number	Commodity group	Examples
1	Energy – Solid combustibles	coal, charcoal, wood pellets, nuclear fuel (such as uranium)
2	Energy – Liquid combustibles	crude oil (such as Light-sweet, heavy, WTI and Brent); biofuels (such as bioethanol and biodiesel); petrochemicals (such as propane, ethane, gasoline, methanol and butane); refined fuels (such as jet fuel, kerosene, gasoil, fuel oil, naptha, heating oil and diesel)
3	Energy – Electricity and carbon trading	electricity (such as spot, day-ahead, peak and off-peak); carbon emissions trading (such as certified emissions reductions, in delivery month EUA, RGGI CO2 allowance and renewable energy certificates)
4	Freight	dry-bulk route (such as capesize, panamex, handysize and supramax); liquid-bulk/gas shipping route (such as suezmax, aframax and very large crude carriers)
5	Metals – nonprecious	base metal (such as aluminum, copper, lead, nickel, tin and zinc); steel raw materials (such as steel billet, steel wire, steel coil, steel scrap and steel rebar, iron ore, tungsten, vanadium, titanium and tantalum); minor metals (such as cobalt, manganese, molybdenum)
6	Gaseous combustibles	natural gas; liquefied natural gas
7	Precious metals (including gold)	gold; silver; platinum; palladium
8	Grains & oilseed	corn; wheat; soybean (such as soybean seed, soybean oil and soybean meal); oats; palm oil; canola; barley; rapeseed (such as rapeseed seed, rapeseed oil, and rapeseed meal); red bean, sorghum; coconut oil; olive oil; peanut oil; sunflower oil; rice
9	Livestock & dairy	cattle (such live and feeder); poultry; lamb; fish; shrimp; dairy (such as milk, whey, eggs, butter and cheese)
10	Softs and other agriculturals	cocoa; coffee (such as arabica and robusta); tea; citrus and orange juice; potatoes; sugar; cotton; wool; lumber and pulp; rubber
11	Other commodity	industrial minerals (such as potash, fertilizer and phosphate rocks), rare earths; terephthalic acid; flat glass

11.75.

For commodity delta and vega risks, cross-bucket correlation γ_bc is set at 20% for all cross-bucket pairs that fall within bucket numbers 1 to 10. γ_bc is set at 0% for all cross-bucket pairs that include bucket 11.

11.76.

Commodity delta risk factors for a given bucket:

(1)

The single commodity delta risk factor is a simultaneous relative shift of commodity spot prices for all commodities in the bucket.

(2)

The sensitivities to commodity delta risk factors are measured by shifting the spot prices of all commodities in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.

(3)

The risk weights RW_k are set as follows depending on the reference name's bucket:

Table 14: Risk weights for commodity delta risk
Bucket	1	2	3	4	5	6	7	8	9	10	11
RW	30%	35%	60%	80%	40%	45%	20%	35%	25%	35%	50%

11.77.

Commodity vega risk factors for a given bucket:

(1)

The single commodity vega risk factor is a simultaneous relative shift of the volatilities for all commodities in the bucket.

(2)

The sensitivity to commodity vega risk factors is measured by simultaneously shifting the volatilities for all commodities in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.

(3)

Risk weights for commodity volatilities RW_k are set to 100%.

⁴⁴ Note that the formula in 11.52 is set out under the convention that the CVA is positive as specified in 11.32 (1). It intends to recognize the risk reducing effect of hedging. For example, when hedging the counterparty credit spread component of CVA risk for a specific counterparty by buying credit protection on the counterparty: if the counterparty’s credit spread widens, the CVA (expressed as a positive value) increases resulting in the positive CVA sensitivity to the counterparty credit spread. At the same time, as the value of the hedge from the bank’s perspective increases as well (as credit protection becomes more valuable), the sensitivity of the hedge is also positive. The positive weighted sensitivities of the CVA and its hedge offset each other using the formula with the minus sign. If CVA loss had been expressed as a negative value, the minus sign in 11.52 would have been replaced by a plus sign.
⁴⁵ For example, if a SAR-reporting bank holds an instrument that references the USD-GBP exchange rate, the bank must measure CVA sensitivity both to the SAR-GBP exchange rate and to the SAR- USD exchange rate.