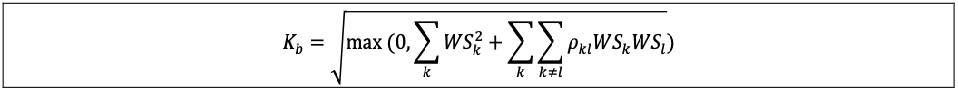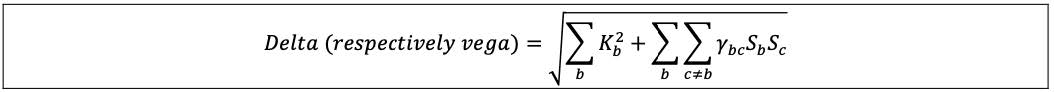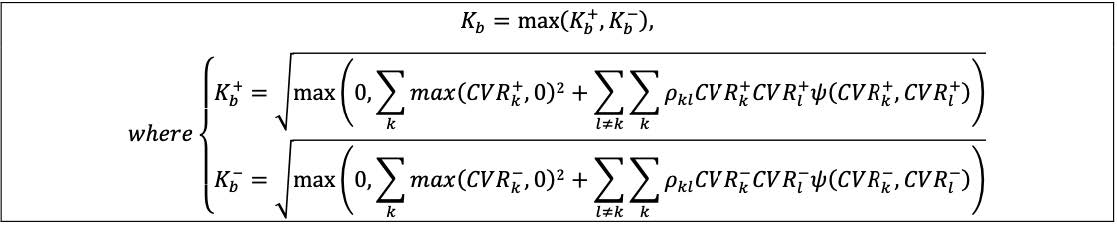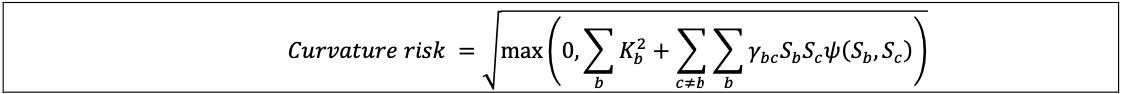| 7.3 | As set out in [7.1], the capital requirement under the sensitivities-based method is calculated by aggregating delta, vega and curvature capital requirements. The relevant paragraphs that describe this process are as follows:
| | |
| | (1) | The risk factors for delta, vega and curvature risks for each risk class are defined in [7.8] to [7.14].
| |
| | (2) | The methods to risk weight sensitivities to risk factors and aggregate them to calculate delta and vega risk positions for each risk class are set out in [7.4] and [7.15] to [7.95], which include the definition of delta and vega sensitivities, definition of buckets, risk weights to apply to risk factors, and correlation parameters.
| |
| | (3) | The methods to calculate curvature risk are set out in [7.5] and [7.96] to [7.101], which include the definition of buckets, risk weights and correlation parameters.
| |
| | (4) | The risk class level capital requirement calculated above must be aggregated to obtain the capital requirement at the entire portfolio level as set out in [7.6] and [7.7].
| |
Calculation of the delta and vega risk capital requirement for each risk class
| | |
| 7.4 | For each risk class, a bank must determine its instruments’ sensitivity to a set of prescribed risk factors, risk weight those sensitivities, and aggregate the resulting risk-weighted sensitivities separately for delta and vega risk using the following step-by-step approach:
| | |
| | (1) | For each risk factor (as defined in [7.8] to [7.14]), a sensitivity is determined as set out in [7.15] to [7.38].
| |
| | (2) | Sensitivities to the same risk factor must be netted to give a net sensitivity Sk across all instruments in the portfolio to each risk factor k. In calculating the net sensitivity, all sensitivities to the same given risk factor (eg all sensitivities to the one-year tenor point of the three-month Euribor swap curve) from instruments of opposite direction should offset, irrespective of the instrument from which they derive. For instance, if a bank’s portfolio is made of two interest rate swaps on three-month Euribor with the same fixed rate and same notional but of opposite direction, the GIRR on that portfolio would be zero.
| |
| | (3) | The weighted sensitivity WSk is the product of the net sensitivity Sk and the corresponding risk weight RWk as defined in [7.39] to [7.95].
| |
|
| | (4) | Within bucket aggregation: the risk position for delta (respectively vega) bucket b, Kb, must be determined by aggregating the weighted sensitivities to risk factors within the same bucket using the prescribed correlation ρkɭ set out in the following formula, where the quantity within the square root function is floored at zero:
| |
|
| | (5) | Across bucket aggregation: The delta (respectively vega) risk capital requirement is calculated by aggregating the risk positions across the delta (respectively vega) buckets within each risk class, using the corresponding prescribed correlations γbc as set out in the following formula, where:
| |
| | | (a) | Sb = ∑k WSk for all risk factors in bucket b, and Sc = ∑k WSk in bucket c.
|
| | | (b) | If these values for Sb and Sc described in above [7.4](5)(a) produce a negative number for the overall sum of ∑b Kb2 + ∑b ∑c≠b γbc SbSc, the bank is to calculate the delta (respectively vega) risk capital requirement using an alternative specification whereby:
|
| | | | (i) | Sb=max [min (∑k WSk, Kb), - Kb] for all risk factors in bucket b; and
| | |
| | | | (ii) | Sc=max [min (∑k WSk, Kc), - Kc] for all risk factors in bucket c.
| | |
|
Calculation of the curvature risk capital requirement for each risk class
| | |
| 7.5 | For each risk class, to calculate curvature risk capital requirements a bank must apply an upward shock and a downward shock to each prescribed risk factor and calculate the incremental loss for instruments sensitive to that risk factor above that already captured by the delta risk capital requirement using the following step- by-step approach:
| | |
| | (1) | For each instrument sensitive to curvature risk factor k, an upward shock and a downward shock must be applied to k. The size of shock (ie risk weight) is set out in [7.98] and [7.99].
| |
| | | (a) | For example for GIRR, all tenors of all the risk free interest rate curves within a given currency (eg three-month Euribor, six-month Euribor, one year Euribor, etc for the euro) must be shifted upward applying the risk weight as set out in [7.99]. The resulting potential loss for each instrument, after the deduction of the delta risk positions, is the outcome of the upward scenario. The same approach must be followed on a downward scenario.
|
| | | (b) | If the price of an instrument depends on several risk factors, the curvature risk must be determined separately for each risk factor.
|
| | (2) | The net curvature risk capital requirement, determined by the values CVR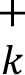 and CVR and CVR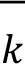 for a bank’s portfolio for risk factor k described in above [7.5] (1) is calculated by the formula below. It calculates the aggregate incremental loss beyond the delta capital requirement for the prescribed shocks, where for a bank’s portfolio for risk factor k described in above [7.5] (1) is calculated by the formula below. It calculates the aggregate incremental loss beyond the delta capital requirement for the prescribed shocks, where
| |
| | | (a) | i is an instrument subject to curvature risks associated with risk factor k;
|
| | | (b) | xk is the current level of risk factor k;
|
| | | (c) | Vi (Xk) is the price of instrument i at the current level of risk factor k;
|
| | | (d) | Vi (Xk(RW (curvature)+)) and Vi (Xk(RW (curvature)-)) denote the price of instrument i after xk is shifted (ie “shocked”) upward and downward respectively;
|
| | | (e) | (curvature) is the risk weight for curvature risk factor k for instrument i; and
|
| | | (f) | Sik is the delta sensitivity of instrument i with respect to the delta risk factor that corresponds to curvature risk factor k, where:
|
| | | | (i) | For the FX and equity risk classes, Sik is the delta sensitivity of instrument i; and
| | |
| | | | (iii) | For the GIRR, CSR and commodity risk classes, Sik is the sum of delta sensitivities to all tenors of the relevant curve of instrument i with respect to curvature risk factor k.
| | |
|
| | (3) | Within bucket aggregation: the curvature risk exposure must be aggregated within each bucket using the corresponding prescribed correlation ρkɭ as set out in the following formula, where:
| |
| | | (a) | The bucket level capital requirement (Kb) is determined as the greater of the capital requirement under the upward scenario ( 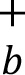 ) and the capital requirement under the downward scenario (Kb ) and the capital requirement under the downward scenario (Kb ). Notably, the selection of upward and downward scenarios is not necessarily the same across the high, medium and low correlations scenarios specified in [7.6]. ). Notably, the selection of upward and downward scenarios is not necessarily the same across the high, medium and low correlations scenarios specified in [7.6].
|
| | | | (i) | Where Kb = K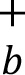 , this shall be termed “selecting the upward scenario”. , this shall be termed “selecting the upward scenario”.
| | |
| | | | (ii) | Where Kb = Kb , this shall be termed “selecting the downward scenario”. , this shall be termed “selecting the downward scenario”.
| | |
| | | | (iii) | In the specific case where K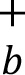 = Kb = Kb if ∑kCVR if ∑kCVR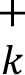 >∑k CVR >∑k CVR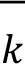 , it is deemed that the upward scenario is selected; otherwise the downward scenario is selected. , it is deemed that the upward scenario is selected; otherwise the downward scenario is selected.
| | |
| | | (b) | Ψ(CVRk, CVRɭ) takes the value 0 if CVRk and CVRɭ both have negative signs and the value 1 otherwise.
|
|
| | (4) | Across bucket aggregation: curvature risk positions must then be aggregated across buckets within each risk class, using the corresponding prescribed correlations γbc, where:
| |
| | | (a) | Sb = ∑k CVR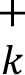 for all risk factors in bucket b, when the upward scenario has been selected for bucket b in above (3)(a). Sb = ∑k CVR for all risk factors in bucket b, when the upward scenario has been selected for bucket b in above (3)(a). Sb = ∑k CVR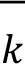 otherwise; and otherwise; and
|
| | | (b) | (Sb, Sc) takes the value 0 if Sb and Sc both have negative signs and 1 otherwise.
|
|
The delta used for the calculation of the curvature risk capital requirement should be the same as that used for calculating the delta risk capital requirement. The assumptions that are used for the calculation of the delta (ie sticky delta for normal or log-normal volatilities) should also be used for calculating the shifted or shocked price of the instrument.
| | |
[7.17] states that banks must determine each delta sensitivity, vega sensitivity and curvature scenario based on instrument prices or pricing models that an independent risk control unit within a bank uses to report market risks or actual profits and losses to senior management. Banks should use zero rate or market rate sensitivities consistent with the pricing models referenced in that paragraph.
| | |
Calculation of aggregate sensitivities-based method capital requirement
| | |
| 7.6 | In order to address the risk that correlations increase or decrease in periods of financial stress, the aggregation of bucket level capital requirements and risk class level capital requirements per each risk class for delta, vega, and curvature risks as specified in [7.4] to [7.5] must be repeated, corresponding to three different scenarios on the specified values for the correlation parameter ρkɭ (correlation between risk factors within a bucket) and γbc (correlation across buckets within a risk class).
| | |
| | (1) | Under the “medium correlations” scenario, the correlation parameters ρkɭ and γbc as specified in [7.39] to [7.101] apply.
| |
| | (2) | Under the “high correlations” scenario, the correlation parameters ρkɭ and γbc that are specified in [7.39] to [7.101] are uniformly multiplied by 1.25, with ρkɭ and γbc subject to a cap at 100%.
| |
| | (3) | Under the “low correlations” scenario, the correlation parameters ρkɭ and γbc that are specified in 7.39 to 7.101] are replaced by ρ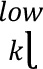 = max(2 x ρkɭ - 100%;75%x ρkɭ) γ = max(2 x ρkɭ - 100%;75%x ρkɭ) γ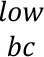 and =max(2x γbc -100%;75%x γbc). and =max(2x γbc -100%;75%x γbc).
| |
| 7.7 | The total capital requirement under the sensitivities-based method is aggregated as follows:
| | |
| | (1) | For each of three correlation scenarios, the bank must simply sum up the separately calculated delta, vega and curvature capital requirements for all risk classes to determine the overall capital requirement for that scenario.
| |
| | (2) | The sensitivities-based method capital requirement is the largest capital requirement from the three scenarios.
| |
| | | (a) | For the calculation of capital requirements for all instruments in all trading desks using the standardised approach as set out in [3.10] (1) and [17.2] and [13.40], the capital requirement is calculated for all instruments in all trading desks.
|
| | | (b) | For the calculation of capital requirements for each trading desk using the standardised approach as if that desk were a standalone regulatory portfolio as set out in [3.8](2), the capital requirements under each correlation scenario are calculated and compared at each trading desk level, and the maximum for each trading desk is taken as the capital requirement.
|