Book traversal links for Sensitivities-Based Method: Definition of Delta Risk Buckets, Risk Weights and Correlations
Sensitivities-Based Method: Definition of Delta Risk Buckets, Risk Weights and Correlations
| No: 44047144 | Date(g): 27/12/2022 | Date(h): 4/6/1444 | Status: In-Force |
| 7.39 | [7.41] to [7.89] set out buckets, risk weights and correlation parameters for each risk class to calculate delta risk capital requirement as set out in [7.4]. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.40 | The prescribed risk weights and correlations in [7.41] to [7.89] have been calibrated to the liquidity adjusted time horizon related to each risk class. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Delta GIRR buckets, risk weights and correlations | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.41 | Each currency is a separate delta GIRR bucket, so all risk factors in risk-free yield curves for the same currency in which interest rate-sensitive instruments are denominated are grouped into the same bucket. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.42 | For calculating weighted sensitivities, the risk weights for each tenor in risk-free yield curves are set in Table 1 as follows: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.43 | The risk weight for the inflation risk factor and the cross-currency basis risk factors, respectively, is set at 1.6%. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.44 | For specified currencies by the Basel Committee,22 the above risk weights may, at the discretion of the bank, be divided by the square root of 2. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.45 | For aggregating GIRR risk positions within a bucket, the correlation parameter ρkl between weighted sensitivities WSk and WSl within the same bucket (ie same currency), same assigned tenor, but different curves is set at 99.90%. In aggregating delta risk positions for cross-currency basis risk for onshore and offshore curves, which must be considered two different curves as set out in [7.8], a bank may choose to aggregate all cross-currency basis risk for a currency (ie “Curr/USD” or “Curr/EUR”) for both onshore and offshore curves by a simple sum of weighted sensitivities. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.46 | The delta risk correlation ρkl between weighted sensitivities WSk and WSl within the same bucket with different tenor and same curve is set in the following Table 2:23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.47 | Between two weighted sensitivities WSk and WSl within the same bucket with different tenor and different curves, the correlation ρkl is equal to the correlation parameter specified in [7.46] multiplied by 99.90%.24 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.48 | The delta risk correlation ρkl between a weighted sensitivity WSk to the inflation curve and a weighted sensitivity WSl to a given tenor of the relevant yield curve is 40%. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.49 | The delta risk correlation ρkl between a weighted sensitivity WSk to a cross-currency basis curve and a weighted sensitivity WSl to each of the following curves is 0%: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | a given tenor of the relevant yield curve; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | the inflation curve; or | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (3) | another cross-currency basis curve (if relevant). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.50 | For aggregating GIRR risk positions across different buckets (ie different currencies), the parameter γbc is set at 50%. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Delta CSR non-securitisations buckets, risk weights and correlations | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.51 | For delta CSR non-securitisations, buckets are set along two dimensions – credit quality and sector – as set out in Table 3. The CSR non-securitisation sensitivities or risk exposures should first be assigned to a bucket defined before calculating weighted sensitivities by applying a risk weight. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Consistent with the treatment of external ratings under SAMA Minimum Capital Requirements for Credit Risk paragraphs 8.10 and 8.12, if there are two ratings which map into different risk weights, the higher risk weight should be applied. If there are three or more ratings with different risk weights, the ratings corresponding to the two lowest risk weights should be referred to and the higher of those two risk weights will be applied. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Consistent with the treatment where there are no external ratings, banks may, subject to SAMA approval: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | For the purpose of assigning delta CSR non-securitisation risk weights, map the internal rating to an external rating, and assign a risk weight corresponding to either “investment grade” or “high yield” in [7.51]; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | For the purpose of assigning default risk weights under the DRC requirement, map the internal rating to an external rating, and assign a risk weight corresponding to one of the seven external ratings in the table included [8.24]; or | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | Apply the risk weights specified in [7.51] and [8.24] for unrated/non-rated categories. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.52 | To assign a risk exposure to a sector, banks must rely on a classification that is commonly used in the market for grouping issuers by industry sector. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | The bank must assign each issuer to one and only one of the sector buckets in the table under [7.51]. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | Risk positions from any issuer that a bank cannot assign to a sector in this fashion must be assigned to the other sector (ie bucket 16). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.53 | For calculating weighted sensitivities, the risk weights for buckets 1 to 18 are set out in Table 4. Risk weights are the same for all tenors (ie 0.5 years, 1 year, 3 years, 5 years, 10 years) within each bucket: Risk weights for buckets for delta CSR non-securitisations | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.54 | For buckets 1 to 15, for aggregating delta CSR non-securitisations risk positions within a bucket, the correlation parameter ρkl between two weighted sensitivities WSk and WSɭ within the same bucket, is set as follows, where: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | ρkl (name) is equal to 1 where the two names of sensitivities k and ∫ are identical, and 35% otherwise; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | ρkl (tenor) is equal to 1 if the two tenors of the sensitivities k and ∫ are identical, and to 65% otherwise; and | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (3) | ρkl (basis) is equal to 1 if the two sensitivities are related to same curves, and 99.90% otherwise. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Bond and CDS credit spreads are considered distinct risk factors under [7.9](1), and ρkl(basis) referenced in [7.54] and [7.55] is meant to capture only the bond-CDS basis. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.55 | For buckets 17 and 18, for aggregating delta CSR non-securitisations risk positions within a bucket, the correlation parameter ρkl between two weighted sensitivities WSk and WSi within the same bucket is set as follows, where: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | ρk (name) is equal to 1 where the two names of sensitivities k and ∫ are identical, and 80% otherwise; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | ρk (tenor) is equal to 1 if the two tenors of the sensitivities k and ∫ are identical, and to 65% otherwise; and | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (3) | ρkl (basis) is equal to 1 if the two sensitivities are related to same curves, and 99.90%. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.56 | The correlations above do not apply to the other sector bucket (ie bucket 16). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | The aggregation of delta CSR non-securitisation risk positions within the other sector bucket (ie bucket 16) would be equal to the simple sum of the absolute values of the net weighted sensitivities allocated to this bucket. The same method applies to the aggregation of vega risk positions. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
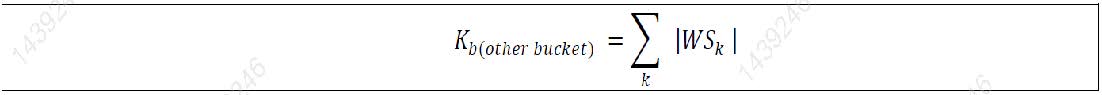 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | The aggregation of curvature CSR non-securitisation risk positions within the other sector bucket (ie bucket 16) would be calculated by the formula below. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
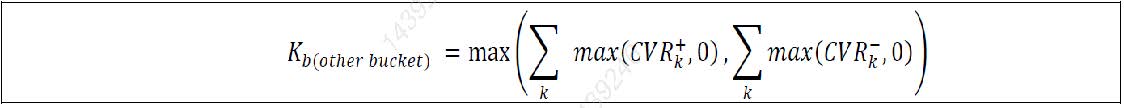 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.57 | For aggregating delta CSR non-securitisation risk positions across buckets 1 to 16, the correlation parameter γbc is set as follows, where: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | γbc(rating) is equal to 50% where the two buckets b and c are both in buckets 1 to 15 and have a different rating category (either IG or HY/NR). γbc(rating) is equal to 1 otherwise; and | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | γbc(sector) is equal to 1 if the two buckets belong to the same sector, and to the specified numbers in Table 5 otherwise. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Delta CSR securitisation (CTP) buckets, risk weights and correlations | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.58 | Sensitivities to CSR arising from the CTP and its hedges are treated as a separate risk class as set out in 7.1]. The buckets, risk weights and correlations for the CSR securitisations (CTP) apply as follows: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | The same bucket structure and correlation structure apply to the CSR securitisations (CTP) as those for the CSR non-securitisation framework as set out in [7.51] to [7.57] with an exception of index buckets (ie buckets 17 and 18). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | The risk weights and correlation parameters of the delta CSR nonsecuritisations are modified to reflect longer liquidity horizons and larger basis risk as specified in [7.59] to [7.61]. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.59 | For calculating weighted sensitivities, the risk weights for buckets 1 to 16 are set out in Table 6. Risk weights are the same for all tenors (ie 0.5 years, 1 year, 3 years, 5 years, 10 years) within each bucket: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.60 | For aggregating delta CSR securitisations (CTP) risk positions within a bucket, the delta risk correlation ρkl is derived the same way as in [7.54] and [7.55], except that the correlation parameter applying when the sensitivities are not related to same curves, ρkl (basis), is modified. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | ρkl (basis) is now equal to 1 if the two sensitivities are related to same curves, and 99.00% otherwise. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | The identical correlation parameters for ρkl(name) and ρkl(tenor) to CSR non-securitisation as set out in [7.54] and [7.55] apply. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.61 | For aggregating delta CSR securitisations (CTP) risk positions across buckets, the correlation parameters for γbc are identical to CSR non-securitisation as set out in [7.57]. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Delta CSR securitisation (non-CTP) buckets, risk weights and correlations | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.62 | For delta CSR securitisations not in the CTP, buckets are set along two dimensions– credit quality and sector – as set out in Table 7. The delta CSR securitisation (non-CTP) sensitivities or risk exposures must first be assigned to a bucket before calculating weighted sensitivities by applying a risk weight. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.63 | To assign a risk exposure to a sector, banks must rely on a classification that is commonly used in the market for grouping tranches by type. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | The bank must assign each tranche to one of the sector buckets in above Table 7. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | Risk positions from any tranche that a bank cannot assign to a sector in this fashion must be assigned to the other sector (ie bucket 25). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.64 | For calculating weighted sensitivities, the risk weights for buckets 1 to 8 (senior IG) are set out in Table 8: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.65 | The risk weights for buckets 9 to 16 (non-senior investment grade) are then equal to the corresponding risk weights for buckets 1 to 8 scaled up by a multiplication by 1.25. For instance, the risk weight for bucket 9 is equal to 1.25 × 0.9% = 1.125%. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.66 | The risk weights for buckets 17 to 24 (high yield and non-rated) are then equal to the corresponding risk weights for buckets 1 to 8 scaled up by a multiplication by 1.75. For instance, the risk weight for bucket 17 is equal to 1.75 × 0.9% = 1.575%. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.67 | The risk weight for bucket 25 is set at 3.5%. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.68 | For aggregating delta CSR securitisations (non-CTP) risk positions within a bucket, the correlation parameter ρkl between two sensitivities WSk and WSl within the same bucket, is set as follows, where: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | ρkl (tranche) is equal to 1 where the two names of sensitivities k and l are within the same bucket and related to the same securitisation tranche (more than 80% overlap in notional terms), and 40% otherwise; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | ρkl (tenor) is equal to 1 if the two tenors of the sensitivities k and l are identical, and to 80% otherwise; and | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (3) | ρkl (basis) is equal to 1 if the two sensitivities are related to same curves, and 99.90% otherwise. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [7.68] includes ρkl (tranche) , which equals 1 where the two sensitivities within the same bucket are related to the same securitisation tranche, or 40% otherwise. There is no issuer factor. This mean a two sensitivities relating to the same issuer but different tranches require 40% correlation. There is no granularity for issuers in the delta CSR securitisation part as set out in [7.10]. Where two tranches have exactly the same issuer, same tenor and same basis, but different tranches (ie different credit quality), the correlation must be 40%. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.69 | The correlations above do not apply to the other sector bucket (ie bucket 25). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | The aggregation of delta CSR securitisations (non-CTP) risk positions within the other sector bucket would be equal to the simple sum of the absolute values of the net weighted sensitivities allocated to this bucket. The same method applies to the aggregation of vega risk position. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | The aggregation of curvature CSR risk positions within the other sector bucket (ie bucket 16) would be calculated by the formula below. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
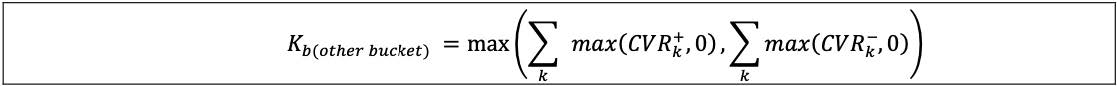 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.70 | For aggregating delta CSR securitisations (non-CTP) risk positions across buckets 1 to 24, the correlation parameter γbc is set as 0%. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.71 | For aggregating delta CSR securitisations (non-CTP) risk positions between the other sector bucket (ie bucket 25) and buckets 1 to 24, the correlation parameter γbc is set at 1. Bucket level capital requirements will be simply summed up to the overall risk class level capital requirements, with no diversification or hedging effects recognised with any bucket. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Equity risk buckets, risk weights and correlations | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.72 | For delta equity risk, buckets are set along three dimensions – market capitalisation, economy and sector – as set out in Table 9. The equity risk sensitivities or exposures must first be assigned to a bucket before calculating weighted sensitivities by applying a risk weight. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.73 | Market capitalisation (market cap) is defined as the sum of the market capitalisations based on the market value of the total outstanding shares issued by the same listed legal entity or a group of legal entities across all stock markets globally, where the total outstanding shares issued by the group of legal entities refer to cases where the listed entity is a parent company of a group of legal entities. Under no circumstances should the sum of the market capitalisations of multiple related listed entities be used to determine whether a listed entity is “large market cap” or “small market cap”. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.74 | Large market cap is defined as a market capitalisation equal to or greater than USD 2 billion and small market cap is defined as a market capitalisation of less than USD 2 billion. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.75 | The advanced economies are Canada, the United States, Mexico, the euro area, the non-euro area western European countries (the United Kingdom, Norway, Sweden, Denmark and Switzerland), Japan, Oceania (Australia and New Zealand), Singapore and Hong Kong SAR. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| An equity issuer must be allocated to a particular bucket according to the most material country or region in which the issuer operates. As stated in [7.76]: “For multinational multisector equity issuers, the allocation to a particular bucket must be done according to the most material region and sector in which the issuer operates. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.76 | To assign a risk exposure to a sector, banks must rely on a classification that is commonly used in the market for grouping issuers by industry sector. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | The bank must assign each issuer to one of the sector buckets in the table under [7.72] and it must assign all issuers from the same industry to the same sector. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | Risk positions from any issuer that a bank cannot assign to a sector in this fashion must be assigned to the other sector (ie bucket 11). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (3) | For multinational multi-sector equity issuers, the allocation to a particular bucket must be done according to the most material region and sector in which the issuer operates. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.77 | For calculating weighted sensitivities, the risk weights for the sensitivities to each of equity spot price and equity repo rates for buckets 1 to 13 are set out in Table 10: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.78 | For aggregating delta equity risk positions within a bucket, the correlation parameter ρkl between two sensitivities WSk and WSl within the same bucket is set at as follows | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | The correlation parameter ρkl is set at 99.90%, where: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (a) | one is a sensitivity to an equity spot price and the other a sensitivity to an equity repo rates; and | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (b) | both are related to the same equity issuer name. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | The correlation parameter ρkl is set out in (a) to (d) below, where both sensitivities are to equity spot price, and where: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (a) | 15% between two sensitivities within the same bucket that fall under large market cap, emerging market economy (bucket number 1, 2, 3 or 4). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (b) | 25% between two sensitivities within the same bucket that fall under large market cap, advanced economy (bucket number 5, 6, 7 or 8). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (c) | 7.5% between two sensitivities within the same bucket that fall under small market cap, emerging market economy (bucket number 9). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (d) | 12.5% between two sensitivities within the same bucket that fall under small market cap, advanced economy (bucket number 10). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (e) | 80% between two sensitivities within the same bucket that fall under either index bucket (bucket number 12 or 13) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (3) | The same correlation parameter ρkl as set out in above (2)(a) to (d) apply, where both sensitivities are to equity repo rates. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (4) | The correlation parameter ρkl is set as each parameter specified in above (2)(a) to (d) multiplied by 99.90%, where: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (a) | One is a sensitivity to an equity spot price and the other a sensitivity to an equity repo rate; and | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (b) | Each sensitivity is related to a different equity issuer name. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.79 | The correlations set out above do not apply to the other sector bucket (ie bucket 11). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | The aggregation of equity risk positions within the other sector bucket capital requirement would be equal to the simple sum of the absolute values of the net weighted sensitivities allocated to this bucket. The same method applies to the aggregation of vega risk positions. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | The aggregation of curvature equity risk positions within the other sector bucket (ie bucket 11) would be calculated by the formula: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
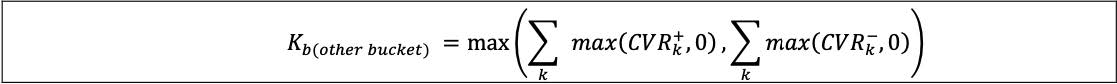 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.80 | For aggregating delta equity risk positions across buckets 1 to 13, the correlation parameter γbc is set at: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | 15% if bucket b and bucket c fall within bucket numbers 1 to 10; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | 0% if either of bucket b and bucket c is bucket 11; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (3) | 75% if bucket b and bucket c are bucket numbers 12 and 13 (i.e. one is bucket 12, one is bucket 13); and | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (4) | 45% otherwise. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Commodity risk buckets, risk weights and correlations | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.81 | For delta commodity risk, 11 buckets that group commodities by common characteristics are set out in Table 11. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.82 | For calculating weighted sensitivities, the risk weights for each bucket are set out in Table 11: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.83 | For the purpose of aggregating commodity risk positions within a bucket using a correlation parameter, the correlation parameter ρkl between two sensitivities WSk and WSl within the same bucket, is set as follows, where: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | ρkl(cty) is equal to 1 where the two commodities of sensitivities k and l are identical, and to the intra-bucket correlations in Table 12 otherwise, where, any two commodities are considered distinct commodities if in the market two contracts are considered distinct when the only difference between each other is the underlying commodity to be delivered. For example, WTI and Brent in bucket 2 (ie energy – liquid combustibles) would typically be treated as distinct commodities; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | ρkl(tenor) is equal to 1 if the two tenors of the sensitivities k and l are identical, and to 99.00% otherwise; and | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (3) | ρkl(basis) is equal to 1 if the two sensitivities are identical in the delivery location of a commodity, and 99.90% otherwise. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Instruments with a spread as their underlying are considered sensitive to different risk factors. In the example cited, the swap will be sensitive to both WTI and Brent, each of which require a capital charge at the risk factor level (ie delta of WTI and delta of Brent). The correlation to aggregate capital charges is specified in [7.83]. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.84 | For determining whether the commodity correlation parameter (ρkl(cty)) as set out in Table 12 in [7.83](1)(a) should apply, this paragraph provides non-exhaustive examples of further definitions of distinct commodities as follows: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | For bucket 3 (energy – electricity and carbon trading): | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (a) | Each time interval (i) at which the electricity can be delivered and (ii) that is specified in a contract that is made on a financial market is considered a distinct electricity commodity (eg peak and off-peak). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (b) | Electricity produced in a specific region (eg Electricity NE, Electricity SE or Electricity North) is considered a distinct electricity commodity. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | For bucket 4 (freight): | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (a) | Each combination of freight type and route is considered a distinct commodity. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (b) | Each week at which a good has to be delivered is considered a distinct commodity. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.85 | For aggregating delta commodity risk positions across buckets, the correlation parameter ybc is set as follows: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1) | 20% if bucket b and bucket c fall within bucket numbers 1 to 10; and | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (2) | 0% if either bucket b or bucket c is bucket number 11. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Foreign exchange risk buckets, risk weights and correlations | ||||
| 7.86 | An FX risk bucket is set for each exchange rate between the currency in which an instrument is denominated and the reporting currency. | |||
| 7.87 | A unique relative risk weight equal to 15% applies to all the FX sensitivities. | |||
| 7.88 | For specified currency pairs,32 and for currency pairs forming first- order crosses across these specified currency pairs,33 the above risk weight may at the discretion of the bank be divided by the square root of 2. | |||
| 7.89 | For aggregating delta FX risk positions across buckets, the correlation parameter Ybc is uniformly set to 60%. | |||
22 Specified currencies by the Basel Committee are: EUR, USD, GBP, AUD, JPY, SEK, CAD as well as the domestic reporting currency of a bank.
23 The delta GIRR correlation parameters (ρkl) set out in Table 2 is determined by ma ![]() , where Tk (respectivelyTl) is the tenor that relates to WSk (respectively WSl); and θ is set at 3%. For example, the correlation between a sensitivity to the one-year tenor of the Eonia swap curve and the a sensitivity to the five-year tenor of the Eonia swap curve in the same currency is max
, where Tk (respectivelyTl) is the tenor that relates to WSk (respectively WSl); and θ is set at 3%. For example, the correlation between a sensitivity to the one-year tenor of the Eonia swap curve and the a sensitivity to the five-year tenor of the Eonia swap curve in the same currency is max 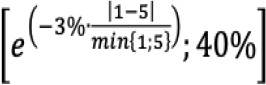 = 88.69%
= 88.69%
24 For example, the correlation between a sensitivity to the one-year tenor of the Eonia swap curve and a sensitivity to the five-year tenor of the three-month Euribor swap curve in the same currency is (88.69%) . (0.999) = 88.60%.
25 Covered bonds must meet the definition provided by Large Exposure Rules for Banks issued via SAMA circular No. 1651 / 67 dated 09/01/1441.
26 Credit quality is not a differentiating consideration for this bucket.
27 For covered bonds that are rated AA- or higher, the applicable risk weight may at the discretion of the bank be 1.5%..
28 For example, a sensitivity to the five-year Apple bond curve and a sensitivity to the 10- year Google CDS curve would be 35% . .65% . 99.90% = 22.73%.
29 Credit quality is not a differentiating consideration for this bucket.
30 Market capitalisation or economy (ie advanced or emerging market) is not a differentiating consideration for this bucket.
31 For example, the correlation between the sensitivity to Brent, one-year tenor, for delivery in Le Havre and the sensitivity to WTI, five-year tenor, for delivery in Oklahoma is 95% - 99.00% - 99.90% = 93.96%.
32 Specified currency pairs are: SAR/USD, USD/EUR, USD/JPY, USD/GBP, USD/AUD, USD/CAD, USD/CHF, USD/MXN, USD/CNY, USD/NZD, USD/RUB, USD/HKD, USD/SGD, USD/TRY, USD/KRW, USD/SEK, USD/ZAR, USD/INR, USD/NOK, USD/BRL.
33 example, EUR/AUD is not among the selected currency pairs specified by the Basel Committee, but is a first-order cross of USD/EUR and USD/AUD.

