Minimum Capital Requirements for Counterparty Credit Risk (CCR) and Credit Valuation Adjustment (CVA)
No: 44047144 Date(g): 27/12/2022 | Date(h): 4/6/1444 Status: In-Force 1. Introduction
The Basel III framework on Counterparty Credit Risk includes a comprehensive, non-modelled approach for measuring counterparty credit risk arising from derivative contracts, Securities Financing transaction (SFT) and cash transactions in securities, foreign exchange and commodities. With the continued growth of the derivative market and banks’ increasing use of financial instruments and structured products for yield enhancement and/or risk management purposes, it is essential for them to have the necessary systems and expertise for managing any CCR associated with those activities.
This Framework covers both Counterparty Default Risk as well as the Credit Valuation Adjustment (CVA) to calculate the risk of losses arising from the changes in the value of the CVA in response to the changes in the counterparty credit spreads and market risk factors that drive prices of derivative transactions and SFTs. Banks that are below the CVA materiality threshold may opt not to calculate its CVA capital requirements. A bank must regularly review and update its materiality assessment to reflect any significant changes in materiality.
This framework is issued by SAMA in exercise of the authority vested in SAMA under the Central Bank Law issued via Royal Decree No. M/36 dated 11/04/1442H, and the Banking Control Law issued 01/01/1386H.
This Framework supersedes any conflicting requirements in previous circulars in this regard (GDBC-371000101120, GDBC-410382700000, and GDBC-361000021954).
2. Scope of Application
2.1. This framework applies to all domestic banks both on a consolidated basis, which include all branches and subsidiaries, and on a standalone basis.
2.2. This framework is not applicable to Foreign Banks Branches operating in the kingdom of Saudi Arabia, and the branches shall comply with the regulatory capital requirements stipulated by their respective home regulators.
3. Definitions
General Terms
Counterparty credit risk (CCR) The risk that the counterparty to a transaction could default before the final settlement of the transaction's cash flows. An economic loss would occur if the transactions or portfolio of transactions with the counterparty has a positive economic value at the time of default. Unlike a firm's exposure to credit risk through a loan, where the exposure to credit risk is unilateral and only the lending bank faces the risk of loss, CCR creates a bilateral risk of loss: the market value of the transaction can be positive or negative to either counterparty to the transaction. The market value is uncertain and can vary over time with the movement of underlying market factors.
A central counterparty (CCP) A clearing house that interposes itself between counterparties to contracts traded in one or more financial markets, becoming the buyer to every seller and the seller to every buyer and thereby ensuring the future performance of open contracts. A CCP becomes counterparty to trades with market participants through novation, an open offer system, or another legally binding arrangement. For the purposes of the capital framework, a CCP is a financial institution.
A qualifying central counterparty (QCCP) An entity that is licensed to operate as a CCP (including a license granted by way of confirming an exemption), and is permitted by the appropriate regulator/overseer Capital Market Authority (CMA) to operate as such with respect to the products offered. This is subject to the provision that the CCP is based and prudentially supervised in a jurisdiction where the relevant regulator/overseer has established. (Saudi Arabia) and publicly indicated that it applies to the CCP on an ongoing basis, domestic rules and regulations that are consistent with the Principles for Financial Market Infrastructures issued by the Committee on Payments and Market Infrastructures and the International Organization of Securities Commissions.
1) Where the CCP is in a jurisdiction that does not have a CCP regulator applying the Principles to the CCP, then SAMA may make the determination of whether the CCP meets this definition.
2) In addition, for a CCP to be considered a QCCP, the requirements of 8.37 must be met to permit each clearing member bank to calculate its capital requirement for its default fund exposures.
A clearing member A member of, or a direct participant in, a CCP that is entitled to enter into a transaction with the CCP, regardless of whether it enters into trades with a CCP for its own hedging, investment or speculative purposes or whether it also enters into trades as a financial intermediary between the CCP and other market participants.
For the purposes of the CCR standard, where a CCP has a link to a second CCP, that second CCP is to be treated as a clearing member of the first CCP. Whether the second CCP's collateral contribution to the first CCP is treated as initial margin or a default fund contribution will depend upon the legal arrangement between the CCPs. SAMA should be consulted to determine the treatment of this initial margin and default fund contributions.
A client is a party to a transaction with a CCP through either a clearing member acting as a financial intermediary, or a clearing member guaranteeing the performance of the client to the CCP.
A multi-level Client structure One in which banks can centrally clear as indirect clients; that is, when clearing services are provided to the bank by an institution which is not a direct clearing member, but is itself a client of a clearing member or another clearing client. For exposures between clients and clients of clients, we use the term higher level client for the institution providing clearing services; and the term lower level client for the institution clearing through that client.
Initial margin A clearing member's or client's funded collateral posted to the CCP to mitigate the potential future exposure (PFE) of the CCP to the clearing member arising from the possible future change in the value of their transactions. For the purposes of the calculation of counterparty credit risk capital requirements, initial margin does not include contributions to a CCP for mutualized loss sharing arrangements (i.e. in case a CCP uses initial margin to mutualize losses among the clearing members, it will be treated as a default fund exposure). Initial margin includes collateral deposited by a clearing member or client in excess of the minimum amount required, provided the CCP or clearing member may, in appropriate cases, prevent the clearing member or client from withdrawing such excess collateral.
Variation margin A clearing member's or client's funded collateral posted on a daily or intraday basis to a CCP based upon price movements of their transactions.
Trade exposures As (in Chapter 8 of this framework), includes the current and potential future exposure of a clearing member or a client to a CCP arising from over-the-counter derivatives, exchange traded derivatives transactions or securities financing transactions, as well as initial margin. For the purposes of this definition, the current exposure of a clearing member includes the variation margin due to the clearing member but not yet received.
Default funds Also known as clearing deposits or guaranty fund contributions (or any other names), are clearing members' funded or unfunded contributions towards, or underwriting of, a CCP's mutualized loss sharing arrangements. The description given by a CCP to its mutualized loss sharing arrangements is not determinative of their status as a default fund; rather, the substance of such arrangements will govern their status.
Offsetting transaction The transaction leg between the clearing member and the CCP when the clearing member acts on behalf of a client (e.g. when a clearing member clears or novates a client's trade).
Transaction types
Long settlement transactions Transactions where a counterparty undertakes to deliver a security, a commodity, or a foreign exchange amount against cash, other financial instruments, or commodities, or vice versa, at a settlement or delivery date that is contractually specified as more than the lower of the market standard for this particular instrument and five business days after the date on which the bank enters into the transaction.
Securities financing transactions (SFTs) Transactions such as repurchase agreements, reverse repurchase agreements, security lending and borrowing, and margin lending transactions, where the value of the transactions depends on market valuations and the transactions are often subject to margin agreements.
Margin lending transactions Transactions in which a bank extends credit in connection with the purchase, sale, carrying or trading of securities. Margin lending transactions do not include other loans that happen to be secured by securities collateral. Generally, in margin lending transactions, the loan amount is collateralized by securities whose value is greater than the amount of the loan.
Netting sets, hedging sets, and related terms
Netting set A group of transactions with a single counterparty that are subject to a legally enforceable bilateral netting arrangement and for which netting is recognized for regulatory capital purposes under the provisions of 6.9 and 6.10 that are applicable to the group of transactions, this framework text on credit risk mitigation techniques in credit risk mitigation techniques for exposures risk-weighted under the standardized approach of Basel III: Finalizing post-crisis reforms, or the cross product netting rules set out in 7.61 to 7.71. Each transaction that is not subject to a legally enforceable bilateral netting arrangement that is recognized for regulatory capital purposes should be interpreted as its own netting set for the purpose of these rules.
Hedging set A set of transactions within a single netting set within which full or partial offsetting is recognized for the purpose of calculating the PFE add-on of the Standardized Approach for counterparty credit risk.
Margin agreement A contractual agreement or provisions to an agreement under which one counterparty must supply variation margin to a second counterparty when an exposure of that second counterparty to the first counterparty exceeds a specified level.
Margin period of risk The largest amount of an exposure that remains outstanding until one party has the right to call for variation margin. The time period from the last exchange of collateral covering a netting set of transactions with a defaulting counterparty until that counterparty is closed out and the resulting market risk is re-hedged.
Effective maturity Under the Internal Models Method for a netting set with maturity greater than one year is the ratio of the sum of expected exposure over the life of the transactions in a netting set discounted at the risk-free rate of return divided by the sum of expected exposure over one year in a netting set discounted at the risk-free rate. This effective maturity may be adjusted to reflect rollover risk by replacing expected exposure with effective expected exposure for forecasting horizons under one year. The formula is given in 7.20.
Cross-product netting Refers to the inclusion of transactions of different product categories within the same netting set pursuant to the cross product netting rules set out in in Chapter 7 of this framework.
Distributions
Distribution of market values The forecast of the probability distribution of net market values of transactions within a netting set for some future date (the forecasting horizon) given the realized market value of those transactions up to the present time.
Distribution of exposures The forecast of the probability distribution of market values that is generated by setting forecast instances of negative net market values equal to zero (this takes account of the fact that, when the bank owes the counterparty money, the bank does not have an exposure to the counterparty).
Risk-neutral distribution A distribution of market values or exposures at a future time period where the distribution is calculated using market implied values such as implied volatilities.
Actual distribution A distribution of market values or exposures at a future time period where the distribution is calculated using historic or realized values such as volatilities calculated using past price or rate changes.
Exposure measures and adjustments
Current exposure The larger of zero, or the current market value of a transaction or portfolio of transactions within a netting set with a counterparty that would be lost upon the immediate default of the counterparty, assuming no recovery on the value of those transactions in bankruptcy. Current exposure is often also called Replacement Cost.
Peak exposure A high percentile (typically 95% or 99%) of the distribution of exposures at any particular future date before the maturity date of the longest transaction in the netting set. A peak exposure value is typically generated for many future dates up until the longest maturity date of transactions in the netting set.
Expected exposure The mean (average) of the distribution of exposures at any particular future date before the longest-maturity transaction in the netting set matures. An expected exposure value is typically generated for many future dates up until the longest maturity date of transactions in the netting set.
Effective expected exposure At a specific date is the maximum expected exposure that occurs at that date or any prior date. Alternatively, it may be defined for a specific date as the greater of the expected exposure at that date, or the effective exposure at the previous date. In effect, the Effective Expected Exposure is the Expected Exposure that is constrained to be non-decreasing over time.
Expected positive exposure(EPE) The weighted average over time of expected exposure where the weights are the proportion that an individual expected exposure represents of the entire time interval. When calculating the minimum capital requirement, the average is taken over the first year or, if all the contracts in the netting set mature before one year, over the time period of the longest-maturity contract in the netting set.
Effective expected positive exposure (Effective EPE) The weighted average over time of effective expected exposure over the first year, or, if all the contracts in the netting set mature before one year, over the time period of the longest maturity contract in the netting set where the weights are the proportion that an individual expected exposure represents of the entire time interval.
Credit valuation adjustment An adjustment to the mid-market valuation of the portfolio of trades with a counterparty. This adjustment reflects the market value of the credit risk due to any failure to perform on contractual agreements with a counterparty. This adjustment may reflect the market value of the credit risk of the counterparty or the market value of the credit risk of both the bank and the counterparty.
One-sided credit valuation adjustment A credit valuation adjustment that reflects the market value of the credit risk of the counterparty to the firm, but does not reflect the market value of the credit risk of the bank to the counterparty.
CVA Materiality Threshold The materiality threshold for CVA is where aggregate notional amount of non-centrally cleared derivatives is less than or equal to 446 billion SAR may opt not to calculate its CVA capital requirements using the SA-CVA or BA- CVA and instead choose an alternative treatment.
CCR-related risks
Rollover risk The amount by which expected positive exposure is understated when future transactions with a counterparty are expected to be conducted on an ongoing basis, but the additional exposure generated by those future transactions is not included in calculation of expected positive exposure.
General wrong-way risk Arises when the probability of default of counterparties is positively correlated with general market risk factors.
Specific wrong-way risk Arises when the exposure to a particular counterparty is positively correlated with the probability of default of the counterparty due to the nature of the transactions with the counterparty.
4. Implementation Timeline and SAMA Reporting Requirements
4.1. This framework will be effective on 01 January 2023.
4.2. SAMA expects all Banks to report the Counterparty credit risk (CCR) and Credit Valuation Adjustment (CVA) Risk-Weighted Assets (RWA) and capital charge using SAMA’s Q17 reporting template within 30 days after the end of each quarter.
Minimum Capital Requirements for Counterparty Credit Risk (CCR)
5. Counterparty Credit Risk Overview
Counterparty Credit Risk Explanation
5.1. Counterparty credit risk is defined in Chapter 3 of this framework. It is the risk that the counterparty to a transaction could default before the final settlement of the transaction in cases where there is a bilateral risk of loss. The bilateral risk of loss is the key concept on which the definition of counterparty credit risk is based and is explained further below.
5.2. When a bank makes a loan to a borrower the credit risk exposure is unilateral. That is, the bank is exposed to the risk of loss arising from the default of the borrower, but the transaction does not expose the borrower to a risk of loss from the default of the bank. By contrast, some transactions give rise to a bilateral risk of loss and therefore give rise to a counterparty credit risk charge. For example:
(1) A bank makes a loan to a borrower and receives collateral from the borrower.1
(a) The bank is exposed to the risk that the borrower defaults and the sale of the collateral is insufficient to cover the loss on the loan.
(b) The borrower is exposed to the risk that the bank defaults and does not return the collateral. Even in cases where the customer has the legal right to offset the amount it owes on the loan in compensation for the lost collateral, the customer is still exposed to the risk of loss at the outset of the loan because the value of the loan may be less than the value of the collateral the time of default of the bank.
(2) A bank borrows cash from a counterparty and posts collateral to the counterparty (or undertakes a transaction that is economically equivalent, such as the sale and repurchase (repo) of a security).
(a) The bank is exposed to the risk that its counterparty defaults and does not return the collateral that the bank posted.
(b) The counterparty is exposed to the risk that the bank defaults and the amount the counterparty raises from the sale of the collateral that the bank posted is insufficient to cover the loss on the counterparty’s loan to the bank.
(1) A bank borrows a security from a counterparty and posts cash to the counterparty as collateral (or undertakes a transaction that is economically equivalent, such as a reverse repo).
(a) The bank is exposed to the risk that its counterparty defaults and does not return the cash that the bank posted as collateral.
(b) The counterparty is exposed to the risk that the bank defaults and the cash that the bank posted as collateral is insufficient to cover the loss of the security that the bank borrowed.
(2) A bank enters a derivatives transaction with a counterparty (e.g. it enters a swap transaction or purchases an option). The value of the transaction can vary over time with the movement of underlying market factors.2
(a) The bank is exposed to the risk that the counterparty defaults when the derivative has a positive value for the bank.
(b) The counterparty is exposed to the risk that the bank defaults when the derivative has a positive value for the counterparty.
1 The bilateral risk of loss in this example arises because the bank receives, i.e. takes possession of, the collateral as part of the transaction. By contrast, collateralized loans where the collateral is not exchanged prior to default, do not give rise to a bilateral risk of loss; for example a corporate or retail loan secured on a property of the borrower where the bank may only take possession of the property when the borrower defaults does not give rise to counterparty credit risk.
2 The counterparty credit risk rules capture the risk of loss to the bank from the default of the derivative counterparty. The risk of gains or losses on the changing market value of the derivative is captured by the market risk framework. The market risk framework captures the risk that the bank will suffer a loss as a result of market movements in underlying risk factors referenced by the derivative (e.g. interest rates for an interest rate swap); however, it also captures the risk of losses that can result from the derivative declining in value due to a deterioration in the creditworthiness of the derivative counterparty. The latter risk is the credit valuation adjustment risk set out in Chapter 11 of this Framework.Scope of Counterparty Credit Risk Charge
5.3. Banks must calculate a counterparty credit risk charge for all exposures that give rise to counterparty credit risk, with the exception of those transactions listed in 5.15 below. The categories of transaction that give rise to counterparty credit risk are:
(1) Over-the-counter (OTC) derivatives
(2) Exchange-traded derivatives
(3) Long settlement transactions
(4) Securities financing transactions
5.4. The transactions listed in 5.3 above generally exhibit the following abstract characteristics:
(1) The transactions generate a current exposure or market value.
(2) The transactions have an associated random future market value based on market variables.
(3) The transactions generate an exchange of payments or an exchange of a financial instrument (including commodities) against payment.
(4) The transactions are undertaken with an identified counterparty against which a unique probability of default can be determined.
5.5. Other common characteristics of the transactions listed in 5.3 include the following:
(1) Collateral may be used to mitigate risk exposure and is inherent in the nature of some transactions.
(2) Short-term financing may be a primary objective in that the transactions mostly consist of an exchange of one asset for another (cash or securities) for a relatively short period of time, usually for the business purpose of financing. The two sides of the transactions are not the result of separate decisions but form an indivisible whole to accomplish a defined objective.
(1) Netting may be used to mitigate the risk.
(2) Positions are frequently valued (most commonly on a daily basis), according to market variables.
(3) Remargining may be employed.
Methods to Calculate Counterparty Credit Risk Exposure
5.6. For the transaction types listed in 5.3 above, banks must calculate their counterparty credit risk exposure, or exposure at default (EAD),3 using one of the methods set out in 5.7 to 5.8 below. The methods vary according to the type of the transaction, the counterparty to the transaction, and whether the bank has received SAMA approval to use the method (if such approval is required).
5.7. For exposures that are not cleared through a central counterparty (CCP) the following methods must be used to calculate the counterparty credit risk exposure:
(1) Standardized approach for measuring counterparty credit risk exposures (SACCR), which is set out in Chapter 6 of this framework. This method is to be used for exposures arising from OTC derivatives, exchange-traded derivatives and long settlement transactions. This method must be used if the bank does not have approval to use the internal models method (IMM).
(2) The simple approach or comprehensive approach to the recognition of collateral, which are both set out in the credit risk mitigation chapter of the standardized approach to credit risk (see Chapter 9 on the mitigation techniques for exposures risk-weighted under the standardized approach of the Minimum Capital Requirements for Credit Risk). These methods are to be used for securities financing transactions (SFTs) and must be used if the bank does not have approval to use the IMM.
(3) The value-at-risk (VaR) models approach, which is set out in paragraphs 73-76 of Chapter 9 of the Minimum Capital Requirements for Credit Risk. For banks applying the IRB approach to credit risk, the VaR models approach may be used to calculate EAD for SFTs, subject to SAMA approval, as an alternative to the method set out in (2) above.
(4) The IMM, which is set out in Chapter 7 of this framework. This method may be used, subject to SAMA approval, as an alternative to the methods to calculate counterparty credit risk exposures set out in (1) and (2) above (for all of the exposures referenced in those bullets).
5.8. For exposures that are cleared through a CCP, banks must apply the method set out Chapter 8 of this framework. This method covers:
(1) the exposures of a bank to a CCPs when the bank is a clearing member of the CCP;
(2) the exposures of a bank to its clients, when the bank is a clearing members and act as an intermediary between the client and the CCP; and
(3) the exposures of a bank to a clearing member of a CCP, when the bank is a client of the clearing member and the clearing member is acting as an intermediary between the bank and the CCP.
5.9. Exposures to central counterparties arising from the settlement of cash transactions (equities, fixed income, spot foreign exchange and spot commodities), are excluded from the requirements of Chapter 8 of this framework. They are instead subject to the requirements of chapter 25 of the Minimum Capital Requirements for Credit Risk.
5.10. Under the methods outlined above, the exposure amount or EAD for a given counterparty is equal to the sum of the exposure amounts or EADs calculated for each netting set with that counterparty, subject to the exception outlined in 5.11 below.
5.11. The exposure or EAD for a given OTC derivative counterparty is defined as the greater of zero and the difference between the sum of EADs across all netting sets with the counterparty and the credit valuation adjustment (CVA) for that counterparty which has already been recognized by the bank as an incurred write down (i.e. a CVA loss). This CVA loss is calculated without taking into account any offsetting debit valuation adjustments, which have been deducted from capital under the Regulatory Adjustments or “Filter” chapter of Section A of SAMA's Final Guidance Document Concerning Implementation of Capital Reforms Under Basel III Framework4. This reduction of EAD by incurred CVA losses does not apply to the determination of the CVA risk capital requirement.
3 The terms “exposure” and “EAD” are used interchangeable in the counterparty credit risk chapters of the credit risk standard. This reflects the fact that the amounts calculated under the counterparty credit risk rules must typically be used as either the “exposure” within the standardized approach to credit risk, or the EAD within the internal ratings-based (IRB) approach to credit risk, as described in 5.12.
4 SAMA circulars would be Circular No.: 341000015689, which I will be referencing in CCR Framework. Section A: Final Guidance DocumentMethods to Calculate CCR Risk-Weighted Assets
5.12. After banks have calculated their counterparty credit risk exposures, or EAD, according to the methods outlined above, they must apply the standardized approach to credit risk, the IRB approach to credit risk, or, in the case of the exposures to CCPs, the capital requirements set out in Chapter 8 of this framework. For counterparties to which the bank applies the standardized approach, the counterparty credit risk exposure amount will be risk weighted according to the relevant risk weight of the counterparty. For counterparties to which the bank applies the IRB approach, the counterparty credit risk exposure amount defines the EAD that is used within the IRB approach to determine risk- weighted assets (RWA) and expected loss amounts.
5.13. For IRB exposures, the risk weights applied to OTC derivative exposures should be calculated with the full maturity adjustment (as defined in paragraph 6 of chapter 11 of the Minimum Capital Requirements for Credit Risk) capped at 1 for each netting set for which the bank calculates CVA capital under either the basic approach (BA-CVA) or the standardized approach (SA-CVA), as provided in 11.12.
5.14. For banks that have SAMA approval to use IMM, RWA for credit risk must be calculated as the higher of:
(1) the sum of RWA calculated using Internal Models Method (IMM) with current parameter calibrations; and
(2) the sum of RWA calculated using IMM with stressed parameter calibrations.
Exemptions
5.15. As an exception to the requirements of 5.3 above, banks are not required to calculate a counterparty credit risk charge for the following types of transactions (i.e. the exposure amount or EAD for counterparty credit risk for the transaction will be zero):
(1) Credit derivative protection purchased by the bank against a banking book exposure, or against a counterparty credit risk exposure. In such cases, the bank will determine its capital requirement for the hedged exposure according to the criteria and general rules for the recognition of credit derivatives within the standardized approach or IRB approach to credit risk (i.e. substitution approach).
(2) Sold credit default swaps in the banking book where they are treated in the framework as a guarantee provided by the bank and subject to a credit risk charge for the full notional amount.
Minimum Haircut Floors for Securities Financing Transactions (SFTs)
5.16. Chapter 10 of this framework specifies the treatment of certain non-centrally cleared SFTs with certain counterparties (in-scope SFTs). The requirements are applicable to banks in jurisdictions that are permitted to conduct in-scope SFTs below the minimum haircut floors specified within Chapter 10 of this framework.
6. Standardized Approach to Counterparty Credit Risk
Overview and Scope
6.1. The Standardized Approach for Counterparty Credit Risk (SA-CCR) applies to over the-counter (OTC) derivatives, exchange-traded derivatives and long settlement transactions.5 Banks that do not have approval to apply the internal model method (IMM) for the relevant transactions must use SA-CCR, as set out in this chapter.
6.2. EAD is to be calculated separately for each netting set (as set out in 4.14 , each transaction that is not subject to a legally enforceable bilateral netting arrangement that is recognized for regulatory capital purposes should be interpreted as its own netting set).6 It is determined using the following formula, where:
(1) alpha = 1.4
(2) RC = the replacement cost calculated according to 6.5 to 6.21
(3) PFE = the amount for potential future exposure calculated according to 6.22 to 6.79
EAD = alpha * (RC + PFE)
6.3. For credit derivatives where the bank is the protection seller and that are outside netting and margin agreements, the EAD may be capped to the amount of unpaid premia. Banks have the option to remove such credit derivatives from their legal netting sets and treat them as individual unmargined transactions in order to apply the cap.
6.4. The replacement cost (RC) and the potential future exposure (PFE) components are calculated differently for margined and unmargined netting sets. Margined netting sets are netting sets covered by a margin agreement under which the bank’s counterparty has to post variation margin; all other netting sets, including those covered by a one-way margin agreement where only the bank posts variation margin, are treated as unmargined for the purposes of the SA-CCR. The EAD for a margined netting set is capped at the EAD of the same netting set calculated on an unmargined basis.
5 See chapter 12 and Chapter 13 of this framework for illustrative examples of the application of the SA-CCR to sample portfolios
6 The EAD can be set to zero only for sold options that are outside netting and margin agreements.Replacement Cost and Net Independent Collateral Amount
6.5. For unmargined transactions, the RC intends to capture the loss that would occur if a counterparty were to default and were closed out of its transactions immediately. The PFE add-on represents a potential conservative increase in exposure over a one-year time horizon from the present date (i.e. the calculation date).
6.6. For margined trades, the RC intends to capture the loss that would occur if a counterparty were to default at the present or at a future time, assuming that the closeout and replacement of transactions occur instantaneously. However, there may be a period (the margin period of risk) between the last exchange of collateral before default and replacement of the trades in the market. The PFE add-on represents the potential change in value of the trades during this time period.
6.7. In both cases, the haircut applicable to noncash collateral in the replacement cost formulation represents the potential change in value of the collateral during the appropriate time period (one year for unmargined trades and the margin period of risk for margined trades).
6.8. Replacement cost is calculated at the netting set level, whereas PFE add-ons are calculated for each asset class within a given netting set and then aggregated (see 6.26 to 6.79 below).
6.9. For capital adequacy purposes, banks may net transactions (e.g. when determining the RC component of a netting set) subject to novation under which any obligation between a bank and its counterparty to deliver a given currency on a given value date is automatically amalgamated with all other obligations for the same currency and value date, legally substituting one single amount for the previous gross obligations. Banks may also net transactions subject to any legally valid form of bilateral netting not covered in the preceding sentence, including other forms of novation. In every such case where netting is applied, a bank must satisfy SAMA that it has:
(1) A netting contract with the counterparty or other agreement which creates a single legal obligation, covering all included transactions, such that the bank would have either a claim to receive or obligation to pay only the net sum of the positive and negative mark-to-market values of included individual transactions in the event a counterparty fails to perform due to any of the following: default, bankruptcy, liquidation or similar circumstances.7
(2) Written and reasoned legal reviews that, in the event of a legal challenge, the relevant courts and administrative authorities would find the bank’s exposure to be such a net amount under:
(3) The law of the jurisdiction in which the counterparty is chartered and, if the foreign branch of a counterparty is involved, then also under the law of the jurisdiction in which the branch is located;
(a) The law that governs the individual transactions; and
(b) The law that governs any contract or agreement necessary to effect the netting.
(4) Procedures in place to ensure that the legal characteristics of netting arrangements are kept under review in light of the possible changes in relevant law.
6.10. SAMA, after consultation when necessary with other relevant supervisors, must be satisfied that the netting is enforceable under the laws of each of the relevant jurisdictions. Thus, if any of these supervisors is dissatisfied about enforceability under its laws, the netting contract or agreement will not meet this condition and neither counterparty could obtain supervisory benefit.
6.11. There are two formulations of replacement cost depending on whether the trades with a counterparty are margined or unmargined. The margined formulation could apply both to bilateral transactions and to central clearing relationships. The formulation also addresses the various arrangements that a bank may have to post and/or receive collateral that may be referred to as initial margin.
Formulation for unmargined transactions
6.12. For unmargined transactions, RC is defined as the greater of:
(i) the current market value of the derivative contracts less net haircut collateral held by the bank (if any), and
(ii) zero. This is consistent with the use of replacement cost as the measure of current exposure, meaning that when the bank owes the counterparty money it has no exposure to the counterparty if it can instantly replace its trades and sell collateral at current market prices.8
The formula for RC is as follows, where:
(1) V is the value of the derivative transactions in the netting set
(2) C is the haircut value of net collateral held, which is calculated in accordance with the net independent collateral amount (NICA) methodology defined in 6.19.9
RC = max{V - C; 0}
6.13. For the purpose of 6.12 above, the value of non-cash collateral posted by the bank to its counterparty is increased and the value of the non-cash collateral received by the bank from its counterparty is decreased using haircuts (which are the same as those that apply to repo-style transactions) for the time periods described in 6.7above.
6.14. The formulation set out in 6.12 above, does not permit the replacement cost, which represents today’s exposure to the counterparty, to be less than zero. However, banks sometimes hold excess collateral (even in the absence of a margin agreement) or have out-of-the-money trades which can further protect the bank from the increase of the exposure. As discussed in 6.23 to 6.25 below, the SA-CCR allows such over-collateralization and negative mark-to market value to reduce PFE, but they are not permitted to reduce replacement cost.
Formulation for margined transactions
6.15. The RC formula for margined transactions builds on the RC formula for unmargined transactions. It also employs concepts used in standard margining agreements, as discussed more fully below.
6.16. The RC for margined transactions in the SA-CCR is defined as the greatest exposure that would not trigger a call for VM, taking into account the mechanics of collateral exchanges in margining agreements.10 Such mechanics include, for example, “Threshold”, “Minimum Transfer Amount” and “Independent Amount” in the standard industry documentation,11 which are factored into a call for VM.12 A defined, generic formulation has been created to reflect the variety of margining approaches used and those being considered by supervisors internationally.
Incorporating NICA into replacement cost
6.17. One objective of the SA-CCR is to reflect the effect of margining agreements and the associated exchange of collateral in the calculation of CCR exposures. The following paragraphs address how the exchange of collateral is incorporated into the SA-CCR.
6.18. To avoid confusion surrounding the use of terms initial margin and independent amount which are used in various contexts and sometimes interchangeably, the term independent collateral amount (ICA) is introduced. ICA represents:
(i) collateral (other than VM) posted by the counterparty that the bank may seize upon default of the counterparty, the amount of which does not change in response to the value of the transactions it secures and/or
(ii) the Independent Amount (IA) parameter as defined in standard industry documentation. ICA can change in response to factors such as the value of the collateral or a change in the number of transactions in the netting set.
6.19. Because both a bank and its counterparty may be required to post ICA, it is necessary to introduce a companion term, net independent collateral amount (NICA), to describe the amount of collateral that a bank may use to offset its exposure on the default of the counterparty. NICA does not include collateral that a bank has posted to a segregated, bankruptcy remote account, which presumably would be returned upon the bankruptcy of the counterparty. That is, NICA represents any collateral (segregated or unsegregated) posted by the counterparty less the unsegregated collateral posted by the bank. With respect to IA, NICA takes into account the differential of IA required for the bank minus IA required for the counterparty.
6.20. For margined trades, the replacement cost is calculated using the following formula, where:
(1) V and C are defined as in the unmargined formulation, except that C now includes the net variation margin amount, where the amount received by the bank is accounted with a positive sign and the amount posted by the bank is accounted with a negative sign
(2) TH is the positive threshold before the counterparty must send the bank collateral
(3) MTA is the minimum transfer amount applicable to the counterparty
RC = max{V - C; TH + MTA - NICA; 0}
6.21. TH + MTA – NICA represents the largest exposure that would not trigger a VM call and it contains levels of collateral that need always to be maintained. For example, without initial margin or IA, the greatest exposure that would not trigger a variation margin call is the threshold plus any minimum transfer amount. In the adapted formulation, NICA is subtracted from TH + MTA. This makes the calculation more accurate by fully reflecting both the actual level of exposure that would not trigger a margin call and the effect of collateral held and /or posted by a bank. The calculation is floored at zero, recognizing that the bank may hold NICA in excess of TH + MTA, which could otherwise result in a negative replacement cost.
PFE add-on for each netting set
6.22. The PFE add-on consists of:
(i) an aggregate add-on component; and
(ii) a multiplier that allows for the recognition of excess collateral or negative mark-to-market value for the transactions within the netting set. The formula for PFE is as follows, where:
(1) AddOnaggregate is the aggregate add-on component (see 6.27 below)
(2) multiplier is defined as a function of three inputs: V, C and AddOnaggregate
PFE = multiplier * AddOnaggregate
7 The netting contract must not contain any clause which, in the event of default of a counterparty, permits a non-defaulting counterparty to make limited payments only, or no payments at all, to the estate of the defaulting party, even if the defaulting party is a net creditor.
8 The haircut applicable in the replacement cost calculation for unmargined trades should follow the formula in paragraphs 62 of chapter 9 of the Minimum Capital Requirements for Credit Risk. In applying the formula, banks must use the maturity of the longest transaction in the netting set as the value for N , capped at 250 days, in order to R scale haircuts for unmargined trades, which is capped at 100%.
9 As set out in 6.4, netting sets that include a one-way margin agreement in favor of the bank’s counterparty (i.e. the bank posts, but does not receive variation margin) are treated as unmargined for the purposes of SA-CCR. For such netting sets, C also includes, with a negative sign, the variation margin amount posted by the bank to the counterparty.
10 See chapter 12 and Chapter 13 of this framework for illustrative examples of the effect of standard margin agreements on the SA-CCR formulation.
11 For example, the 1992 (Multicurrency-Cross Border) Master Agreement and the 2002 Master Agreement published by the International Swaps & Derivatives Association, Inc. (ISDA Master Agreement). The ISDA Master Agreement includes the ISDA Credit Support Annexes: the 1994 Credit Support Annex (Security Interest – New York Law), or, as applicable, the 1995 Credit Support Annex (Transfer – English Law) and the 1995 Credit Support Deed (Security Interest – English Law).
12 For example, in the ISDA Master Agreement, the term “Credit Support Amount”, or the overall amount of collateral that must be delivered between the parties, is defined as the greater of the Secured Party’s Exposure plus the aggregate of all Independent Amounts applicable to the Pledgor minus all Independent Amounts applicable to the Secured Party, minus the Pledgor’s Threshold and zero.Multiplier (Recognition of Excess Collateral and Negative Mark-to-Market)
6.23. As a general principle, over-collateralization should reduce capital requirements for counterparty credit risk. In fact, many banks hold excess collateral (i.e. collateral greater than the net market value of the derivatives contracts) precisely to offset potential increases in exposure represented by the add-on. As discussed in 6.12 and 6.20, collateral may reduce the replacement cost component of the exposure under the SA-CCR. The PFE component also reflects the risk-reducing property of excess collateral.
6.24. Banks should apply a multiplier to the PFE component that decreases as excess collateral increases, without reaching zero (the multiplier is floored at 5% of the PFE add-on). When the collateral held is less than the net market value of the derivative contracts (“under-collateralization”), the current replacement cost is positive and the multiplier is equal to one (i.e. the PFE component is equal to the full value of the aggregate add-on). Where the collateral held is greater than the net market value of the derivative contracts (“over-collateralization”), the current replacement cost is zero and the multiplier is less than one (i.e. the PFE component is less than the full value of the aggregate add-on).
6.25. This multiplier will also be activated when the current value of the derivative transactions is negative. This is because out-of-the-money transactions do not currently represent an exposure and have less chance to go in-the-money. The formula for the multiplier is as follows, where:
(1) exp(…) is the exponential function
(2) Floor is 5%
(3) V is the value of the derivative transactions in the netting set
(4) C is the haircut value of net collateral held
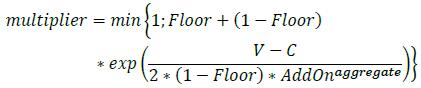
Aggregate add-on and asset classes
6.26. To calculate the aggregate add-on, banks must calculate add-ons for each asset class within the netting set. The SA-CCR uses the following five asset classes:
(1) Interest rate derivatives
(2) Foreign exchange derivatives
(3) Credit derivatives
(4) Equity derivatives.
(5) Commodity derivatives
6.27. Diversification benefits across asset classes are not recognized. Instead, the respective add-ons for each asset class are simply aggregated using the following formula (where the sum is across the asset classes):
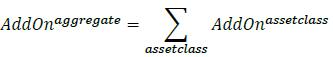
Allocation of derivative transactions to one or more asset classes
6.28. The designation of a derivative transaction to an asset class is to be made on the basis of its primary risk driver. Most derivative transactions have one primary risk driver, defined by its reference underlying instrument (e.g. an interest rate curve for an interest rate swap, a reference entity for a credit default swap, a foreign exchange rate for a foreign exchange (FX) call option, etc.). When this primary risk driver is clearly identifiable, the transaction will fall into one of the asset classes described above.
6.29. For more complex trades that may have more than one risk driver (e.g. multi-asset or hybrid derivatives), banks must take sensitivities and volatility of the underlying into account for determining the primary risk driver
6.30. SAMA may also require more complex trades to be allocated to more than one asset class, resulting in the same position being included in multiple classes. In this case, for each asset class to which the position is allocated, banks must determine appropriately the sign and delta adjustment of the relevant risk driver (the role of delta adjustments in SA-CCR is outlined further in 6.32 below).
General steps for calculating the PFE add-on for each asset class
6.31. For each transaction, the primary risk factor or factors need to be determined and attributed to one or more of the five asset classes: interest rate, foreign exchange, credit, equity or commodity. The add-on for each asset class is calculated using asset-class-specific formulas.13
6.32. Although the formulas for the asset class add-ons vary between asset classes, they all use the following general steps:
(6) The effective notional (D) must be calculated for each derivative (i.e. each individual trade) in the netting set. The effective notional is a measure of the sensitivity of the trade to movements in underlying risk factors (i.e. interest rates, exchange rates, credit spreads, equity prices and commodity prices). The effective notional is calculated as the product of the following parameters (i.e. D = d * MF * δ):
(a) The adjusted notional (d). The adjusted notional is a measure of the size of the trade. For derivatives in the foreign exchange asset class this is simply the notional value of the foreign currency leg of the derivative contract, converted to the Saudi Riyal (SAR). For derivatives in the equity and commodity asset classes, it is simply the current price of the relevant share or unit of commodity multiplied by the number of shares /units that the derivative references. For derivatives in the interest rate and credit asset classes, the notional amount is adjusted by a measure of the duration of the instrument to account for the fact that the value of instruments with longer durations are more sensitive to movements in underlying risk factors (i.e. interest rates and credit spreads).
(b) The maturity factor (MF). The maturity factor is a parameter that takes account of the time period over which the potential future exposure is calculated. The calculation of the maturity factor varies depending on whether the netting set is margined or unmargined.
(c) The supervisory delta (δ). The supervisory delta is used to ensure that the effective notional take into account the direction of the trade, i.e. whether the trade is long or short, by having a positive or negative sign. It is also takes into account whether the trade has a non-linear relationship with the underlying risk factor (which is the case for options and collateralized debt obligation tranches).
(7) A supervisory factor (SF) is identified for each individual trade in the netting set. The supervisory factor is the supervisory specified change in value of the underlying risk factor on which the potential future exposure calculation is based, which has been calibrated to take into account the volatility of underlying risk factors.
(8) The trades within each asset class are separated into supervisory specified hedging sets. The purpose of the hedging sets is to group together trades within the netting set where long and short positions should be permitted to offset each other in the calculation of potential future exposure.
(9) Aggregation formulas are applied to aggregate the effective notionals and supervisory factors across all trades within each hedging set and finally at the asset-class level to give the asset class level add-on. The method of aggregation varies between asset classes and for credit, equity and commodity derivatives it also involves the application of supervisory correlation parameters to capture diversification of trades and basis risk.
Time period parameters: Mi, Ei, Si and Ti
6.33. There are four time period parameters that are used in the SA-CCR (all expressed in years):
(1) For all asset classes, the maturity Mi of a contract is the time period (starting today) until the latest day when the contract may still be active. This time period appears in the maturity factor defined in 6.51 to 6.56 that scales down the adjusted notionals for unmargined trades for all asset classes. If a derivative contract has another derivative contract as its underlying (for example, a swaption) and may be physically exercised into the underlying contract (i.e. a bank would assume a position in the underlying contract in the event of exercise), then maturity of the contract is the time period until the final settlement date of the underlying derivative contract.
(2) For interest rate and credit derivatives, Siis the period of time (starting today) until start of the time period referenced by an interest rate or credit contract. If the derivative references the value of another interest rate or credit instrument (e.g. swaption or bond option), the time period must be determined on the basis of the underlying instrument. Si appears in the definition of supervisory duration defined in 6.36.
(3) For interest rate and credit derivatives, Ei is the period of time (starting today) until the end of the time period referenced by an interest rate or credit contract. If the derivative references the value of another interest rate or credit instrument (e.g. swaption or bond option), the time period must be determined on the basis of the underlying instrument. Ei appears in the definition of supervisory duration defined in 6.36. In addition, Ei is used for allocating derivatives in the interest rate asset class to maturity buckets, which are used in the calculation of the asset class add-on (see 6.60(3)).
(4) For options in all asset classes, Ti is the time period (starting today) until the latest contractual exercise date as referenced by the contract. This period shall be used for the determination of the option’s supervisory delta in 6.40 to 6.43.
6.34. Table 1 includes example transactions and provides each transaction’s related maturity Mi, start date Si and end date Ei. In addition, the option delta in 6.40 to 6.43 depends on the latest contractual exercise date Ti (not separately shown in the table).
Table 1: Example transactions and related (maturity Mi, start date Si and end date Ei) Instrument Mi Si Ei Interest rate or credit default swap maturing in 10 years 10 years 0 10 years 10-year interest rate swap, forward starting in 5 years 15 years 5 years 15 years Forward rate agreement for time period starting in 6 months and ending in 12 months 1 year 0.5 year 1 years Cash-settled European swaption referencing 5-year interest rate swap with exercise date in 6 months 0.5 year 0.5 year 5.5 year Physically-settled European swaption referencing 5-year interest rate swap with exercise date in 6 months 5.5 years 0.5 year 5.5 years 10-year Bermudan swaption with annual exercise dates 10 years 1 year 10 years Interest rate cap or floor specified for semiannual interest rate with maturity 5 years 5 years 0 5 years Option on a bond maturing in 5 years with the latest exercise date in 1 year 1 year 1 year 5 years 3-month Eurodollar futures that matures in 1 year 1 year 1 year 1.25 years Futures on 20-year treasury bond that matures in 2 years 2 years 2 years 22 years 6-month option on 2-year futures on 20-year treasury bond 2 years 2 years 22 years Trade-level adjusted notional (for trade i): di
6.35. The adjusted notionals are defined at the trade level and take into account both the size of a position and its maturity dependency, if any.
6.36. For interest rate and credit derivatives, the trade-level adjusted notional is the product of the trade notional amount, converted to the Saudi Riyal (SAR), and the supervisory duration SD, which is given by the formula below (i.e.di = notional * SDi). The calculated value of SDi is floored at ten business days.14 If the start date has occurred (e.g. an ongoing interest rate swap), Si must be set to zero.
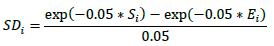
6.37. For foreign exchange derivatives, the adjusted notional is defined as the notional of the foreign currency leg of the contract, converted to the Saudi Riyal (SAR). If both legs of a foreign exchange derivative are denominated in currencies other than the Saudi Riyal (SAR), the notional amount of each leg is converted to the Saudi Riyal (SAR) and the leg with the larger Saudi Riyal (SAR) value is the adjusted notional amount.
6.38. For equity and commodity derivatives, the adjusted notional is defined as the product of the current price of one unit of the stock or commodity (e.g. a share of equity or barrel of oil) and the number of units referenced by the trade.
6.39. In many cases the trade notional amount is stated clearly and fixed until maturity. When this is not the case, banks must use the following rules to determine the trade notional amount.
(1) Where the notional is a formula of market values, the bank must enter the current market values to determine the trade notional amount.
(2) For all interest rate and credit derivatives with variable notional amounts specified in the contract (such as amortizing and accreting swaps), banks must use the average notional over the remaining life of the derivative as the trade notional amount. The average should be calculated as “time weighted”. The averaging described in this paragraph does not cover transactions where the notional varies due to price changes (typically, FX, equity and commodity derivatives).
(3) Leveraged swaps must be converted to the notional of the equivalent unleveraged swap, that is, where all rates in a swap are multiplied by a factor, the stated notional must be multiplied by the factor on the interest rates to determine the trade notional amount.
(4) For a derivative contract with multiple exchanges of principal, the notional is multiplied by the number of exchanges of principal in the derivative contract to determine the trade notional amount.
(5) For a derivative contract that is structured such that on specified dates any outstanding exposure is settled and the terms are reset so that the fair value of the contract is zero, the remaining maturity equals the time until the next reset date.
Supervisory delta adjustment
6.40. The supervisory delta adjustment (δi) parameters are also defined at the trade i level and are applied to the adjusted notional amounts to reflect the direction of the transaction and its non-linearity.15
6.41. The delta adjustments for all instruments that are not options and are not collateralized debt obligation (CDO) tranches are as set out in the table below:16
δi Long in the primary risk factor Short in the primary risk factor Instruments that are not options or CDO tranches +1 -1 6.42. The delta adjustments for options are set out in the table below, where:
(1) The following are parameters that banks must determine appropriately:
(a) Pi: Underlying price (spot, forward, average, etc.)
(b) Ki: Strike price
(c) Ti: Latest contractual exercise date of the option
(2) The supervisory volatility σi an option is specified on the basis of supervisory factor applicable to the trade (see Table 2 in 6.75).
(3) The symbol Φ represents the standard normal cumulative distribution function.
δi Bought Sold Call Option 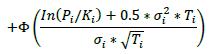
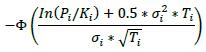
Put Option 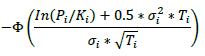
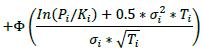
Delta (δ) Bought Sold Call Option 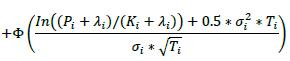
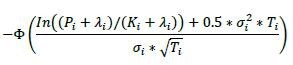
Put Option 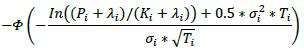
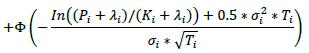
6.43. The delta adjustments for CDO tranches17 are set out in the table below, where the following are parameters that banks must determine appropriately:
(1) Ai: Attachment point of the CDO tranche
(2) Di: Detachment point of the CDO tranche
δi Purchased (long protection) Sold (Short protection) CDO tranche s 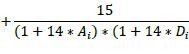
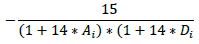
Effective notional for options
6.44. For single-payment options the effective notional (i.e. D = d * MF * δ) is calculated using the following specifications:
(1) For European, Asian, American and Bermudan put and call options, the supervisory delta must be calculated using the simplified Black-Scholes formula referenced in 6.42. In the case of Asian options, the underlying price must be set equal to the current value of the average used in the payoff. In the case of American and Bermudan options, the latest allowed exercise date must be used as the exercise date Ti in the formula.
(2) For Bermudan swaptions, the start date Si must be equal to the earliest allowed exercise date, while the end date Ei must be equal to the end date of the underlying swap.
(3) For digital options, the payoff of each digital option (bought or sold) with strike Ki must be approximated via the “collar” combination of bought and sold European options of the same type (call or put), with the strikes set equal to 0.95.Ki and 1.05.Ki. The size of the position in the collar components must be such that the digital payoff is reproduced exactly outside the region between the two strikes. The effective notional is then computed for the bought and sold European components of the collar separately, using the option formulae for the supervisory delta referenced in 6.42 (the exercise date Tiand the current value of the underlying Pi of the digital option must be used). The absolute value of the digital-option effective notional must be capped by the ratio of the digital payoff to the relevant supervisory factor.
(4) If a trade’s payoff can be represented as a combination of European option payoffs (e.g. collar, butterfly/calendar spread, straddle, strangle), each European option component must be treated as a separate trade.
6.45. For the purposes of effective notional calculations, multiple-payment options may be represented as a combination of single-payment options. In particular, interest rate caps/floors may be represented as the portfolio of individual caplets /floorlets, each of which is a European option on the floating interest rate over a specific coupon period. For each caplet/floorlet, Si and Tiare the time periods starting from the current date to the start of the coupon period, while Ei is the time period starting from the current date to the end of the coupon period.
6.46. In the case of options (e.g. interest rate caps/floors that may be represented as the portfolio of individual caplets/floorlets), banks may decompose those products in a manner consistent with 6.45. Banks may not decompose linear products (e.g. ordinary interest rate swaps).
Supervisory factors: SFi
6.47. Supervisory factors (SFi) are used, together with aggregation formulas, to convert effective notional amounts into the add-on for each hedging set.18 The way in which supervisory factors are used within the aggregation formulas varies between asset classes. The supervisory factors are listed in Table 2 under 6.75.
Hedging sets
6.48. The hedging sets in the different asset classes are defined as follows, except for those described in 6.49 and 6.50:
(1) Interest rate derivatives consist of a separate hedging set for each currency.
(2) FX derivatives consist of a separate hedging set for each currency pair.
(3) Credit derivatives consist of a single hedging set.
(4) Equity derivatives consist of a single hedging set.
(5) Commodity derivatives consist of four hedging sets defined for broad categories of commodity derivatives: energy, metals, agricultural and other commodities.
6.49. Derivatives that reference the basis between two risk factors and are denominated in a single currency19 (basis transactions) must be treated within separate hedging sets within the corresponding asset class. There is a separate hedging set20 for each pair of risk factors (i.e. for each specific basis). Examples of specific bases include three-month Libor versus six-month Libor, three-month Libor versus three-month T-Bill, one-month Libor versus overnight indexed swap rate, Brent Crude oil versus Henry Hub gas. For hedging sets consisting of basis transactions, the supervisory factor applicable to a given asset class must be multiplied by one-half.
6.50. Derivatives that reference the volatility of a risk factor (volatility transactions) must be treated within separate hedging sets within the corresponding asset class. Volatility hedging sets must follow the same hedging set construction outlined in 6.48 (for example, all equity volatility transactions form a single hedging set). Examples of volatility transactions include variance and volatility swaps, options on realized or implied volatility. For hedging sets consisting of volatility transactions, the supervisory factor applicable to a given asset class must be multiplied by a factor of five.21
Maturity factors
6.51. The minimum time risk horizon for an unmargined transaction is the lesser of one year and the remaining maturity of the derivative contract, floored at ten business days.22 Therefore, the calculation of the effective notional for an unmargined transaction includes the following maturity factor, where Mi is the remaining maturity of transaction i, floored at 10 business days:
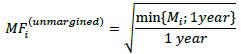
6.52. The maturity parameter (Mi) is expressed in years but is subject to a floor of 10 business days. Banks should use standard market convention to convert business days into years, and vice versa. For example, 250 business days in a year, which results in a floor of 10/250 years for Mi.
6.53. For margined transactions, the maturity factor is calculated using the margin period of risk (MPOR), subject to specified floors. That is, banks must first estimate the margin period of risk (as defined in 4.17) for each of their netting sets. They must then use the higher of their estimated margin period of risk and the relevant floor in the calculation of the maturity factor (6.55). The floors for the margin period of risk are as follows:
(1) Ten business days for non-centrally-cleared transactions subject to daily margin agreements.
(2) The sum of nine business days plus the re-margining period for non-centrally cleared transactions that are not subject daily margin agreements.
(3) The relevant floors for centrally cleared transactions are prescribed in the capital requirements for bank exposures to central counterparties (see in Chapter 8 of this framework).
6.54. The following are exceptions to the floors on the minimum margin period of risk set out in 6.53 above:
(1) For netting sets consisting of more than 5000 transactions that are not with a central counterparty the floor on the margin period of risk is 20 business days.
(2) For netting sets containing one or more trades involving either illiquid collateral, or an OTC derivative that cannot be easily replaced, the floor on the margin period of risk is 20 business days. For these purposes, "Illiquid collateral" and "OTC derivatives that cannot be easily replaced" must be determined in the context of stressed market conditions and will be characterized by the absence of continuously active markets where a counterparty would, within two or fewer days, obtain multiple price quotations that would not move the market or represent a price reflecting a market discount (in the case of collateral) or premium (in the case of an OTC derivative). Examples of situations where trades are deemed illiquid for this purpose include, but are not limited to, trades that are not marked daily and trades that are subject to specific accounting treatment for valuation purposes (e.g. OTC derivatives transactions referencing securities whose fair value is determined by models with inputs that are not observed in the market).
(3) If a bank has experienced more than two margin call disputes on a particular netting set over the previous two quarters that have lasted longer than the applicable margin period of risk (before consideration of this provision), then the bank must reflect this history appropriately by doubling the applicable supervisory floor on the margin period of risk for that netting set for the subsequent two quarters.
(4) In the case of non-centrally cleared derivatives that are subject to the requirements under Margin requirements, 6.55(3) applies only to variation margin call disputes.
6.55. The calculation of the effective notional for a margined transaction includes the following maturity factor, where MPORi is the margin period of risk appropriate for the margin agreement containing the transaction i (subject to the floors set out in 6.53 and 6.54 above).
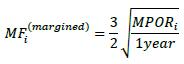
6.56. The margin period of risk (MPORi) is often expressed in days, but the calculation of the maturity factor for margined netting sets references 1 year in the denominator. Banks should use standard market convention to convert business days into years, and vice versa. For example, 1 year can be converted into 250 business days in the denominator of the MF formula if MPOR is expressed in business days. Alternatively, the MPOR expressed in business days can be converted into years by dividing it by 250.
Supervisory correlation parameters
6.57. The supervisory correlation parameters (ρi) only apply to the PFE add-on calculation for equity, credit and commodity derivatives, and are set out in Table 2 under 6.75. For these asset classes, the supervisory correlation parameters are derived from a single-factor model and specify the weight between systematic and idiosyncratic components. This weight determines the degree of offset between individual trades, recognizing that imperfect hedges provide some, but not perfect, offset. Supervisory correlation parameters do not apply to interest rate and foreign exchange derivatives.
Asset class level add-ons
6.58. As set out in 6.27, the aggregate add-on for a netting set (AddOnaggregate) is calculated as the sum of the add-ons calculated for each asset class within the netting set. The sections that follow set out the calculation of the add-on for each asset class.
Add-on for interest rate derivatives
6.59. The calculation of the add-on for the interest rate derivative asset class captures the risk of interest rate derivatives of different maturities being imperfectly correlated. It does this by allocating trades to maturity buckets, in which full offsetting of long and short positions is permitted, and by using an aggregation formula that only permits limited offsetting between maturity buckets. This allocation of derivatives to maturity buckets and the process of aggregation (steps 3 to 5 below) are only used in the interest rate derivative asset class.
6.60. The add-on for the interest rate derivative asset class (AddOnIR) within a netting set is calculated using the following steps:
(1) Step 1: Calculate the effective notional for each trade in the netting set that is in the interest rate derivative asset class. This is calculated as the product of the following three terms:
(i) the adjusted notional of the trade (d);
(ii) the supervisory delta adjustment of the trade (S); and
(iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di= di* MFi* δi, where each term is as defined in 6.35 to 6.56.
(2) Step 2: Allocate the trades in the interest rate derivative [including inflation derivatives] asset class to hedging sets. In the interest rate derivative asset class the hedging sets consist of all the derivatives that reference the same currency.
(3) Step 3: Within each hedging set allocate each of the trades to the following three maturity buckets: less than one year (bucket 1), between one and five years (bucket 2) and more than five years (bucket 3).
(4) Step 4: Calculate the effective notional of each maturity bucket by adding together all the trade level effective notionals calculated in step 1 of the trades within the maturity bucket. Let DB1, DB1 and DB1 be the effective notionals of buckets 1, 2 and 3 respectively.
(5) Step 5: Calculate the effective notional of the hedging set (ENHS ) by using either of the two following aggregation formulas (the latter is to be used if the bank chooses not to recognize offsets between long and short positions across maturity buckets):
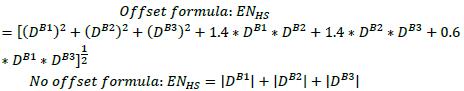
(6) Step 6: Calculate the hedging set level add-on (AddOnHS) by multiplying the effective notional of the hedging set (ENHS) by the prescribed supervisory factor (SFHS). The prescribed supervisory factor in the interest rate asset class is set at 0.5%, which means that AddOnHS= ENHS * 0.005.
(7) Step 7: Calculate the asset class level add-on (AddOnIR) by adding together all of the hedging set level add-ons calculated in step 6:
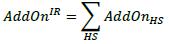
Add-on for foreign exchange derivatives
6.61. The steps to calculate the add-on for the foreign exchange derivative asset class are similar to the steps for the interest rate derivative asset class, except that there is no allocation of trades to maturity buckets (which means that there is full offsetting of long and short positions within the hedging sets of the foreign exchange derivative asset class).
6.62. The add-on for the foreign exchange derivative asset class (AddOnFX) within a netting set is calculated using the following steps:
(1) Step 1: Calculate the effective notional for each trade in the netting set that is in the foreign exchange derivative asset class. This is calculated as the product of the following three terms: (i) the adjusted notional of the trade (d); (ii) the supervisory delta adjustment of the trade (δ); and (iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di = di* MFi * δi, where each term is as defined in 6.35 to 6.56.
(2) Step 2: Allocate the trades in the foreign exchange derivative asset class to hedging sets. In the foreign exchange derivative asset class the hedging sets consist of all the derivatives that reference the same currency pair.
(3) Step 3: Calculate the effective notional of each hedging set (ENHS) by adding together the trade level effective notionals calculated in step 1.
(4) Step 4: Calculate the hedging set level add-on (AddOnHS) by multiplying the HS absolute value of the effective notional of the hedging set (ENHS) by the HS prescribed supervisory factor (SFHS). The prescribed supervisory factor in the HS foreign exchange derivative asset class is set at 4%, which means that AddOnHS= |ENHS| * 0.04.
(5) Step 5: Calculate the asset class level add-on (AddOnFX) by adding together all of the hedging set level add-ons calculated in step 5:
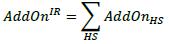
Add-on for credit derivatives
6.63. The calculation of the add-on for the credit derivative asset class only gives full recognition of the offsetting of long and short positions for derivatives that reference the same entity (e.g. the same corporate issuer of bonds). Partial offsetting is recognized between derivatives that reference different entities in step 4 below. The formula used in step 4 is explained further in 6.65 to 6.67.
6.64. The add-on for the credit derivative asset class (AddOnCredlt ) within a netting set is calculated using the following steps:
(1) Step 1: Calculate the effective notional for each trade in the netting set that is in the credit derivative asset class. This is calculated as the product of the following three terms:
(i) the adjusted notional of the trade (d);
(ii) the supervisory delta adjustment of the trade (δ); and
(iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di= di* MFi * δi, where each term is as defined in 6.35 to 6.56.
(2) Step 2: Calculate the combined effective notional for all derivatives that reference the same entity. Each separate credit index that is referenced by derivatives in the credit derivative asset class should be treated as a separate entity. The combined effective notional of the entity (ENentity) is calculated by adding together the trade level effective notionals calculated in step 1 that reference that entity.
(3) Step 3: Calculate the add-on for each entity (AddOnentity) by multiplying the entity combined effective notional for that entity calculated in step 2 by the supervisory factor that is specified for that entity (SFentity). The supervisory entity factors vary according to the credit rating of the entity in the case of single name derivatives, and whether the index is considered investment grade or non-investment grade in the case of derivatives that reference an index. The supervisory factors are set out in Table 2 in 6.75.
(4) Step 4: Calculate the asset class level add-on (AddOnCredlt) by using the formula that follows. In the formula the summations are across all entities referenced by the derivatives, AddOnentity is the add-on amount calculated entity in step 3 for each entity referenced by the derivatives and ρ is the entity supervisory prescribed correlation factor corresponding to the entity. As set out in Table 2 in 6.75, the correlation factor is 50% for single entities and 80% for indices.
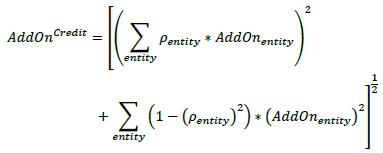
6.65. The formula to recognize partial offsetting in 6.64(4) above, is a single-factor model, which divides the risk of the credit derivative asset class into a systematic component and an idiosyncratic component. The entity-level add-ons are allowed to offset each other fully in the systematic component; whereas, there is no offsetting benefit in the idiosyncratic component. These two components are weighted by a correlation factor which determines the degree of offsetting / hedging benefit within the credit derivatives asset class. The higher the correlation factor, the higher the importance of the systematic component, hence the higher the degree of offsetting benefits.
6.66. It should be noted that a higher or lower correlation does not necessarily mean a higher or lower capital requirement. For portfolios consisting of long and short credit positions, a high correlation factor would reduce the charge. For portfolios consisting exclusively of long positions (or short positions), a higher correlation factor would increase the charge. If most of the risk consists of systematic risk, then individual reference entities would be highly correlated and long and short positions should offset each other. If, however, most of the risk is idiosyncratic to a reference entity, then individual long and short positions would not be effective hedges for each other.
6.67. The use of a single hedging set for credit derivatives implies that credit derivatives from different industries and regions are equally able to offset the systematic component of an exposure, although they would not be able to offset the idiosyncratic portion. This approach recognizes that meaningful distinctions between industries and/or regions are complex and difficult to analyze for global conglomerates.
Add-on for equity derivatives
6.68. The calculation of the add-on for the equity derivative asset class is very similar to the calculation of the add-on for the credit derivative asset class. It only gives full recognition of the offsetting of long and short positions for derivatives that reference the same entity (e.g. the same corporate issuer of shares). Partial offsetting is recognized between derivatives that reference different entities in step 4 below.
6.69. The add-on for the equity derivative asset class (AddOnEquity) within a netting set is calculated using the following steps:
(1) Step 1: Calculate the effective notional for each trade in the netting set that is in the equity derivative asset class. This is calculated as the product of the following three terms:
(i) the adjusted notional of the trade (d);
(ii) the supervisory delta adjustment of the trade (δ); and
(iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di= di* MFi* δi, where each term is as defined in 6.35 to 6.56.
(2) Step 2: Calculate the combined effective notional for all derivatives that reference the same entity. Each separate equity index that is referenced by derivatives in the equity derivative asset class should be treated as a separate entity. The combined effective notional of the entity (ENentity) is calculated entity by adding together the trade level effective notionals calculated in step 1 that reference that entity.
(3) Step 3: Calculate the add-on for each entity (AddOnentity) by multiplying the entity combined effective notional for that entity calculated in step 2 by the supervisory factor that is specified for that entity (SFentity). The supervisory entity factors are set out in Table 2 in 6.75 and vary according to whether the entity is a single name (SFentity = 32%) or an index (SFentity = 20%).
(4) Step 4: Calculate the asset class level add-on (AddOnEquity) by using the formula that follows. In the formula the summations are across all entities referenced by the derivatives, AddOnentity is the add-on amount calculated entity in step 3 for each entity referenced by the derivatives and ρentity is the entity supervisory prescribed correlation factor corresponding to the entity. As set out in Table 2 in 6.75, the correlation factor is 50% for single entities and 80% for indices.
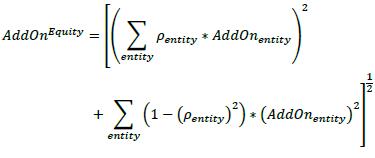
6.70. The supervisory factors for equity derivatives were calibrated based on estimates of the market volatility of equity indices, with the application of a conservative beta factor23 to translate this estimate into an estimate of individual volatilities.
6.71. Banks are not permitted to make any modelling assumptions in the calculation of the PFE add-ons, including estimating individual volatilities or taking publicly available estimates of beta. This is a pragmatic approach to ensure a consistent implementation across jurisdictions but also to keep the add-on calculation relatively simple and prudent. Therefore, bank must only use the two values of supervisory factors that are defined for equity derivatives, one for single entities and one for indices.
Add-on for commodity derivatives
6.72. The calculation of the add-on for the commodity derivative asset class is similar to the calculation of the add-on for the credit and equity derivative asset classes. It recognizes the full offsetting of long and short positions for derivatives that reference the same type of underlying commodity. It also allows partial offsetting between derivatives that reference different types of commodity, however, this partial offsetting is only permitted within each of the four hedging sets of the commodity derivative asset class, where the different commodity types are more likely to demonstrate some stable, meaningful joint dynamics. Offsetting between hedging sets is not recognized (e.g., a forward contract on crude oil cannot hedge a forward contract on corn).
6.73. The add-on for the commodity derivative asset class (AddOnCommodlty) within a netting set is calculated using the following steps:
(1) Step 1: Calculate the effective notional for each trade in the netting set that is in the commodity derivative asset class. This is calculated as the product of the following three terms:
(i) the adjusted notional of the trade (d);
(ii) the supervisory delta adjustment of the trade (δ); and
(iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di— di * MFi * δi, where each term is as defined in 6.35 to 6.56.
(2) Step 2: Allocate the trades in commodity derivative asset class to hedging sets. In the commodity derivative asset class there are four hedging sets consisting of derivatives that reference: energy, metals, agriculture and other commodities.
(3) Step 3: Calculate the combined effective notional for all derivatives with each hedging set that reference the same commodity type (e.g. all derivative that reference copper within the metals hedging set). The combined effective notional of the commodity type (ENComTyoe) is calculated by adding ComType together the trade level effective notionals calculated in step 1 that reference that commodity type.
(4) Step 4: Calculate the add-on for each commodity type (AddOnComType) within each hedging set by multiplying the combined effective notional for that commodity calculated in step 3 by the supervisory factor that is specified for that commodity type (SFComType). The supervisory factors are ComType set out in Table 2 in 6.75 and are set at 40% for electricity derivatives and 18% for derivatives that reference all other types of commodities.
(5) Step 5: Calculate the add-on for each of the four commodity hedging sets (AddOnHS) by using the formula that follows. In the formula the summations are across all commodity types within the hedging set, AddOnComType is the add-on amount ComType calculated in step 4 for each commodity type and ρComTyoe is the supervisory ComType prescribed correlation factor corresponding to the commodity type. As set out in Table 2 in 6.75, the correlation factor is set at 40% for all commodity types.
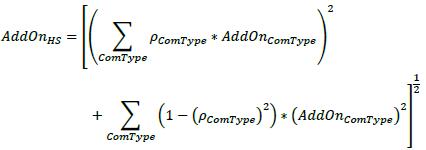
(6) Step 6: Calculate the asset class level add-on (AddOnCommodlty) by adding together all of the hedging set level add-ons calculated in step 5:
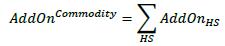
6.74. Regarding the calculation steps above, defining individual commodity types is operationally difficult. In fact, it is impossible to fully specify all relevant distinctions between commodity types so that all basis risk is captured. For example crude oil could be a commodity type within the energy hedging set, but in certain cases this definition could omit a substantial basis risk between different types of crude oil (West Texas Intermediate, Brent, Saudi Light, etc.) Also, the four commodity type hedging sets have been defined without regard to characteristics such as location and quality. For example, the energy hedging set contains commodity types such as crude oil, electricity, natural gas and coal. SAMA may require banks to use more refined definitions of commodities when they are significantly exposed to the basis risk of different products within those commodity types.
Supervisory specified parameters
6.75. Table 2 includes the supervisory factors, correlations and supervisory option volatility add-ons for each asset class and subclass.
Table 2: Summary table of supervisory parameters Asset Class Subclass Supervisory factor Correlation Supervisory option volatility Interest rate 0.50% N/A 50% Foreign exchange 4.0% N/A 15% Credit, Single Name AAA 0.38% 50% 100% AA 0.38% 50% 100% A 0.42% 50% 100% BBB 0.54% 50% 100% BB 1.06% 50% 100% B 1,6% 50% 100% CCC 6.0% 50% 100% Credit, Index IG 0.38% 80% 80% SG 1.06% 80% 80% Equity, Single Name 32% 50% 120% Equity, Index 20% 80% 75% Commodity Electricity 40% 40% 150% Oil/Gas 18% 40% 70% Metals 18% 40% 70% Agricultural 18% 40% 70% Other 18% 40% 70% 6.76. For a hedging set consisting of basis transactions, the supervisory factor applicable to its relevant asset class must be multiplied by one-half. For a hedging set consisting of volatility transactions, the supervisory factor applicable to its relevant asset class must be multiplied by a factor of five.
Treatment of multiple margin agreements and multiple netting sets
6.77. If multiple margin agreements apply to a single netting set, the netting set must be divided into sub-netting sets that align with their respective margin agreement. This treatment applies to both RC and PFE components.
6.78. If a single margin agreement applies to several netting sets, special treatment is necessary because it is problematic to allocate the common collateral to individual netting sets. The replacement cost at any given time is determined by the sum of two terms. The first term is equal to the unmargined current exposure of the bank to the counterparty aggregated across all netting sets within the margin agreement reduced by the positive current net collateral (i.e. collateral is subtracted only when the bank is a net holder of collateral). The second term is non-zero only when the bank is a net poster of collateral: it is equal to the current net posted collateral (if there is any) reduced by the unmargined current exposure of the counterparty to the bank aggregated across all netting sets within the margin agreement. Net collateral available to the bank should include both VM and NICA. Mathematically, RC for the entire margin agreement is calculated as follows, where:
(1) where the summation NS ϵ MA is across the netting sets covered by the margin agreement (hence the notation)
(2) V is the current mark-to-market value of the netting set NS and CMA is the cash equivalent value of all currently available collateral under the margin agreement
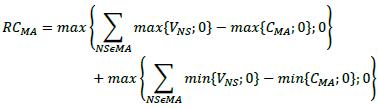
6.79. Where a single margin agreement applies to several netting sets as described in 6.78 above, collateral will be exchanged based on mark-to-market values that are netted across all transactions covered under the margin agreement, irrespective of netting sets. That is, collateral exchanged on a net basis may not be sufficient to cover PFE. In this situation, therefore, the PFE add-on must be calculated according to the unmargined methodology. Netting set-level PFEs are then aggregated using the following formula, where is the 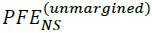 addon for the netting set NS calculated according to the unmargined requirements:
addon for the netting set NS calculated according to the unmargined requirements:
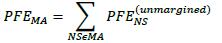
Treatment of collateral taken outside of netting sets
6.80. Eligible collateral which is taken outside a netting set, but is available to a bank to offset losses due to counterparty default on one netting set only, should be treated as an independent collateral amount associated with the netting set and used within the calculation of replacement cost under 6.12 when the netting set is unmargined and under 6.20 when the netting set is margined. Eligible collateral which is taken outside a netting set, and is available to a bank to offset losses due to counterparty default on more than one netting set, should be treated as collateral taken under a margin agreement applicable to multiple netting sets, in which case the treatment under 6.78 and 6.79 applies. If eligible collateral is available to offset losses on non-derivatives exposures as well as exposures determined using the SA-CCR, only that portion of the collateral assigned to the derivatives may be used to reduce the derivatives exposure.
13 The formulas for calculating the asset class add-ons represent stylized Effective EPE calculations under the assumption that all trades in the asset class have zero current mark-to-market value (i.e. they are at-the-money).
14 Note there is a distinction between the time period of the underlying transaction and the remaining maturity of the derivative contract. For example, a European interest rate swaption with expiry of 1 year and the term of the underlying swap of 5 years has S = 1 year and E = 6 i years.
15 Whenever appropriate, the forward (rather than spot) value of the underlying in the supervisory delta adjustments formula should be used in order to account for the risk-free rate as well as for possible cash flows prior to the option expiry (such as dividends).
16 “Long in the primary risk factor” means that the market value of the instrument increases when the value of the primary risk factor increases. “Short in the primary risk factor” means that the market value of the instrument decreases when the value of the primary risk factor increases.
17 First-to-default, second-to-default and subsequent-to-default credit derivative transactions should be treated as CDO tranches under SACCR. For an nth-to-default transaction on a pool of m reference names, banks must use an attachment point of A=(n–1)/m and a detachment point of D=n/m in order to calculate the supervisory delta formula set out 6.43.
18 Each factor has been calibrated to result in an add-on that reflects the Effective EPE of a single at- the-money linear trade of unit notional and one-year maturity. This includes the estimate of realized volatilities assumed by supervisors for each underlying asset class.
19 Derivatives with two floating legs that are denominated in different currencies (such as cross-currency swaps) are not subject to this treatment; rather, they should be treated as non-basis foreign exchange contracts.
20 Within this hedging set, long and short positions are determined with respect to the basis.
21 For equity and commodity volatility transactions, the underlying volatility or variance referenced by the transaction should replace the unit price and contractual notional should replace the number of units.
22 For example, remaining maturity for a one-month option on a 10-year Treasury bond is the one-month to expiration date of the derivative contract. However, the end date of the transaction is the 10- year remaining maturity on the Treasury bond.
23 The beta of an individual equity measures the volatility of the stock relative to a broad market index. A value of beta greater than one means the individual equity is more volatile than the index. The greater the beta is, the more volatile the stock. The beta is calculated by running a linear regression of the stock on the broad index.7. Internal Models Method for Counterparty Credit Risk
Approval to Adopt an Internal Models Method to Estimate EAD
7.1. A bank that wishes to adopt an internal models method to measure exposure or exposure at default (EAD) for regulatory capital purposes must seek SAMA approval. The internal models method is available both for banks that adopt the internal ratings-based approach to credit risk and for banks for which the standardized approach to credit risk applies to all of their credit risk exposures. The bank must meet all of the requirements given in 7.6 to 7.60 and must apply the method to all of its exposures that are subject to counterparty credit risk, except for long settlement transactions.
7.2. A bank may also choose to adopt an internal models method to measure counterparty credit risk (CCR) for regulatory capital purposes for its exposures or EAD to only over-the-counter (OTC) derivatives, to only securities financing transactions (SFTs), or to both, subject to the appropriate recognition of netting specified in 7.61 to 7.71. The bank must apply the method to all relevant exposures within that category, except for those that are immaterial in size and risk. During the initial implementation of the internal models method, a bank may use the Standardized Approach for counterparty credit risk for a portion of its business. The bank must submit a plan to SAMA to bring all material exposures for that category of transactions under the internal models method.
7.3. For all OTC derivative transactions and for all long settlement transactions for which a bank has not received approval from SAMA to use the internal models method, the bank must use the standardized approach to counterparty credit risk (SA-CCR, in Chapter 6 of this framework).
7.4. Exposures or EAD arising from long settlement transactions can be determined using either of the methods identified in this framework regardless of the methods chosen for treating OTC derivatives and SFTs. In computing capital requirements for long settlement transactions banks that hold permission to use the internal ratings-based approach may opt to apply the risk weights under this Framework’s standardized approach for credit risk on a permanent basis and irrespective to the materiality of such positions.
7.5. After adoption of the internal models method, the bank must comply with the above requirements on a permanent basis. Only under exceptional circumstances or for immaterial exposures can a bank revert to the standardized approach for counterparty credit risk for all or part of its exposure. The bank must demonstrate that reversion to a less sophisticated method does not lead to an arbitrage of the regulatory capital rules.
Exposure Amount or EAD Under the Internal Models Method
7.6. CCR exposure or EAD is measured at the level of the netting set as defined in Chapter 4 of this framework and 7.61 to 7.71 of this framework. A qualifying internal model for measuring counterparty credit exposure must specify the forecasting distribution for changes in the market value of the netting set attributable to changes in market variables, such as interest rates, foreign exchange rates, etc. The model then computes the bank’s CCR exposure for the netting set at each future date given the changes in the market variables. For margined counterparties, the model may also capture future collateral movements. Banks may include eligible financial collateral as defined in 9.37 of the Minimum Capital Requirements for Credit Risk and 9.2 of this framework in their forecasting distributions for changes in the market value of the netting set, if the quantitative, qualitative and data requirements for internal models method are met for the collateral.
7.7. Banks that use the internal models method must calculate credit RWA as the higher of two amounts, one based on current parameter estimates and one based on stressed parameter estimates. Specifically, to determine the default risk capital requirement for counterparty credit risk, banks must use the greater of the portfolio-level capital requirement (not including the credit valuation adjustment, or CVA, charge in Chapter 11 of this Framework) based on Effective expected positive exposure (EPE) using current market data and the portfolio level capital requirement based on Effective EPE using a stress calibration.24 The stress calibration should be a single consistent stress calibration for the whole portfolio of counterparties. The greater of Effective EPE using current market data and the stress calibration should not be applied on a counterparty by counterparty basis, but on a total portfolio level.
7.8. To the extent that a bank recognizes collateral in EAD via current exposure, a bank would not be permitted to recognize the benefits in its estimates of loss given-default (LGD). As a result, the bank would be required to use an LGD of an otherwise similar uncollateralized facility. In other words, the bank would be required to use an LGD that does not include collateral that is already included in EAD.
7.9. Under the internal models method, the bank need not employ a single model. Although the following text describes an internal model as a simulation model, no particular form of model is required. Analytical models are acceptable so long as they are subject to supervisory review, meet all of the requirements set forth in this section and are applied to all material exposures subject to a CCR-related capital requirement as noted above, with the exception of long settlement transactions, which are treated separately, and with the exception of those exposures that are immaterial in size and risk.
7.10. Expected exposure or peak exposure measures should be calculated based on a distribution of exposures that accounts for the possible non-normality of the distribution of exposures, including the existence of leptokurtosis (“fat tails”), where appropriate.
7.11. When using an internal model, exposure amount or EAD is calculated as the product of alpha times Effective EPE, as specified below (except for counterparties that have been identified as having explicit specific wrong way risk – see 7.48):
EAD = α × EffectiveEPE (Equation 1)
7.12. Effective EPE is computed by estimating expected exposure (EEt) as the average t exposure at future date t, where the average is taken across possible future values of relevant market risk factors, such as interest rates, foreign exchange rates, etc. The internal model estimates EE at a series of future dates t1, t2, t3 ...25 Specifically, “Effective EE” is computed recursively using the following formula, where the current date is denoted as t0 and Effective EEt0 equals current exposure:
EffectiveEEtk = max(EffectiveEEtk-1, EEtk (Equation 2)
7.13. In this regard, “Effective EPE” is the average Effective EE during the first year of future exposure. If all contracts in the netting set mature before one year, EPE is the average of expected exposure until all contracts in the netting set mature. Effective EPE is computed as a weighted average of Effective EE, using the following formula where the weights Δtk= tk - tk-1 allows for the case when future exposure is calculated at dates that are not equally spaced over time:

7.14. Alpha (α) is set equal to 1.4.
7.15. SAMA may require a higher alpha based on a bank’s CCR exposures. Factors that may require a higher alpha include the low granularity of counterparties; particularly high exposures to general wrong-way risk; particularly high correlation of market values across counterparties; and other institution specific characteristics of CCR exposures.
Own estimates for alpha
7.16. Banks should seek approval from SAMA to compute internal estimates of alpha subject to a floor of 1.2, where alpha equals the ratio of economic capital from a full simulation of counterparty exposure across counterparties (numerator) and economic capital based on EPE (denominator), assuming they meet certain operating requirements. Eligible banks must meet all the operating requirements for internal estimates of EPE and must demonstrate that their internal estimates of alpha capture in the numerator the material sources of stochastic dependency of distributions of market values of transactions or of portfolios of transactions across counterparties (e.g. the correlation of defaults across counterparties and between market risk and default).
7.17. In the denominator, EPE must be used as if it were a fixed outstanding loan amount.
7.18. To this end, banks must ensure that the numerator and denominator of alpha are computed in a consistent fashion with respect to the modelling methodology, parameter specifications and portfolio composition. The approach used must be based on the bank's internal economic capital approach, be well-documented and be subject to independent validation. In addition, banks must review their estimates on at least a quarterly basis, and more frequently when the composition of the portfolio varies over time. Banks must assess the model risk and inform SAMA of any significant variation in estimates of alpha that arises from the possibility for mis-specification in the models used for the numerator, especially where convexity is present.
7.19. Where appropriate, volatilities and correlations of market risk factors used in the joint simulation of market and credit risk should be conditioned on the credit risk factor to reflect potential increases in volatility or correlation in an economic downturn. Internal estimates of alpha should take account of the granularity of exposures.
24 Effective expected positive exposure (EPE) using current market data to be compared with Effective EPE using a stress calibration on annual basis during ICAAP
25 In theory, the expectations should be taken with respect to the actual probability distribution of future exposure and not the risk-neutral one. Supervisors recognize that practical considerations may make it more feasible to use the risk-neutral one. As a result, supervisors will not mandate which kind of forecasting distribution to employ.Maturity
7.20. If the original maturity of the longest-dated contract contained in the set is greater than one year, the formula for effective maturity (M) in 12.42 of the Minimum Capital Requirements for Credit Risk is replaced with formula that follows, where dfK is the risk-free discount factor for future time period tK and the remaining symbols are defined above. Similar to the treatment under corporate exposures, M has a cap of five years.26
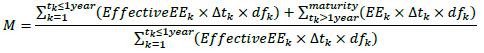
7.21. For netting sets in which all contracts have an original maturity of less than one year, the formula for effective maturity (M) i in 12.42 of the Minimum Capital Requirements for Credit Risk is unchanged and a floor of one year applies, with the exception of short-term exposures as described in paragraphs in 12.45 to 12.48 of the Minimum Capital Requirements for Credit Risk.
26 Conceptually, M equals the effective credit duration of the counterparty exposure. A bank that uses an internal model to calculate a one-sided credit valuation adjustment (CVA) can use the effective credit duration estimated by such a model in place of the above formula with prior approval of SAMA.
Margin Agreements
7.22. If the netting set is subject to a margin agreement and the internal model captures the effects of margining when estimating EE, the model's EE measure may be used directly in (Equation 2) in 7.12. Such models are noticeably more complicated than models of EPE for unmargined counterparties.
7.23. An EPE model must also include transaction-specific information in order to capture the effects of margining. It must take into account both the current amount of margin and margin that would be passed between counterparties in the future. Such a model must account for the nature of margin agreements (unilateral or bilateral), the frequency of margin calls, the margin period of risk, the thresholds of unmargined exposure the bank is willing to accept, and the minimum transfer amount. Such a model must either model the mark-to-market change in the value of collateral posted or apply this Framework's rules for collateral.
7.24. For transactions subject to daily re-margining and mark-to-market valuation, a supervisory floor of five business days for netting sets consisting only of repo style transactions, and 10 business days for all other netting sets is imposed on the margin period of risk used for the purpose of modelling EAD with margin agreements. In the following cases a higher supervisory floor is imposed:
(1) For all netting sets where the number of trades exceeds 5000 at any point during a quarter, a supervisory floor of 20 business days is imposed for the margin period of risk for the following quarter.
(2) For netting sets containing one or more trades involving either illiquid collateral, or an OTC derivative that cannot be easily replaced, a supervisory floor of 20 business days is imposed for the margin period of risk. For these purposes, "Illiquid collateral" and "OTC derivatives that cannot be easily replaced" must be determined in the context of stressed market conditions and will be characterized by the absence of continuously active markets where a counterparty would, within two or fewer days, obtain multiple price quotations that would not move the market or represent a price reflecting a market discount (in the case of collateral) or premium (in the case of an OTC derivative). Examples of situations where trades are deemed illiquid for this purpose include, but are not limited to, trades that are not marked daily and trades that are subject to specific accounting treatment for valuation purposes (e.g. OTC derivatives or repo-style transactions referencing securities whose fair value is determined by models with inputs that are not observed in the market).
(3) In addition, a bank must consider whether trades or securities it holds as collateral are concentrated in a particular counterparty and if that counterparty exited the market precipitously whether the bank would be able to replace its trades.
7.25. If a bank has experienced more than two margin call disputes on a particular netting set over the previous two quarters that have lasted longer than the applicable margin period of risk (before consideration of this provision), then the bank must reflect this history appropriately by using a margin period of risk that is at least double the supervisory floor for that netting set for the subsequent two quarters.
7.26. For re-margining with a periodicity of N-days the margin period of risk should be at least equal to the supervisory floor, F, plus the N days minus one day. That is:
Margin Period of Risk = F + N — 1
7.27. Banks using the internal models method must not capture the effect of a reduction of EAD due to any clause in a collateral agreement that requires receipt of collateral when counterparty credit quality deteriorates.
Model validation
7.28. The extent to which banks meet the qualitative criteria may influence the level at which SAMA will set the multiplication factor referred to in 7.14 (Alpha) above. Only those banks in full compliance with the qualitative criteria will be eligible for application of the minimum multiplication factor. The qualitative criteria include:
(1) The bank must conduct a regular program of backtesting, i.e. an ex-post comparison of the risk measures generated by the model against realized risk measures, as well as comparing hypothetical changes based on static positions with realized measures. “Risk measures” in this context, refers not only to Effective EPE, the risk measure used to derive regulatory capital, but also to the other risk measures used in the calculation of Effective EPE such as the exposure distribution at a series of future dates, the positive exposure distribution at a series of future dates, the market risk factors used to derive those exposures and the values of the constituent trades of a portfolio.
(2) The bank must carry out an initial validation and an on-going periodic review of its IMM model and the risk measures generated by it. The validation and review must be independent of the model developers.
(3) The board of directors and senior management should be actively involved in the risk control process and must regard credit and counterparty credit risk control as an essential aspect of the business to which significant resources need to be devoted. In this regard, the daily reports prepared by the independent risk control unit must be reviewed by a level of management with sufficient seniority and authority to enforce both reductions of positions taken by individual traders and reductions in the bank’s overall risk exposure.
(4) The bank’s internal risk measurement exposure model must be closely integrated into the day-to-day risk management process of the bank. Its output should accordingly be an integral part of the process of planning, monitoring and controlling the bank’s counterparty credit risk profile.
(5) The risk measurement system should be used in conjunction with internal trading and exposure limits. In this regard, exposure limits should be related to the bank’s risk measurement model in a manner that is consistent over time and that is well understood by traders, the credit function and senior management.
(6) Banks should have a routine in place for ensuring compliance with a documented set of internal policies, controls and procedures concerning the operation of the risk measurement system. The bank’s risk measurement system must be well documented, for example, through a risk management manual that describes the basic principles of the risk management system and that provides an explanation of the empirical techniques used to measure counterparty credit risk.
(7) An independent review of the risk measurement system should be carried out regularly in the bank’s own internal auditing process. This review should include both the activities of the business trading units and of the independent risk control unit. A review of the overall risk management process should take place at regular intervals (ideally no less than once a year) and should specifically address, at a minimum:
(a) The adequacy of the documentation of the risk management system and process;
(b) The organization of the risk control unit;
(c) The integration of counterparty credit risk measures into daily risk management;
(d) The approval process for counterparty credit risk models used in the calculation of counterparty credit risk used by front office and back office personnel;
(e) The validation of any significant change in the risk measurement process;
(f) The scope of counterparty credit risks captured by the risk measurement model;
(g) The integrity of the management information system;
(h) The accuracy and completeness of position data;
(i) The verification of the consistency, timeliness and reliability of data sources used to run internal models, including the independence of such data sources;
(j) The accuracy and appropriateness of volatility and correlation assumptions;
(k) The accuracy of valuation and risk transformation calculations; and
(l) The verification of the model’s accuracy as described below in 7.29 to 7.33.
(8) The on-going validation of counterparty credit risk models, including backtesting, must be reviewed periodically by a level of management with sufficient authority to decide the course of action that will be taken to address weaknesses in the models.
7.29. Banks must document the process for initial and on-going validation of their IMM model to a level of detail that would enable a third party to recreate the analysis. Banks must also document the calculation of the risk measures generated by the models to a level of detail that would allow a third party to recreate the risk measures. This documentation must set out the frequency with which backtesting analysis and any other on-going validation will be conducted, how the validation is conducted with respect to dataflows and portfolios and the analyses that are used.
7.30. Banks must define criteria with which to assess their EPE models and the models that input into the calculation of EPE and have a written policy in place that describes the process by which unacceptable performance will be determined and remedied.
7.31. Banks must define how representative counterparty portfolios are constructed for the purposes of validating an EPE model and its risk measures.
7.32. When validating EPE models and its risk measures that produce forecast distributions, validation must assess more than a single statistic of the model distribution.
7.33. As part of the initial and on-going validation of an IMM model and its risk measures, the following requirements must be met:
(1) A bank must carry out backtesting using historical data on movements in market risk factors prior to SAMA approval. Backtesting must consider a number of distinct prediction time horizons out to at least one year, over a range of various start (initialization) dates and covering a wide range of market conditions.
(2) Banks must backtest the performance of their EPE model and the model’s relevant risk measures as well as the market risk factor predictions that support EPE. For collateralized trades, the prediction time horizons considered must include those reflecting typical margin periods of risk applied in collateralized/margined trading, and must include long time horizons of at least 1 year.
(3) The pricing models used to calculate counterparty credit risk exposure for a given scenario of future shocks to market risk factors must be tested as part of the initial and on-going model validation process. These pricing models may be different from those used to calculate Market Risk over a short horizon. Pricing models for options must account for the nonlinearity of option value with respect to market risk factors.
(4) An EPE model must capture transaction specific information in order to aggregate exposures at the level of the netting set. Banks must verify that transactions are assigned to the appropriate netting set within the model.
(5) Static, historical backtesting on representative counterparty portfolios must be a part of the validation process. At regular intervals as directed by SAMA, a bank must conduct such backtesting on a number of representative counterparty portfolios. The representative portfolios must be chosen based on their sensitivity to the material risk factors and correlations to which the bank is exposed. In addition, IMM banks need to conduct backtesting that is designed to test the key assumptions of the EPE model and the relevant risk measures, e.g. the modelled relationship between tenors of the same risk factor, and the modelled relationships between risk factors.
(6) Significant differences between realized exposures and the forecast distribution could indicate a problem with the model or the underlying data that SAMA would require the bank to correct. Under such circumstances, SAMA may require additional capital to be held while the problem is being solved.
(7) The performance of EPE models and its risk measures must be subject to good backtesting practice. The backtesting program must be capable of identifying poor performance in an EPE model’s risk measures.
(8) Banks must validate their EPE models and all relevant risk measures out to time horizons commensurate with the maturity of trades for which exposure is calculated using an internal models method.
(9) The pricing models used to calculate counterparty exposure must be regularly tested against appropriate independent benchmarks as part of the on-going model validation process.
(10) The on-going validation of a bank’s EPE model and the relevant risk measures include an assessment of recent performance.
(11) The frequency with which the parameters of an EPE model are updated needs to be assessed as part of the validation process.
(12) Under the IMM, a measure that is more conservative than the metric used to calculate regulatory EAD for every counterparty, may be used in place of alpha times Effective EPE with the prior approval of SAMA. The degree of relative conservatism will be assessed upon initial SAMA approval and at the regular supervisory reviews of the EPE models. The bank must validate the conservatism regularly.
(13) The on-going assessment of model performance needs to cover all counterparties for which the models are used.
(14) The validation of IMM models must assess whether or not the bank level and netting set exposure calculations of EPE are appropriate.
Operational requirements for EPE models
7.34. In order to be eligible to adopt an internal model for estimating EPE arising from CCR for regulatory capital purposes, a bank must meet the following operational requirements. These include meeting the requirements related to the qualifying standards on CCR Management, a use test, stress testing, identification of wrong way risk, and internal controls.
Qualifying standards on CCR Management
7.35. The bank must satisfy SAMA that, in addition to meeting the operational requirements identified in 7.36 to 7.60 below, it adheres to sound practices for CCR management, including those specified in Counterparty credit risks section of the Credit Risk chapter of the Supervisory Review Process in the Basel Framework.
Use test
7.36. The distribution of exposures generated by the internal model used to calculate effective EPE must be closely integrated into the day-to-day CCR management process of the bank. For example, the bank could use the peak exposure from the distributions for counterparty credit limits or expected positive exposure for its internal allocation of capital. The internal model’s output must accordingly play an essential role in the credit approval, counterparty credit risk management, internal capital allocations, and corporate governance of banks that seek approval to apply such models for capital adequacy purposes. Models and estimates designed and implemented exclusively to qualify for the internal models method (IMM) are not acceptable.
7.37. A bank must have a credible track record in the use of internal models that generate a distribution of exposures to CCR. Thus, the bank must demonstrate that it has been using an internal model to calculate the distributions of exposures upon which the EPE calculation is based that meets broadly the minimum requirements for at least one year prior to SAMA approval.
7.38. Banks employing the internal models method must have an independent control unit that is responsible for the design and implementation of the bank’s CCR management system, including the initial and on-going validation of the internal model. This unit must control input data integrity and produce and analyze daily reports on the output of the bank’s risk measurement model, including an evaluation of the relationship between measures of CCR risk exposure and credit and trading limits. This unit must be independent from business credit and trading units; it must be adequately staffed; it must report directly to senior management of the bank. The work of this unit should be closely integrated into the day-to-day credit risk management process of the bank. Its output should accordingly be an integral part of the process of planning, monitoring and controlling the bank’s credit and overall risk profile.
7.39. Banks applying the internal models method must have a collateral management unit that is responsible for calculating and making margin calls, managing margin call disputes and reporting levels of independent amounts, initial margins and variation margins accurately on a daily basis. This unit must control the integrity of the data used to make margin calls, and ensure that it is consistent and reconciled regularly with all relevant sources of data within the bank. This unit must also track the extent of reuse of collateral (both cash and non-cash) and the rights that the bank gives away to its respective counterparties for the collateral that it posts. These internal reports must indicate the categories of collateral assets that are reused, and the terms of such reuse including instrument, credit quality and maturity. The unit must also track concentration to individual collateral asset classes accepted by the banks. Senior management must allocate sufficient resources to this unit for its systems to have an appropriate level of operational performance, as measured by the timeliness and accuracy of outgoing calls and response time to incoming calls. Senior management must ensure that this unit is adequately staffed to process calls and disputes in a timely manner even under severe market crisis, and to enable the bank to limit its number of large disputes caused by trade volumes.
7.40. The bank's collateral management unit must produce and maintain appropriate collateral management information that is reported on a regular basis to senior management. Such internal reporting should include information on the type of collateral (both cash and non-cash) received and posted, as well as the size, aging and cause for margin call disputes. This internal reporting should also reflect trends in these figures.
7.41. A bank employing the internal models method must ensure that its cash management policies account simultaneously for the liquidity risks of potential incoming margin calls in the context of exchanges of variation margin or other margin types, such as initial or independent margin, under adverse market shocks, potential incoming calls for the return of excess collateral posted by counterparties, and calls resulting from a potential downgrade of its own public rating. The bank must ensure that the nature and horizon of collateral reuse is consistent with its liquidity needs and does not jeopardize its ability to post or return collateral in a timely manner.
7.42. The internal model used to generate the distribution of exposures must be part of a counterparty risk management framework that includes the identification, measurement, management, approval and internal reporting of counterparty risk.27 This Framework must include the measurement of usage of credit lines (aggregating counterparty exposures with other credit exposures) and economic capital allocation. In addition to EPE (a measure of future exposure), a bank must measure and manage current exposures. Where appropriate, the bank must measure current exposure gross and net of collateral held. The use test is satisfied if a bank uses other counterparty risk measures, such as peak exposure or potential future exposure (PFE), based on the distribution of exposures generated by the same model to compute EPE.
7.43. A bank is not required to estimate or report EE daily, but to meet the use test it must have the systems capability to estimate EE daily, if necessary, unless it demonstrates to SAMA that its exposures to CCR warrant some less frequent calculation. It must choose a time profile of forecasting horizons that adequately reflects the time structure of future cash flows and maturity of the contracts. For example, a bank may compute EE on a daily basis for the first ten days, once a week out to one month, once a month out to eighteen months, once a quarter out to five years and beyond five years in a manner that is consistent with the materiality and composition of the exposure.
7.44. Exposure must be measured out to the life of all contracts in the netting set (not just to the one year horizon), monitored and controlled. The bank must have procedures in place to identify and control the risks for counterparties where exposure rises beyond the one-year horizon. Moreover, the forecasted increase in exposure must be an input into the bank’s internal economic capital model.
Stress testing
7.45. A bank must have in place sound stress testing processes for use in the assessment of capital adequacy. These stress measures must be compared against the measure of EPE and considered by the bank as part of its internal capital adequacy assessment process. Stress testing must also involve identifying possible events or future changes in economic conditions that could have unfavorable effects on a bank’s credit exposures and assessment of the bank’s ability to withstand such changes. Examples of scenarios that could be used are;
(i) economic or industry downturns,
(ii) market-place events, or
(iii) decreased liquidity conditions.
7.46. Banks must have a comprehensive stress testing program for counterparty credit risk. The stress testing program must include the following elements:
(1) Banks must ensure complete trade capture and exposure aggregation across all forms of counterparty credit risk (not just OTC derivatives) at the counterparty-specific level in a sufficient time frame to conduct regular stress testing.
(2) For all counterparties, banks should produce, at least monthly, exposure stress testing of principal market risk factors (e.g. interest rates, FX, equities, credit spreads, and commodity prices) in order to proactively identify, and when necessary, reduce outsized concentrations to specific directional sensitivities.
(3) Banks should apply multifactor stress testing scenarios and assess material non-directional risks (i.e. yield curve exposure, basis risks, etc.) at least quarterly. Multiple-factor stress tests should, at a minimum, aim to address scenarios in which a) severe economic or market events have occurred; b) broad market liquidity has decreased significantly; and c) the market impact of liquidating positions of a large financial intermediary. These stress tests may be part of bank-wide stress testing.
(4) Stressed market movements have an impact not only on counterparty exposures, but also on the credit quality of counterparties. At least quarterly, banks should conduct stress testing applying stressed conditions to the joint movement of exposures and counterparty creditworthiness.
(5) Exposure stress testing (including single factor, multifactor and material non-directional risks) and joint stressing of exposure and creditworthiness should be performed at the counterparty-specific, counterparty group (e.g. industry and region), and aggregate bank-wide CCR levels.
(6) Stress tests results should be integrated into regular reporting to senior management. The analysis should capture the largest counterparty-level impacts across the portfolio, material concentrations within segments of the portfolio (within the same industry or region), and relevant portfolio and counterparty specific trends.
(7) The severity of factor shocks should be consistent with the purpose of the stress test. When evaluating solvency under stress, factor shocks should be severe enough to capture historical extreme market environments and/or extreme but plausible stressed market conditions. The impact of such shocks on capital resources should be evaluated, as well as the impact on capital requirements and earnings. For the purpose of day-to-day portfolio monitoring, hedging, and management of concentrations, banks should also consider scenarios of lesser severity and higher probability.
(8) Banks should consider reverse stress tests to identify extreme, but plausible, scenarios that could result in significant adverse outcomes.
(9) Senior management must take a lead role in the integration of stress testing into the risk management framework and risk culture of the bank and ensure that the results are meaningful and proactively used to manage counterparty credit risk. At a minimum, the results of stress testing for significant exposures should be compared to guidelines that express the bank’s risk appetite and elevated for discussion and action when excessive or concentrated risks are present.
Wrong-way risk
7.47. Banks must identify exposures that give rise to a greater degree of general wrong-way risk. Stress testing and scenario analyses must be designed to identify risk factors that are positively correlated with counterparty credit worthiness. Such testing needs to address the possibility of severe shocks occurring when relationships between risk factors have changed. Banks should monitor general wrong way risk by product, by region, by industry, or by other categories that are germane to the business. Reports should be provided to senior management, the appropriate committee of the Board, or the delegated authority of the board on a regular basis that communicate wrong way risks and the steps that are being taken to manage that risk.
7.48. A bank is exposed to “specific wrong-way risk” if future exposure to a specific counterparty is highly correlated with the counterparty’s probability of default. For example, a company writing put options on its own stock creates wrong-way exposures for the buyer that is specific to the counterparty. A bank must have procedures in place to identify, monitor and control cases of specific wrong way risk, beginning at the inception of a trade and continuing through the life of the trade. To calculate the CCR capital requirement, the instruments for which there exists a legal connection between the counterparty and the underlying issuer, and for which specific wrong way risk has been identified, are not considered to be in the same netting set as other transactions with the counterparty. Furthermore, for single-name credit default swaps where there exists a legal connection between the counterparty and the underlying issuer, and where specific wrong way risk has been identified, EAD in respect of such swap counterparty exposure equals the full expected loss in the remaining fair value of the underlying instruments assuming the underlying issuer is in liquidation. The use of the full expected loss in remaining fair value of the underlying instrument allows the bank to recognize, in respect of such swap, the market value that has been lost already and any expected recoveries. Accordingly LGD for advanced or foundation IRB banks must be set to 100% for such swap transactions.28 For banks using the Standardized Approach, the risk weight to use is that of an unsecured transaction. For equity derivatives, bond options, securities financing transactions etc. referencing a single company where there exists a legal connection between the counterparty and the underlying company, and where specific wrong way risk has been identified, EAD equals the value of the transaction under the assumption of a jump-to-default of the underlying security. Inasmuch this makes re-use of possibly existing (market risk) calculations (for incremental risk charge) that already contain an LGD assumption, the LGD must be set to 100%.
Integrity of modelling process
7.49. Other operational requirements focus on the internal controls needed to ensure the integrity of model inputs; specifically, the requirements address the transaction data, historical market data, frequency of calculation, and valuation models used in measuring EPE.
7.50. The internal model must reflect transaction terms and specifications in a timely, complete, and conservative fashion. Such terms include, but are not limited to, contract notional amounts, maturity, reference assets, collateral thresholds, margining arrangements, netting arrangements, etc. The terms and specifications must reside in a secure database that is subject to formal and periodic audit. The process for recognizing netting arrangements must require signoff by legal staff to verify the legal enforceability of netting and be input into the database by an independent unit. The transmission of transaction terms and specifications data to the internal model must also be subject to internal audit and formal reconciliation processes must be in place between the internal model and source data systems to verify on an ongoing basis that transaction terms and specifications are being reflected in EPE correctly or at least conservatively.
7.51. When the Effective EPE model is calibrated using historic market data, the bank must employ current market data to compute current exposures and at least three years of historical data must be used to estimate parameters of the model. Alternatively, market implied data may be used to estimate parameters of the model. In all cases, the data must be updated quarterly or more frequently if market conditions warrant. To calculate the Effective EPE using a stress calibration, the bank must also calibrate Effective EPE using three years of data that include a period of stress to the credit default spreads of a bank’s counterparties or calibrate Effective EPE using market implied data from a suitable period of stress. The following process will be used to assess the adequacy of the stress calibration:
(1) The bank must demonstrate, at least quarterly, that the stress period coincides with a period of increased credit default swaps (CDS)or other credit spreads - such as loan or corporate bond spreads - for a representative selection of the bank’s counterparties with traded credit spreads. In situations where the bank does not have adequate credit spread data for a counterparty, the bank should map each counterparty to specific credit spread data based on region, internal rating and business types.
(2) The exposure model for all counterparties must use data, either historic or implied, that include the data from the stressed credit period, and must use such data in a manner consistent with the method used for the calibration of the Effective EPE model to current data.
(3) To evaluate the effectiveness of its stress calibration for Effective EPE, the bank must create several benchmark portfolios that are vulnerable to the same main risk factors to which the bank is exposed. The exposure to these benchmark portfolios shall be calculated using:
(a) current positions at current market prices, stressed volatilities, stressed correlations and other relevant stressed exposure model inputs from the 3-year stress period and
(b) current positions at end of stress period market prices, stressed volatilities, stressed correlations and other relevant stressed exposure model inputs from the 3-year stress period. SAMA may adjust the stress calibration if the exposures of these benchmark portfolios deviate substantially.
7.52. For a bank to recognize in its EAD calculations for OTC derivatives the effect of collateral other than cash of the same currency as the exposure itself, if it is not able to model collateral jointly with the exposure then it must use the standard supervisory haircuts of the comprehensive approach.
7.53. If the internal model includes the effect of collateral on changes in the market value of the netting set, the bank must model collateral other than cash of the same currency as the exposure itself jointly with the exposure in its EAD calculations for securities-financing transactions.
7.54. The EPE model (and modifications made to it) must be subject to an internal model validation process. The process must be clearly articulated in banks’ policies and procedures. The validation process must specify the kind of testing needed to ensure model integrity and identify conditions under which assumptions are violated and may result in an understatement of EPE. The validation process must include a review of the comprehensiveness of the EPE model, for example such as whether the EPE model covers all products that have a material contribution to counterparty risk exposures.
7.55. The use of an internal model to estimate EPE, and hence the exposure amount or EAD, of positions subject to a CCR capital requirement will be conditional upon the explicit approval of SAMA. SAMA and relevant supervisory authorities of banks that carry out material trading activities in multiple jurisdictions will work co-operatively to ensure an efficient approval process.
7.56. SAMA will require that banks seeking to make use of internal models to estimate EPE meet the requirements regarding, for example, the integrity of the risk management system, the skills of staff that will rely on such measures in operational areas and in control functions, the accuracy of models, and the rigour of internal controls over relevant internal processes. As an example, banks seeking to make use of an internal model to estimate EPE must demonstrate that they meet the general criteria for banks seeking to make use of internal models to assess market risk exposures, but in the context of assessing counterparty credit risk.29
7.57. The supervisory review process (SRP) standard of this framework provides general background and specific guidance to cover counterparty credit risks that may not be fully covered by the Pillar 1 process.
7.58. No particular form of model is required to qualify to make use of an internal model. Although this text describes an internal model as a simulation model, other forms of models, including analytic models, are acceptable subject to SAMA approval and review. Banks that seek recognition for the use of an internal model that is not based on simulations must demonstrate to SAMA that the model meets all operational requirements.
7.59. For a bank that qualifies to net transactions,
(1) The bank must have internal procedures to verify that, prior to including a transaction in a netting set,
(2) The transaction is covered by a legally enforceable netting contract that meets the applicable requirements of the standardized approach to counterparty credit risk (in Chapter 6 of this framework), chapter 9 of the Minimum Capital Requirements for Credit Risk, or the Cross Product Netting Rules set forth 7.61 to 7.71 below in this framework.
7.60. For a bank that makes use of collateral to mitigate its CCR, the bank must have internal procedures to verify that, prior to recognizing the effect of collateral in its calculations, the collateral meets the appropriate legal certainty standards as set out in chapter 9 of the Minimum Capital Requirements for Credit Risk.
Cross-product netting rules
7.61. The Cross-Product Netting Rules apply specifically to netting across SFTs, or to netting across both SFTs and OTC derivatives, for purposes of regulatory capital computation under IMM.
7.62. Banks that receive approval to estimate their exposures to CCR using the internal models method may include within a netting set SFTs, or both SFTs and OTC derivatives subject to a legally valid form of bilateral netting that satisfies the following legal and operational criteria for a Cross-Product Netting Arrangement (as defined below). The bank must also have satisfied any prior approval or other procedural requirements that SAMA determines to implement for purposes of recognizing a Cross-Product Netting Arrangement.
Legal Criteria
7.63. The bank has executed a written, bilateral netting agreement with the counterparty that creates a single legal obligation, covering all included bilateral master agreements and transactions (“Cross-Product Netting Arrangement”), such that the bank would have either a claim to receive or obligation to pay only the net sum of the positive and negative
(i) close-out values of any included individual master agreements and
(ii) mark-to-market values of any included individual transactions (the “Cross-Product Net Amount”), in the event a counterparty fails to perform due to any of the following: default, bankruptcy, liquidation or similar circumstances.
7.64. The bank has written and reasoned legal opinions that conclude with a high degree of certainty that, in the event of a legal challenge, relevant courts or administrative authorities would find the bank’s exposure under the Cross Product Netting Arrangement to be the Cross-Product Net Amount under the laws of all relevant jurisdictions. In reaching this conclusion, legal opinions must address the validity and enforceability of the entire Cross-Product Netting Arrangement under its terms and the impact of the Cross-Product Netting Arrangement on the material provisions of any included bilateral master agreement.
(1) The laws of “all relevant jurisdictions” are: (i) the law of the jurisdiction in which the counterparty is chartered and, if the foreign branch of a counterparty is involved, then also under the law of the jurisdiction in which the branch is located, (ii) the law that governs the individual transactions, and (iii) the law that governs any contract or agreement necessary to effect the netting.
(2) A legal opinion must be generally recognized as such by the legal community in the bank’s home country or a memorandum of law that addresses all relevant issues in a reasoned manner.
7.65. The bank has internal procedures to verify that, prior to including a transaction in a netting set, the transaction is covered by legal opinions that meet the above criteria.
7.66. The bank undertakes to update legal opinions as necessary to ensure continuing enforceability of the Cross-Product Netting Arrangement in light of possible changes in relevant law.
7.67. The Cross-Product Netting Arrangement does not include a walkaway clause. A walkaway clause is a provision which permits a non-defaulting counterparty to make only limited payments, or no payment at all, to the estate of the defaulter, even if the defaulter is a net creditor.
7.68. Each included bilateral master agreement and transaction included in the Cross Product Netting Arrangement satisfies applicable legal requirements for recognition of credit risk mitigation techniques in credit risk mitigation techniques in chapter 9 of the Minimum Capital Requirements for Credit Risk.
7.69. The bank maintains all required documentation in its files.
Operational Criteria
7.70. SAMA is satisfied that the effects of a Cross-Product Netting Arrangement are factored into the bank’s measurement of a counterparty’s aggregate credit risk exposure and that the bank manages its counterparty credit risk on such basis.
7.71. Credit risk to each counterparty is aggregated to arrive at a single legal exposure across products covered by the Cross-Product Netting Arrangement. This aggregation must be factored into credit limit and economic capital processes.
27 This section draws heavily on the Counterparty Risk Management Policy Group's paper, Improving Counterparty Risk Management Practices (June 1999).
28 Note that the recoveries may also be possible on the underlying instrument beneath such swap. The capital requirements for such underlying exposure are to be calculated without reduction for the swap which introduces wrong way risk. Generally this means that such underlying exposure will receive the risk weight and capital treatment associated with an unsecured transaction (i.e. assuming such underlying exposure is an unsecured credit exposure).
29 See Chapter 10.1 to Chapter 10.4 of the Minimum Capital Requirements for Market Risk.8. Capital Requirements for Bank Exposures to Central Counterparties
Scope of Application
8.1. This chapter applies to exposures to central counterparties arising from over-the counter (OTC) derivatives, exchange-traded derivatives transactions, securities financing transactions (SFTs) and long settlement transactions. Exposures arising from the settlement of cash transactions (equities, fixed income, spot foreign exchange and spot commodities) are not subject to this treatment.30 The settlement of cash transactions remains subject to the treatment described in chapter 25 of the Minimum Capital Requirements for Credit Risk.
8.2. When the clearing member-to-client leg of an exchange-traded derivatives transaction is conducted under a bilateral agreement, both the client bank and the clearing member are to capitalize that transaction as an OTC derivative.31 This treatment also applies to transactions between lower-level clients and higher level clients in a multi-level client structure.
30 For contributions to prepaid default funds covering settlement-risk only products, the applicable risk weight is 0%.
31 For this purpose, the treatment in 8.12 would also apply.Central Counterparties
8.3. Regardless of whether a central counterparty (CCP) is classified as a qualifying CCP (QCCP), a bank retains the responsibility to ensure that it maintains adequate capital for its exposures. Under Pillar 2, a bank should consider whether it might need to hold capital in excess of the minimum capital requirements if, for example:
(1) its dealings with a CCP give rise to more risky exposures;
(2) where, given the context of that bank’s dealings, it is unclear that the CCP meets the definition of a QCCP; or
(3) an external assessment such as an International Monetary Fund Financial Sector Assessment Program (FSAP) has found material shortcomings in the CCP or the regulation of CCPs, and the CCP and/or the CCP regulator have not since publicly addressed the issues identified.
8.4. Where the bank is acting as a clearing member, the bank should assess through appropriate scenario analysis and stress testing whether the level of capital held against exposures to a CCP adequately addresses the inherent risks of those transactions. This assessment will include potential future or contingent exposures resulting from future drawings on default fund commitments, and/or from secondary commitments to take over or replace offsetting transactions from clients of another clearing member in case of this clearing member defaulting or becoming insolvent.
8.5. A bank must monitor and report to senior management, the appropriate committee of the Board, or the delegated authority of the board on a regular basis all of its exposures to CCPs, including exposures arising from trading through a CCP and exposures arising from CCP membership obligations such as default fund contributions.
8.6. Where a bank is clearing derivative, SFT and/or long settlement transactions through a QCCP as defined in Chapter 3 of this framework, then paragraphs 8.7 to 8.40 will apply. In the case of non-qualifying CCPs, paragraphs 8.41 and 8.42 will apply. Within three months of a CCP ceasing to qualify as a QCCP, unless SAMA requires otherwise, the trades with a former QCCP may continue to be capitalized as though they are with a QCCP. After that time, the bank’s exposures with such a CCP must be capitalized according to paragraphs 8.41 and 8.42.
Exposures to Qualifying CCPs: Trade Exposures
Clearing member exposures to CCPs
8.7. Where a bank acts as a clearing member of a CCP for its own purposes, a risk weight of 2% must be applied to the bank’s trade exposure to the CCP in respect of OTC derivatives, exchange-traded derivative transactions, SFTs and long settlement transactions. Where the clearing member offers clearing services to clients, the 2% risk weight also applies to the clearing member’s trade exposure to the CCP that arises when the clearing member is obligated to reimburse the client for any losses suffered due to changes in the value of its transactions in the event that the CCP defaults. The risk weight applied to collateral posted to the CCP by the bank must be determined in accordance with paragraphs 8.18 to 8.23.
8.8. The exposure amount for a bank’s trade exposure is to be calculated in accordance with methods set out in the counterparty credit risk overview chapters of this framework (see paragraph 5.7), as consistently applied by the bank in the ordinary course of its business.32 In applying these methods:
(1) Provided that the netting set does not contain illiquid collateral or exotic trades and provided there are no disputed trades, the 20-day floor for the margin period of risk (MPOR) established for netting sets where the number of trades exceeds 5000 does not apply. This floor is set out in 6.54(1) of the standardized approach for counterparty credit risk (SA- CCR), 9.60 of the Minimum Capital Requirements for Credit Risk of comprehensive approach within the standardized approach to credit risk and 7.24(1) of the internal models method (IMM).
(2) In all cases, a minimum MPOR of 10 days must be used for the calculation of trade exposures to CCPs for OTC derivatives.
(3) Where CCPs retain variation margin against certain trades (e.g. where CCPs collect and hold variation margin against positions in exchange-traded or OTC forwards), and the member collateral is not protected against the insolvency of the CCP, the minimum time risk horizon applied to banks' trade exposures on those trades must be the lesser of one year and the remaining maturity of the transaction, with a floor of 10 business days.
8.9. The methods for calculating counterparty credit risk exposures (see 5.7), when applied to bilateral trading exposures (i.e. non-CCP counterparties), require banks to calculate exposures for each individual netting set. However, netting arrangements for CCPs are not as standardized as those for OTC netting agreements in the context of bilateral trading. As a consequence, paragraph 8.10 below makes certain adjustments to the methods for calculating counterparty credit risk exposure to permit netting under certain conditions for exposures to CCPs.
8.10 Where settlement is legally enforceable on a net basis in an event of default and regardless of whether the counterparty is insolvent or bankrupt, the total replacement cost of all contracts relevant to the trade exposure determination can be calculated as a net replacement cost if the applicable close-out netting sets meet the requirements set out in:
(1) 9.68 of the Minimum Capital Requirements for Credit Risk and, where applicable, also 9.69 of the Minimum Capital Requirements for Credit Risk.
(2) 6.9 and 6.10 of the SA-CCR in this framework in the case of derivative transactions.
(3) 7.61 to 7.71 of IMM in the case of cross-product netting.
8.11 To the extent that the rules referenced in 8.10 above include the term “master agreement” or the phrase “a netting contract with a counterparty or other agreement”, this terminology must be read as including any enforceable arrangement that provides legally enforceable rights of set-off. If the bank cannot demonstrate that netting agreements meet these requirements, each single transaction will be regarded as a netting set of its own for the calculation of trade exposure.
Clearing member exposures to clients
8.12 The clearing member will always capitalize its exposure (including potential credit valuation adjustment, or CVA, risk exposure) to clients as bilateral trades, irrespective of whether the clearing member guarantees the trade or acts as an intermediary between the client and the CCP. However, to recognize the shorter close-out period for cleared client transactions, clearing members can capitalize the exposure to their clients applying a margin period of risk of at least five days in IMM or SA-CCR. The reduced exposure at default (EAD) should also be used for the calculation of the CVA capital requirement.
8.13 If a clearing member collects collateral from a client for client cleared trades and this collateral is passed on to the CCP, the clearing member may recognize this collateral for both the CCP-clearing member leg and the clearing member-client leg of the client-cleared trade. Therefore, initial margin posted by clients to their clearing member mitigates the exposure the clearing member has against these clients. The same treatment applies, in an analogous fashion, to multi-level client structures (between a higher-level client and a lower-level client).
Client exposures
8.14 Subject to the two conditions set out in 8.15 below being met, the treatment set out in 8.7 to 8.11 (i.e. the treatment of clearing member exposures to CCPs) also applies to the following:
(1) A bank's exposure to a clearing member where:
(a) the bank is a client of the clearing member; and
(b) the transactions arise as a result of the clearing member acting as a financial intermediary (i.e. the clearing member completes an offsetting transaction with a CCP).
(2) A bank's exposure to a CCP resulting from a transaction with the CCP where:
(a) the bank is a client of a clearing member; and
(b) the clearing member guarantees the performance the bank's exposure to the CCP.
(3) Exposures of lower-level clients to higher-level clients in a multi-level client structure, provided that for all client levels in-between the two conditions in 8.15 below are met.
8.15 The two conditions referenced in 8.14 above are:
(1) The offsetting transactions are identified by the CCP as client transactions and collateral to support them is held by the CCP and/or the clearing member, as applicable, under arrangements that prevent any losses to the client due to: (a) the default or insolvency of the clearing member; (b) the default or insolvency of the clearing member's other clients; and (c) the joint default or insolvency of the clearing member and any of its other clients. Regarding the condition set out in this paragraph:
(a) Upon the insolvency of the clearing member, there must be no legal impediment (other than the need to obtain a court order to which the client is entitled) to the transfer of the collateral belonging to clients of a defaulting clearing member to the CCP, to one or more other surviving clearing members or to the client or the client's nominee. SAMA should be consulted to determine whether this is achieved based on particular facts and SAMA will consult and communicate with other supervisors.
(b) The client must have conducted a sufficient legal review (and undertake such further review as necessary to ensure continuing enforceability) and have a well founded basis to conclude that, in the event of legal challenge, the relevant courts and administrative authorities would find that such arrangements mentioned above would be legal, valid, binding and enforceable under the relevant laws of the relevant jurisdiction(s).
(2) Relevant laws, regulation, rules, contractual, or administrative arrangements provide that the offsetting transactions with the defaulted or insolvent clearing member are highly likely to continue to be indirectly transacted through the CCP, or by the CCP, if the clearing member defaults or becomes insolvent. In such circumstances, the client positions and collateral with the CCP will be transferred at market value unless the client requests to close out the position at market value. Regarding the condition set out in this paragraph, if there is a clear precedent for transactions being ported at a CCP and industry intent for this practice to continue, then these factors must be considered when assessing if trades are highly likely to be ported. The fact that CCP documentation does not prohibit client trades from being ported is not sufficient to say they are highly likely to be ported.
8.16 Where a client is not protected from losses in the case that the clearing member and another client of the clearing member jointly default or become jointly insolvent, but all other conditions in the preceding paragraph are met, a risk weight of 4% will apply to the client's exposure to the clearing member, or to the higher-level client, respectively.
8.17 Where the bank is a client of the clearing member and the requirements in 8.14 to 8.16 above are not met, the bank will capitalize its exposure (including potential CVA risk exposure) to the clearing member as a bilateral trade.
Treatment of posted collateral
8.18 In all cases, any assets or collateral posted must, from the perspective of the bank posting such collateral, receive the risk weights that otherwise applies to such assets or collateral under the capital adequacy framework, regardless of the fact that such assets have been posted as collateral. That is, collateral posted must receive the banking book or trading book treatment it would receive if it had not been posted to the CCP.
8.19 In addition to the requirements of 8.18 above, the posted assets or collateral are subject to the counterparty credit risk requirements, regardless of whether they are in the banking or trading book. This includes the increase in the counterparty credit risk exposure due to the application of haircuts. The counterparty credit risk requirements arise where assets or collateral of a clearing member or client are posted with a CCP or a clearing member and are not held in a bankruptcy remote manner. In such cases, the bank posting such assets or collateral must recognize credit risk based upon the assets or collateral being exposed to risk of loss based on the creditworthiness of the entity holding such assets or collateral, as described further below.
8.20 Where such collateral is included in the definition of trade exposures (see Chapter 3of this framework) and the entity holding the collateral is the CCP, the following risk weights apply where the assets or collateral is not held on a bankruptcy- remote basis:
(1) For banks that are clearing members a risk weight of 2% applies.
(2) For banks that are clients of clearing members:
(a) a 2% risk weight applies if the conditions established in 8.14 and 8.15 are met; or
(b) a 4% risk weight applies if the conditions in 8.16 are met.
8.21 Where such collateral is included in the definition of trade exposures (see Chapter 3 of this framework), there is no capital requirement for counterparty credit risk exposure (i.e. the related risk weight or EAD is equal to zero) if the collateral is: (a) held by a custodian; and (b) bankruptcy remote from the CCP. Regarding this paragraph:
(1) All forms of collateral are included, such as: cash, securities, other pledged assets, and excess initial or variation margin, also called overcollateralization.
(2) The word “custodian” may include a trustee, agent, pledgee, secured creditor or any other person that holds property in a way that does not give such person a beneficial interest in such property and will not result in such property being subject to legally-enforceable claims by such persons creditors, or to a court- ordered stay of the return of such property, if such person becomes insolvent or bankrupt.
8.22 The relevant risk weight of the CCP will apply to assets or collateral posted by a bank that do not meet the definition of trade exposures (for example treating the exposure as a financial institution under standardized approach or internal ratings-based approach to credit risk).
8.23 Regarding the calculation of the exposure, or EAD, where banks use the SA-CCR to calculate exposures, collateral posted which is not held in a bankruptcy remote manner must be accounted for in the net independent collateral amount term in accordance with 6.17 to 6.21. For banks using IMM models, the alpha multiplier must be applied to the exposure on posted collateral.
Default fund exposures
8.24 Where a default fund is shared between products or types of business with settlement risk only (e.g. equities and bonds) and products or types of business which give rise to counterparty credit risk i.e. OTC derivatives, exchange-traded derivatives, SFTs or long settlement transactions, all of the default fund contributions will receive the risk weight determined according to the formula and methodology set forth below, without apportioning to different classes or types of business or products. However, where the default fund contributions from clearing members are segregated by product types and only accessible for specific product types, the capital requirements for those default fund exposures determined according to the formulae and methodology set forth below must be calculated for each specific product giving rise to counterparty credit risk. In case the CCP's prefunded own resources are shared among product types, the CCP will have to allocate those funds to each of the calculations, in proportion to the respective product specific EAD.
8.25 Whenever a bank is required to capitalize for exposures arising from default fund contributions to a QCCP, clearing member banks will apply the following approach.
8.26 Clearing member banks will apply a risk weight to their default fund contributions determined according to a risk sensitive formula that considers
(i) the size and quality of a qualifying CCP's financial resources,
(ii) the counterparty credit risk exposures of such CCP, and
(iii) the application of such financial resources via the CCP's loss-bearing waterfall, in the case of one or more clearing member defaults. The clearing member bank's risk sensitive capital requirement for its default fund contribution (KCMi) must be calculated using the formulae and methodology set forth below.
8.27 The clearing member bank's risk-sensitive capital requirement for its default fund contribution (KCMi) is calculated in two steps:
(1) Calculate the hypothetical capital requirement of the CCP due to its counterparty credit risk exposures to all of its clearing members and their clients.
(2) Calculate the capital requirement for the clearing member bank.
Hypothetical capital requirement of the CCP
8.28 The first step in calculating the clearing member bank's capital requirement for its default fund contribution (KCMi) is to calculate the hypothetical capital requirement of the CCP (KCMi) due to its counterparty credit risk exposures to all of its clearing members and their clients. KCCP is a hypothetical capital requirement for a CCP, calculated on a consistent basis for the sole purpose of determining the capitalization of clearing member default fund contributions; it does not represent the actual capital requirements for a CCP which may be determined by a CCP and its supervisor.
8.29 K is calculated using the following formula, where: CCP
(1) RW is a risk weight of 20%33
(2) capital ratio is 8%
(3) CM is the clearing member
(4) EAD is the exposure amount of the CCP to clearing member ‘i', relating to I the valuation at the end of the regulatory reporting date before the margin called on the final margin call of that day is exchanged. The exposure includes both:
(a) the clearing member's own transactions and client transactions guaranteed by the clearing member; and
(b) all values of collateral held by the CCP (including the clearing member's prefunded default fund contribution) against the transactions in (a).
(5) The sum is over all clearing member accounts.

8.30 Where clearing members provide client clearing services, and client transactions and collateral are held in separate (individual or omnibus) sub-accounts to the clearing member's proprietary business, each such client sub-account should enter the sum in 8.29 above separately, i.e. the member EAD in the formula above is then the sum of the client sub-account EADs and any house sub-account EAD. This will ensure that client collateral cannot be used to offset the CCP's exposures to clearing members' proprietary activity in the calculation of KCCP. If any of these sub-accounts contains both derivatives and SFTs, the EAD of that sub-account is the sum of the derivative EAD and the SFT EAD.
8.31 In the case that collateral is held against an account containing both SFTs and derivatives, the prefunded initial margin provided by the member or client must be allocated to the SFT and derivatives exposures in proportion to the respective product-specific EADs, calculated according to:
(1) Chapter 9.67 to 9.71 of the Minimum Capital Requirements for Credit Risk; and
(2) SA-CCR (see Chapter 6 of this framework) for derivatives, without including the effects of collateral.
8.32 If the default fund contributions of the member (DFi) are not split with regard to i client and house sub-accounts, they must be allocated per sub-account according to the respective fraction the initial margin of that sub-account has in relation to the total initial margin posted by or for the account of the clearing member.
8.33 For derivatives, EADi is calculated as the bilateral trade exposure the CCP has i against the clearing member using the SA-CCR. In applying the SA-CCR:
(1) A MPOR of 10 business days must be used to calculate the CCP's potential future exposure to its clearing members on derivatives transactions (the 20 day floor on the MPOR for netting sets with more than 5000 trades does not apply).
(2) All collateral held by a CCP to which that CCP has a legal claim in the event of the default of the member or client, including default fund contributions of that member (DFi), is used to offset the CCP's exposure to that member or i client, through inclusion in the PFE multiplier in accordance with 6.23 to 6.25.
8.34 For SFTs, EADi is equal to max(EBRMi- IMi- DFi;0), where:
(1) EBRMi denotes the exposure value to clearing member ‘i' before risk mitigation under 9.68 to 9.72 of the Minimum Capital Requirements for Credit Risk; where, for the purposes of this calculation, variation margin that has been exchanged (before the margin called on the final margin call of that day) enters into the mark-to-market value of the transactions.
(2) IMi; is the initial margin collateral posted by the clearing member with the CCP.
(3) DFi is the prefunded default fund contribution by the clearing member that will be applied upon such clearing member's default, either along with or immediately following such member's initial margin, to reduce the CCP loss.
8.35 As regards the calculation in this first step (i.e. 8.28 to 8.34):
(1) Any haircuts to be applied for SFTs must be the standard supervisory haircuts set out in 9.44 of the Minimum Capital Requirements for Credit Risk.
(2) The holding periods for SFT calculations in 9.60 to 9.63 of the Minimum Capital Requirements for Credit Risk.
(3) The netting sets that are applicable to regulated clearing members are the same as those referred to in 8.10 and 8.11. For all other clearing members, they need to follow the netting rules as laid out by the CCP based upon notification of each of its clearing members. SAMA may demand more granular netting sets than laid out by the CCP.
Capital requirement for each clearing member
8.36. The second step in calculating the clearing member bank's capital requirement for its default fund contribution (KCMi) is to apply the following formula,34 where:
(1) KCMi is the capital requirement on the default fund contribution of clearing member bank i
(2) DFCMPref is the total prefunded default fund contributions from clearing members
(3) DRCCP is the CCP's prefunded own resources (e.g. contributed capital, retained earnings, etc.), which are contributed to the default waterfall, where these are junior or pari passu to prefunded member contributions
(4) DFiprefis the prefunded default fund contributions provided by clearing member bank i
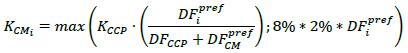
8.37. The CCP, bank, CCP supervisor or other body with access to the required data, must make a calculation of KCCP, DFCMpref, DFCCP, in such a way to permit the supervisor of the CCP to oversee those calculations, and it must share sufficient information of the calculation results to permit each clearing member to calculate their capital requirement for the default fund and for SAMA to review and confirm such calculations.
8.38. KCCP must be calculated on a quarterly basis at a minimum; although SAMA may require more frequent calculations in case of material changes (such as the CCP clearing a new product). The CCP, bank, CCP supervisor or other body that did the calculations must make available to SAMA the sufficient aggregate information about the composition of the CCP's exposures to clearing members and information provided to the clearing member for the purposes of the calculation of KCCP, DFCMpref, DFCCP. Such information must be provided no less frequently than the SAMA would require for monitoring the risk of the clearing member.
8.39. KCCP and KCMi must be recalculated at least quarterly, and should also be recalculated when there are material changes to the number or exposure of cleared transactions or material changes to the financial resources of the CCP.
Cap with regard to QCCPs
8.40. Where the sum of a bank's capital requirements for exposures to a QCCP due to its trade exposure and default fund contribution is higher than the total capital requirement that would be applied to those same exposures if the CCP were for a non-qualifying CCP, as outlined in 8.41 and 8.42 below, the latter total capital requirement shall be applied.
32 Where the firm’s internal model permission does not specifically cover centrally cleared products, the IMM scope would have to be extended to cover these products (even where the non-centrally cleared versions are included in the permission). Usually, national supervisors have a well-defined model approval/change process by which IMM firms can extend the products covered within their IMM scope. The introduction of a centrally cleared version of a product within the existing IMM scope must be considered as part of such a model change process, as opposed to a natural extension.
33 The 20% risk weight is a minimum requirement. As with other parts of the capital adequacy framework, the national supervisor of a bank may increase the risk weight. An increase in such risk weight would be appropriate if, for example, the clearing members in a CCP are not highly rated. Any such increase in risk weight is to be communicated by the affected banks to the person completing this calculation.
34 The formula puts a floor on the default fund exposure risk weight of 2%.Exposures to Non-Qualifying CCPs
8.41. Banks must apply the standardized approach for credit risk, according to the category of the counterparty, to their trade exposure to a non-qualifying CCP.
8.42. Banks must apply a risk weight of 1250% to their default fund contributions to a non-qualifying CCP. For the purposes of this paragraph, the default fund contributions of such banks will include both the funded and the unfunded contributions which are liable to be paid if the CCP so requires. Where there is a liability for unfunded contributions (i.e. unlimited binding commitments), the risk weight shall also be 1250%. Banks may, however, seek SAMA's approval to apply a different risk weight for the unfunded contributions.
9. Counterparty Credit Risk in the Trading Book
9.1 Banks must calculate the counterparty credit risk charge for over-the-counter (OTC) derivatives, repo-style and other transactions booked in the trading book, separate from the capital requirement for market risk.35 The risk weights to be used in this calculation must be consistent with those used for calculating the capital requirements in the banking book. Thus, banks using the standardized approach in the banking book will use the standardized approach risk weights in the trading book and banks using the internal ratings-based (IRB) approach in the banking book will use the IRB risk weights in the trading book in a manner consistent with the IRB roll-out situation in the banking book as described in 10.44 to 10.50 of the Minimum Capital Requirements for Credit Risk. For counterparties included in portfolios where the IRB approach is being used the IRB risk weights will have to be applied.
9.2 In the trading book, for repo-style transactions, all instruments, which are included in the trading book, may be used as eligible collateral. Those instruments which fall outside the banking book definition of eligible collateral shall be subject to a haircut at the level applicable to non-main index equities listed on recognized exchanges (as noted in 9.44 of the Minimum Capital Requirements for Credit Risk). Where banks are using a value-at-risk approach to measuring exposure for securities financing transactions, they also may apply this approach in the trading book in accordance with h 9.48 to 9.49 of the Minimum Capital Requirements for Credit Risk and Chapter 5 of this framework.
9.3 The calculation of the counterparty credit risk charge for collateralized OTC derivative transactions is the same as the rules prescribed for such transactions booked in the banking book (see Chapter 5 of this framework).
9.4 The calculation of the counterparty charge for repo-style transactions will be conducted using the rules in Chapter 5 of this framework spelt out for such transactions booked in the banking book. The firm-size adjustment for small or medium-sized entities as set out in chapter 11.9 of the Minimum Capital requirements for Credit Risk shall also be applicable in the trading book.
35 The treatment for unsettled foreign exchange and securities trades is set forth in the Risk weight multiplier to certain exposures with currency mismatch of the individual exposures under standardized approach for credit risk of Basel III: Finalizing post-crisis reforms.
10. Minimum Haircut Floors for Securities Financing Transactions
Scope
10.1 This chapter specifies the treatment of certain non-centrally cleared securities financing transactions (SFTs) with certain counterparties. The requirements are not applicable to banks in jurisdictions that are prohibited from conducting such transactions below the minimum haircut floors specified in 10.6 below.
10.2 The haircut floors found in 10.6 below apply to the following transactions:
(1) Non-centrally cleared SFTs in which the financing (i.e. the lending of cash) against collateral other than government securities is provided to counterparties who are not supervised by a regulator that imposes prudential requirements consistent with international norms.
(2) Collateral upgrade transactions with these same counterparties. A collateral upgrade transaction is when a bank lends a security to its counterparty and the counterparty pledges a lower-quality security as collateral, thus allowing the counterparty to exchange a lower-quality security for a higher quality security. For these transactions, the floors must be calculated according to the formula set out in 10.9 below.
10.3 SFTs with central banks are not subject to the haircut floors.
10.4 Cash-collateralized securities lending transactions are exempted from the haircut floors where:
(1) Securities are lent (to the bank) at long maturities and the lender of securities reinvests or employs the cash at the same or shorter maturity, therefore not giving rise to material maturity or liquidity mismatch.
(2) Securities are lent (to the bank) at call or at short maturities, giving rise to liquidity risk, only if the lender of the securities reinvests the cash collateral into a reinvestment fund or account subject to regulations or regulatory guidance meeting the minimum standards for reinvestment of cash collateral by securities lenders set out in Section 3.1 of the Policy Framework for Addressing Shadow Banking Risks in Securities Lending and Repos.36 For this purpose, banks may rely on representations by securities lenders that their reinvestment of cash collateral meets the minimum standards.
10.5 Banks that borrow (or lend) securities are exempted from the haircut floors on collateral upgrade transactions if the recipient of the securities that the bank has delivered as collateral (or lent) is either: (i) unable to re-use the securities (for example, because the securities have been provided under a pledge arrangement); or (ii) provides representations to the bank that they do not and will not re-use the securities.
36 Financial Stability Board, Strengthening oversight and regulation of shadow banking, Policy Framework for addressing shadow banking risks in securities lending and repos, 29 August 2013, fsb.org/wpcontent/uploads/r_130829b.
Haircut Floors
10.6 These are the haircut floors for SFTs referred to above (herein referred to as “in-scope SFTs”), expressed as percentages:
Residual maturity of collateral Haircut Level Corporate and other issuers Securitized products ≤ 1 year debt securities, and floating rate notes 0.5% 1% >1year, ≤ 5 years debt securities 1.5% 4% >5years, ≤ 10 years debt securities 3% 6% >10 years debt securities 4% 7% Main index equities 6% Other assets within the scope of the framework 10% 10.7. In-scope SFTs which do not meet the haircut floors must be treated as unsecured loans to the counterparties.
10.8. To determine whether the treatment in 10.7 applies to an in-scope SFT (or a netting set of SFTs in the case of portfolio-level haircuts), we must compare the collateral haircut H (real or calculated as per the rules below) and a haircut floor f (from 10.6 above or calculated as per the below rules).
Single in-scope SFTs
10.9. For a single in-scope SFT not included in a netting set, the values of H and f are computed as:
(1) For a single cash-lent-for-collateral SFT, H and f are known since H is simply defined by the amount of collateral received and f is given in 10.6.37 For the purposes of this calculation, collateral that is called by either counterparty can be treated collateral received from the moment that it is called (i.e. the treatment is independent of the settlement period).
(2) For a single collateral-for-collateral SFT, lending collateral A and receiving collateral B, the H is still be defined by the amount of collateral received but the effective floor of the transaction must integrate the floor of the two types of collateral and can be computed using the following formula, which will be compared to the effective haircut of the transaction, i.e. (CB/CA)-1.38
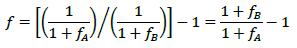
Netting set of SFTs
10.10. For a netting set of SFTs an effective "portfolio" floor of the transaction must be computed using the following formula,39 where:
(1) ES is the net position in each security (or cash) s that is net lent;
(2) Ct the net position that is net borrowed; and
(3) fs and ft are the haircut floors for the securities that are net lent and net s t borrowed respectively.
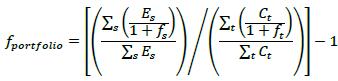
10.11. For a netting of SFTs, the portfolio does not breach the floor where:
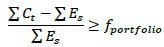
10.12. If the portfolio haircut does breach the floor, then the netting set of SFTs is subject to the treatment in 10.7. This treatment should be applied to all trades for which the security received appears in the table in 10.6 and for which, within the netting set, the bank is also a net receiver in that security. For the purposes of this calculation, collateral that is called by either counterparty can be treated collateral received from the moment that it is called (i.e. the treatment is independent of the settlement period).
10.13. The following portfolio of trades gives an example of how this methodology works (it shows a portfolio that does not breach the floor):
Actual trades Cash Sovereign debt Collateral A Collateral B Floor (fs) 0% 0% 6% 10% Portfolio of trades 50 100 -400 250 Es 50 100 0 250 Ct 0 0 400 0 fportfolio -0.00023 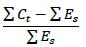
0 Minimum Capital Requirements for Credit Valuation Adjustment (CVA)
37 For example, consider an in-scope SFT where 100 cash is lent against 101 of a corporate debt security with a 12-year maturity, H is 1% [(101- 100)/100] and f is 4% (per 10.6). Therefore, the SFT in question would be subject to the treatment in 10.7.
38 For example, consider an in-scope SFT where 102 of a corporate debt security with a 10-year maturity is exchanged against 104 of equity, the effective haircut H of the transaction is 104/102 - 1 = 1.96% which has to be compared with the effective floor f of 1.06/1.03 - 1 =2.91%. Therefore, the SFT in question would be subject to the treatment in 10.7.
39 The formula calculates a weighted average floor of the portfolio.11. Credit Valuation Adjustment (CVA) Framework
Credit Valuation Adjustment (CVA) Overview
11.1. The risk-weighted assets for Credit Value Adjustment risk are determined by multiplying the capital requirements calculated as set out in Chapter 11 of this Framework by 12.5.
11.2. In the context of this framework, CVA stands for Credit Valuation Adjustment specified at a counterparty level. CVA reflects the adjustment of default risk-free prices of derivatives and Securities Financing Transactions (SFTs) due to a potential default of the counterparty.
11.3. Unless explicitly specified otherwise, the term CVA in this framework means regulatory CVA. Regulatory CVA may differ from CVA used for accounting purposes as follows:
(1) regulatory CVA excludes the effect of the bank's own default; and
(2) several constraints reflecting best practice in accounting CVA are imposed on calculations of regulatory CVA.
11.4. CVA risk is defined as the risk of losses arising from changing CVA values in response to changes in counterparty credit spreads and market risk factors that drive prices of derivative transactions and SFTs.
11.5. The capital requirement for CVA risk must be calculated by all banks involved in covered transactions in both banking book and trading book. Covered transactions include:
(1) all derivatives except those transacted directly with a qualified central counterparty and except those transactions meeting the conditions of 8.14 to 8.16 of this framework; and.
(2) SFTs that are fair-valued by a bank for accounting purposes, if SAMA determines that the bank's CVA loss exposures arising from SFT transactions are material. In case the bank deems the exposures immaterial, the bank must justify its assessment to SAMA by providing relevant supporting documentation.
(3) SFTs that are fair-valued for accounting purposes and for which a bank records zero for CVA reserves for accounting purposes are included in the scope of covered transactions.
11.6. The CVA risk capital requirement is calculated for a bank's “CVA portfolio” on a standalone basis. The CVA portfolio includes CVA for a bank's entire portfolio of covered transactions and eligible CVA hedges.
11.7. Two approaches are available for calculating CVA capital: the standardized approach (SA-CVA) and the basic approach (BA-CVA). Banks must use the BA- CVA unless they receive approval from Saudi Central Bank (SAMA) to use the SA-CVA.40
11.8. Banks that have received approval of Saudi Central Bank (SAMA) to use the SA- CVA may carve out from the SA-CVA calculations any number of netting sets. CVA capital for all carved out netting sets must be calculated using the BA-CVA. When applying the carve-out, a legal netting set may also be split into two synthetic netting sets, one containing the carved-out transactions subject to the BA-CVA and the other subject to the SA-CVA, subject to one or both of the following conditions:
(1) the split is consistent with the treatment of the legal netting set used by the bank for calculating accounting CVA (e.g. where certain transactions are not processed by the front office/accounting exposure model); or
(2) SAMA approval to use the SA-CVA is limited and does not cover all transactions within a legal netting set.
11.9. For banks that are below the materiality threshold where aggregate notional amount of non-centrally cleared derivatives is less than or equal to 446 billion SAR may opt not to calculate its CVA capital requirements using the SA-CVA or BA-CVA and instead choose an alternative treatment.
(1) Subject to the above conditions and treatment,
a. Banks may choose to set its CVA capital equal to 100% of the bank's capital requirement for counterparty credit risk (CCR);
b. Banks CVA hedges will not be recognized; and
c. Banks must apply this treatment to the bank's entire portfolio instead of the BA-CVA or the SA-CVA.
(2) SAMA, however, may not allow banks to apply the above treatment if it determines that CVA risk resulting from the bank's derivative positions materially contributes to the bank's overall risk.
11.10. Eligibility criteria for CVA hedges are specified in11.17 to 11.19 for the BA-CVA and in 11.37 to 11.39 for the SA-CVA.
11.11. CVA hedging instruments can be external (i.e. with an external counterparty) or internal (i.e. with one of the bank's trading desks).
(1) All external CVA hedges (including both eligible and ineligible external CVA hedges) that are covered transactions must be included in the CVA calculation for the counterparty to the hedge.
(2) All eligible external CVA hedges must be excluded from a bank's market risk capital requirement calculations under Chapter 2 through Chapter 14 of the Minimum Capital Requirements for Market Risk.
(3) Ineligible external CVA hedges are treated as trading book instruments and are capitalized under Chapter 2 through Chapter 14 of the Minimum Capital Requirements for Market Risk.
(4) An internal CVA hedge involves two perfectly offsetting positions: one of the CVA desk and the opposite position of the trading desk.
a) If an internal CVA hedge is ineligible, both positions belong to the trading book where they cancel each other, so there is no impact on either CVA portfolio or the trading book.
b) If an internal CVA hedge is eligible, the CVA desk's position is part of the CVA portfolio where it is capitalized as set out in this chapter, while the trading desk's position is part of the trading book where it is capitalized as set out in Chapter 2 through Chapter 14 of the Minimum Capital Requirements for Market Risk.
(5) If an internal CVA hedge involves an instrument that is subject to curvature risk, default risk charge or the residual risk add-on under the standardized approach as set out in Chapter 6 to Chapter 9 of the Minimum Capital Requirements for Market Risk, it can be eligible only if the trading desk that is the CVA desk's internal counterparty executes a transaction with an external counterparty that exactly offsets the trading desk's position with the CVA desk.
11.12. Banks that use the BA-CVA or the SA-CVA for calculating CVA capital requirements may cap the maturity adjustment factor at 1 for all netting sets contributing to CVA capital when they calculate CCR capital requirements under the Internal Ratings Based (IRB) approach.
40 Note that this is in contrast to the application of the market risk approaches set out in Chapter 3 of the Minimum Capital Requirements for Market Risk, where banks do not need SAMA approval to use the standardized approach.
Basic Approach for Credit Valuation Adjustment Risk
11.13. The BA-CVA calculations may be performed either via the reduced version or the full version. A bank under the BA-CVA approach can choose whether to implement the full version or the reduced version at its discretion. However, all banks using the BA-CVA must calculate the reduced version of BA-CVA capital requirements as the reduced BA-CVA is also part of the full BA-CVA capital calculations as a conservative means to limit hedging recognition.
(1) The full version recognizes counterparty spread hedges and is intended for banks that hedge CVA risk.
(2) The reduced version eliminates the element of hedging recognition from the full version. The reduced version is designed to simplify BA-CVA implementation for less sophisticated banks that do not hedge CVA.
Reduced version of the BA-CVA (hedges are not recognized)
11.14. The capital requirement for CVA risk under the reduced version of the BA-CVA (DSBA-CVA × Kreduced, where the discount scalar DSBA-CVA = 0.65) is calculated as follows (where the summations are taken over all counterparties that are within scope of the CVA charge), where:
(1) SCVAC is the CVA capital requirement that counterparty c would receive if considered on a stand-alone basis (referred to as “stand-alone CVA capital” below). See 11.15 for its calculation;
(2) ρ= 50%. It is supervisory correlation parameter. Its square, ρ2 = 25% represents the correlation between credit spreads of any two counterparties.41 In the formula below, the effect of p is to recognize the fact that the CVA risk to which a bank is exposed is less than the sum of the CVA risk for each counterparty, given that the credit spreads of counterparties are typically not perfectly correlated; and
(3) The first term under the square root in the formula below aggregates the systematic components of CVA risk, and the second term under the square root aggregates the idiosyncratic components of CVA risk.
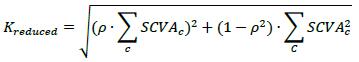
11.15. The stand-alone CVA capital requirements for counterparty c that are used in the formula in 11.14 (SCVAc) is calculated as follows (where the summation is across all netting sets with the counterparty), where:
(1) RWc is the risk weight for counterparty c that reflects the volatility of its credit spread. These risk weights are based on a combination of sector and credit quality of the counterparty as prescribed in 11.16.
(2) MNS is the effective maturity for the netting set NS. For banks that have SAMA’s approval to use IMM, NNS is calculated as per 7.20 and 7.21 of this framework, with the exception that the five year cap in 7.20 is not applied. For banks that do not have SAMA’s approval to use IMM, MNS is calculated according to chapter 12.46 to 12.54 of the Minimum Capital Requirements for Credit Risk, with the exception that the five-year cap in chapter 12.46 of the Minimum Capital Requirements for Credit Risk is not applied.
(3) EADNS is the exposure at default (EAD) of the netting set NS, calculated in the same way as the bank calculates it for minimum capital requirements for CCR.
(4) DFNS is a supervisory discount factor. It is 1 for banks using the IMM to calculate EAD, and is 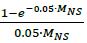 for banks not using IMM.42
for banks not using IMM.42
(5) ∝ = 1.4.43
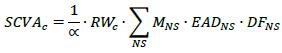
11.16. The supervisory risk weights (RWc) are given in Table 1. Credit quality is specified as either investment grade (IG), high yield (HY), or not rated (NR). Where there are no external ratings or where external ratings are not recognized within a jurisdiction, banks may, subject to SAMA's approval, map the internal rating to an external rating and assign a risk weight corresponding to either IG or HY. Otherwise, the risk weights corresponding to NR is to be applied.
Table 1: Supervisory risk weights, RWc Sector of counterparty Credit quality of counterparty IG HY and NR Sovereigns including central banks, multilateral development banks 0.5% 2.0% Local government, government-backed nonfinancials, education and public administration 1.0% 4.0% Financials including government-backed financials 5.0% 12.0% Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying 3.0% 7.0% Consumer goods and services, transportation and storage, administrative and support service activities 3.0% 8.5% Technology, telecommunications 2.0% 5.5% Health care, utilities, professional and technical activities 1.5% 5.0% Other sector 5.0% 12.0% Full version of the BA-CVA (hedges are recognized)
11.17. As set out in 11.13(1) the full version of the BA-CVA recognizes the effect of counterparty credit spread hedges. Only transactions used for the purpose of mitigating the counterparty credit spread component of CVA risk, and managed as such, can be eligible hedges.
11.18. Only single-name credit default swaps (CDS), single-name contingent CDS and index CDS can be eligible CVA hedges.
11.19. Eligible single-name credit instruments must:
(1) reference the counterparty directly; or
(2) reference an entity legally related to the counterparty; where legally related refers to cases where the reference name and the counterparty are either a parent and its subsidiary or two subsidiaries of a common parent; or
(3) reference an entity that belongs to the same sector and region as the counterparty.
11.20. Banks that intend to use the full version of BA-CVA must calculate the reduced version (Kreduced) as well. Under the full version, capital requirement for CVA risk DSBA-CVA × Kfull is calculated as follows, where DSBA-CVA = 0.65, and β= 0.25 is the SAMA supervisory parameter that is used to provide a floor that limits the extent to which hedging can reduce the capital requirements for CVA risk:
Kfull = β ∙ Kreduced + (1 - β) ∙ Khedged
11.21. The part of capital requirements that recognizes eligible hedges (Khedged) is calculated formulas follows (where the summations are taken over all counterparties c that are within scope of the CVA charge), where:
(1) Both the stand-alone CVA capital (SCVAc) and the correlation parameter (ρ) are defined in exactly the same way as for the reduced form calculation BA-CVA.
(2) SNHc is a quantity that gives recognition to the reduction in CVA risk of the counterparty c arising from the bank's use of single-name hedges of credit spread risk. See 11.23 for its calculation.
(3) IH is a quantity that gives recognition to the reduction in CVA risk across all counterparties arising from the bank's use of index hedges. See 11.24 for its calculation.
(4) HMAc is a quantity characterizing hedging misalignment, which is designed to limit the extent to which indirect hedges can reduce capital requirements given that they will not fully offset movements in a counterparty's credit spread. That is, with indirect hedges present Khedged cannot reach zero. See 11.25 for its calculation.
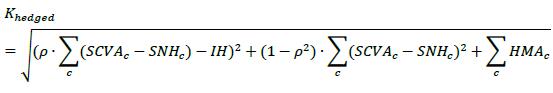
11.22. The formula for Khedged in 11.21 comprises three main terms as below:
(1) The first term (ρ • ∑c(SCVAc - SNHc) - IH)2 aggregates the systematic components of CVA risk arising from the bank's counterparties, the single name hedges and the index hedges.
(2) The second term (1- ρ2) • ∑c(SCVAc - SNHc)2 aggregates the idiosyncratic components of CVA risk arising from the bank's counterparties and the single-name hedges.
(3) The third term ∑cHMAc aggregates the components of indirect hedges that are not aligned with counterparties' credit spreads.
11.23. The quantity SNHc is calculated as follows (where the summation is across all single name hedges h that the bank has taken out to hedge the CVA risk of counterparty c), where:
(1) rhc is the supervisory prescribed correlation between the credit spread of counterparty c and the credit spread of a single-name hedge h of counterparty c. The value of rhc is set out the table 2 of 11.26. It is set at 100% if the hedge directly reference the counterparty c, and set at lower values if it does not.
(2) MhSN is the remaining maturity of single-name hedge h.
(3) BhSN is the notional of single-name hedge h. For single-name contingent credit default swaps (CDS), the notional is determined by the current market value of the reference portfolio or instrument.
(4) DFhSN is the supervisory discount factor calculated as 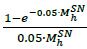 .
.
(5) RWh is the supervisory risk weight of single-name hedge h that reflects the volatility of the credit spread of the reference name of the hedging instrument. These risk weights are based on a combination of sector and credit quality of the reference name of the hedging instrument as prescribed in Table 1 of 11.16.
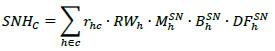
11.24. The quantity IH is calculated as follows (where the summation is across all index hedges i that the bank has taken out to hedge CVA risk), where:
(1) Miind is the remaining maturity of index hedge i.
(2) Biind is the notional of the index hedge i.
(3) DFiind is the supervisory discount factor calculated as 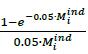
(4) RWi is the supervisory risk weight of the index hedge i. RWi is taken from the Table 1 of 11.16 based on the sector and credit quality of the index constituents and adjusted as follows:
(a) For an index where all index constituents belong to the same sector and are of the same credit quality, the relevant value in the Table 1 of 11.16 is multiplied by 0.7 to account for diversification of idiosyncratic risk within the index.
(b) For an index spanning multiple sectors or with a mixture of investment grade constituents and other constituents, the name-weighted average of the risk weights from the Table 1 of 11.16 should be calculated and then multiplied by 0.7.
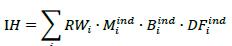
11.25. The quantity HMAc is calculated as follows(where the summation is across all single name hedges h that have been taken out to hedge the CVA risk of counterparty c), where rhc, MhSN, BhSN, DFhSN and RWh have the same definitions as set out in 11.23.
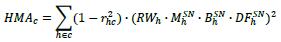
11.26. The supervisory prescribed correlations rhc between the credit spread of counterparty c and the credit spread of its single-name hedge h are set in Table 2 as follows:
Table 2: Correlations between credit spread of counterparty and single-name hedge Single-name hedge h of counterparty c Value of rhc references counterparty c directly 100% has legal relation with counterparty c 80% shares sector and region with counterparty c 50% 41 One of the basic assumptions underlying the BA-CVA is that systematic credit spread risk is driven by a single factor. Under this assumption, ρ can be interpreted as the correlation between the credit spread of a counterparty and the single credit spread systematic factor.
42 DF is SAMA discount factor averaged over time between today and the netting set's effective maturity date. The interest rate used for discounting is set at 5%, hence 0.05 in the formula. The product of EAD and effective maturity in the BA-CVA formula is a proxy for the area under the discounted expected exposure profile of the netting set. The IMM definition of effective maturity already includes this discount factor, hence DF is set to 1 for IMM banks. Outside IMM, netting set effective maturity is defined as an average of actual trade maturities. This definition lacks discounting, so SAMA discount factor is added to compensate for this.
43 ∝ is the multiplier used to convert Effective Expected Positive Exposure (EEPE) to EAD in both SACCR and IMM. Its role in the calculation, therefore, is to convert the EAD of the netting set (EADNS) back to EEPE.Standardized Approach for Credit Valuation Adjustment Risk
11.27. The SA-CVA is an adaptation of the standardized approach for market risk set out in Chapter 6 to Chapter 9 of the Minimum Capital Requirements for Market Risk. The primary differences of the SA-CVA from the standardized approach for market risk are:
(1) The SA-CVA features a reduced granularity of market risk factors; and
(2) The SA-CVA does not include default risk and curvature risk.
11.28. Under the SA-CVA, capital requirements must be calculated and reported to SAMA at the same frequency as for the market risk standardized approach. In addition, banks using the SA-CVA must have the ability to produce SA-CVA capital requirement calculations at the request of SAMA and must accordingly provide the calculations.
11.29. The SA-CVA uses as inputs the sensitivities of regulatory CVA to counterparty credit spreads and market risk factors driving the values of covered transactions. Sensitivities must be computed by banks in accordance with the prudent valuation guidance set out in Basel Framework.
11.30. For a bank to be considered eligible for the use of SA-CVA by SAMA as set out in 11.7 of this framework, the bank must meet the following criteria at the minimum.
(1) A bank must be able to model exposure and calculate, on at least a monthly basis, CVA and CVA sensitivities to the market risk factors specified in 11.54 to 11.77 in this framework.
(2) A bank must have a CVA desk (or a similar dedicated function) responsible for risk management and hedging of CVA.
Regulatory CVA Calculations
11.31. A bank must calculate regulatory CVA for each counterparty with which it has at least one covered position for the purpose of the CVA risk capital requirements.
11.32. Regulatory CVA at a counterparty level must be calculated according to the following principles. A bank must demonstrate its compliance to the principles to SAMA.
(1) Regulatory CVA must be calculated as the expectation of future losses resulting from default of the counterparty under the assumption that the bank itself is free from the default risk. In expressing the regulatory CVA, non-zero losses must have a positive sign. This is reflected in 11.52 where WSkhdg must be subtracted from WSkCVA.
(2) The calculation must be based on at least the following three sets of inputs:
a) term structure of market-implied probability of default (PD);
b) market-consensus expected loss given default (ELGD);
c) simulated paths of discounted future exposure.
(3) The term structure of market-implied PD must be estimated from credit spreads observed in the markets. For counterparties whose credit is not actively traded (i.e. illiquid counterparties), the market-implied PD must be estimated from proxy credit spreads estimated for these counterparties according to the following requirements:
a) A bank must estimate the credit spread curves of illiquid counterparties from credit spreads observed in the markets of the counterparty's liquid peers via an algorithm that discriminates on at least the following three variables: a measure of credit quality (e.g. rating), industry, and region.
b) In certain cases, mapping an illiquid counterparty to a single liquid reference name can be allowed. A typical example would be mapping a municipality to its home country (i.e. setting the municipality credit spread equal to the sovereign credit spread plus a premium). A bank must justify to SAMA each case of mapping an illiquid counterparty to a single liquid reference name
c) When no credit spreads of any of the counterparty's peers is available due to the counterparty's specific type (e.g. project finance, funds), a bank is allowed to use a more fundamental analysis of credit risk to proxy the spread of an illiquid counterparty. However, where historical PDs are used as part of this assessment, the resulting spread cannot be based on historical PD only - it must relate to credit markets.
(4) The market-consensus ELGD value must be the same as the one used to calculate the risk-neutral PD from credit spreads unless the bank can demonstrate that the seniority of the exposure resulting from covered positions differs from the seniority of senior unsecured bonds. Collateral provided by the counterparty does not change the seniority of the exposure.
(5) The simulated paths of discounted future exposure are produced by pricing all derivative transactions with the counterparty along simulated paths of relevant market risk factors and discounting the prices to today using risk-free interest rates along the path.
(6) All market risk factors material for the transactions with a counterparty must be simulated as stochastic processes for an appropriate number of paths defined on an appropriate set of future time points extending to the maturity of the longest transaction.
(7) For transactions with a significant level of dependence between exposure and the counterparty's credit quality, this dependence should be taken into account.
(8) For margined counterparties, collateral is permitted to be recognized as a risk mitigant under the following conditions:
a) Collateral management requirements outlined in7.39 and 7.40 in this framework are satisfied.
b) All documentation used in collateralized transactions must be binding on all parties and legally enforceable in all relevant jurisdictions. Banks must have conducted sufficient legal review to verify this and have a well founded legal basis to reach this conclusion, and undertake such further review as necessary to ensure continuing enforceability.
(9) For margined counterparties, the simulated paths of discounted future exposure must capture the effects of margining collateral that is recognized as a risk mitigant along each exposure path. All the relevant contractual features such as the nature of the margin agreement (unilateral vs bilateral), the frequency of margin calls, the type of collateral, thresholds, independent amounts, initial margins and minimum transfer amounts must be appropriately captured by the exposure model. To determine collateral available to a bank at a given exposure measurement time point, the exposure model must assume that the counterparty will not post or return any collateral within a certain time period immediately prior to that time point. The assumed value of this time period, known as the margin period of risk (MPoR), cannot be less than SAMA's supervisory floor. For SFTs and client cleared transactions as specified in 8.12 in this framework, the supervisory floor for the MPoR is equal to 4+N business days, where N is the re-margining period specified in the margin agreement (in particular, for margin agreements with daily or intra-daily exchange of margin, the minimum MPoR is 5 business days). For all other transactions, the supervisory floor for the MPoR is equal to 9+N business days.
11.33. The simulated paths of discounted future exposure are obtained via the exposure models used by a bank for calculating front office/accounting CVA, adjusted (if needed) to meet the requirements imposed for regulatory CVA calculation. Model calibration process (with the exception of the MPoR), market and transaction data used for regulatory CVA calculation must be the same as the ones used for accounting CVA calculation.
11.34. The generation of market risk factor paths underlying the exposure models must satisfy and a bank must demonstrate to SAMA its compliance to the following requirements:
(1) Drifts of risk factors must be consistent with a risk-neutral probability measure. Historical calibration of drifts is not allowed.
(2) The volatilities and correlations of market risk factors must be calibrated to market data whenever sufficient data exist in a given market. Otherwise, historical calibration is permissible.
(3) The distribution of modelled risk factors must account for the possible non-normality of the distribution of exposures, including the existence of leptokurtosis (“fat tails”), where appropriate.
11.35. Netting recognition is the same as in the accounting CVA calculations. In particular, netting uncertainty can be modelled.
11.36. A bank must satisfy and demonstrate to SAMA its compliance to the following requirements:
(1) Exposure models used for calculating regulatory CVA must be part of a CVA risk management framework that includes the identification, measurement, management, approval and internal reporting of CVA risk. A bank must have a credible track record in using these exposure models for calculating CVA and CVA sensitivities to market risk factors.
(2) Senior management should be actively involved in the risk control process and must regard CVA risk control as an essential aspect of the business to which significant resources need to be devoted.
(3) A bank must have a process in place for ensuring compliance with a documented set of internal policies, controls and procedures concerning the operation of the exposure system used for accounting CVA calculations.
(4) A bank must have an independent control unit that is responsible for the effective initial and ongoing validation of the exposure models. This unit must be independent from business credit and trading units (including the CVA desk), must be adequately staffed and must report directly to senior management of the bank.
(5) A bank must document the process for initial and ongoing validation of its exposure models to a level of detail that would enable a third party to understand how the models operate, their limitations, and their key assumptions; and recreate the analysis. This documentation must set out the minimum frequency with which ongoing validation will be conducted as well as other circumstances (such as a sudden change in market behavior) under which additional validation should be conducted. In addition, the documentation must describe how the validation is conducted with respect to data flows and portfolios, what analyses are used and how representative counterparty portfolios are constructed.
(6) The pricing models used to calculate exposure for a given path of market risk factors must be tested against appropriate independent benchmarks for a wide range of market states as part of the initial and ongoing model validation process. Pricing models for options must account for the nonlinearity of option value with respect to market risk factors.
(7) An independent review of the overall CVA risk management process should be carried out regularly in the bank's own internal auditing process. This review should include both the activities of the CVA desk and of the independent risk control unit.
(8) A bank must define criteria on which to assess the exposure models and their inputs and have a written policy in place to describe the process to assess the performance of exposure models and remedy unacceptable performance.
(9) Exposure models must capture transaction-specific information in order to aggregate exposures at the level of the netting set. A bank must verify that transactions are assigned to the appropriate netting set within the model.
(10) Exposure models must reflect transaction terms and specifications in a timely, complete, and conservative fashion. The terms and specifications must reside in a secure database that is subject to formal and periodic audit. The transmission of transaction terms and specifications data to the exposure model must also be subject to internal audit, and formal reconciliation processes must be in place between the internal model and source data systems to verify on an ongoing basis that transaction terms and specifications are being reflected in the exposure system correctly or at least conservatively.
(11) The current and historical market data must be acquired independently of the lines of business and be compliant with accounting. They must be fed into the exposure models in a timely and complete fashion, and maintained in a secure database subject to formal and periodic audit. A bank must also have a well-developed data integrity process to handle the data of erroneous and/or anomalous observations. In the case where an exposure model relies on proxy market data, a bank must set internal policies to identify suitable proxies and the bank must demonstrate empirically on an ongoing basis that the proxy provides a conservative representation of the underlying risk under adverse market conditions.
Eligible hedges
11.37. Only whole transactions that are used for the purpose of mitigating CVA risk, and managed as such, can be eligible hedges. Transactions cannot be split into several effective transactions.
11.38. Eligible hedges can include:
(1) instruments that hedge variability of the counterparty credit spread; and
(2) instruments that hedge variability of the exposure component of CVA risk.
11.39. Instruments that are not eligible for the internal models approach for market risk under Chapter 10 to Chapter 13 of the Minimum Capital Requirements for Market Risk (e.g. tranched credit derivatives) cannot be eligible CVA hedges.
Multiplier
11.40. Aggregated capital requirements can be scaled up by the multiplier mCVA.
11.41. The multiplier mCVA is set at 1. SAMA may require a bank to use a higher value of mCVA if SAMA determines that the bank’s CVA model risk warrants it (e.g. if the level of model risk for the calculation of CVA sensitivities is too high or the dependence between the bank’s exposure to a counterparty and the counterparty’s credit quality is not appropriately taken into account in its CVA calculations).
Calculations
11.42. The SA-CVA capital requirements are calculated as the sum of the capital requirements for delta and vega risks calculated for the entire CVA portfolio (including eligible hedges).
11.43. The capital requirements for delta risk are calculated as the simple sum of delta capital requirements calculated independently for the following six risk classes:
(1) interest rate risk;
(2) foreign exchange (FX) risk;
(3) counterparty credit spread risk;
(4) reference credit spread risk (i.e. credit spreads that drive the CVA exposure component);
(5) equity risk; and
(6) commodity risk.
11.44. If an instrument is deemed as an eligible hedge for credit spread delta risk, it must be assigned in its entirety (see 11.37 of this framework) either to the counterparty credit spread or to the reference credit spread risk class. Instruments must not be split between the two risk classes.
11.45. The capital requirements for vega risk are calculated as the simple sum of vega capital requirements calculated independently for the following five risk classes. There is no vega capital requirements for counterparty credit spread risk.
(1) interest rate risk; (IR);
(2) FX risk;
(3) reference credit spread risk;
(4) equity risk; and
(5) commodity risk
11.46. Delta and vega capital requirements are calculated in the same manner using the same procedures set out in 11.47 to 11.53 of this framework.
11.47. For each risk class, (i) the sensitivity of the aggregate CVA, skCVA, and (ii) the sensitivity of the market value of all eligible hedging instruments in the CVA portfolio, skHdg, to each risk factor k in the risk class are calculated. The sensitivities are defined as the ratio of the change of the value in question (i.e. (i) aggregate CVA or (ii) market value of all CVA hedges) caused by a small change of the risk factor’s current value to the size of the change. Specific definitions for each risk class are set out in 11.54 to 11.77of this framework. These definitions include specific values of changes or shifts in risk factors. However, a bank may use smaller values of risk factor shifts if doing so is consistent with internal risk management calculations. A bank may use AAD and similar computational techniques to calculate CVA sensitivities under the SA-CVA if doing so is consistent with the bank’s internal risk management calculations and the relevant validation standards described in the SA-CVA framework.
11.48. CVA sensitivities for vega risk are always material and must be calculated regardless of whether or not the portfolio includes options. When CVA sensitivities for vega risk are calculated, the volatility shift must apply to both types of volatilities that appear in exposure models:
(1) volatilities used for generating risk factor paths; and
(2) volatilities used for pricing options.
11.49. If a hedging instrument is an index, its sensitivities to all risk factors upon which the value of the index depends must be calculated. The index sensitivity to risk factor k must be calculated by applying the shift of risk factor k to all index constituents that depend on this risk factor and recalculating the changed value of the index. For example, to calculate delta sensitivity of S&P500 to large financial companies, a bank must apply the relevant shift to equity prices of all large financial companies that are constituents of S&P500 and re-compute the index.
11.50. For the following risk classes, a bank may choose to introduce a set of additional risk factors that directly correspond to qualified credit and equity indices. For delta risks, a credit or equity index is qualified if it satisfies liquidity and diversification conditions specified in Chapter 7.31 of the Minimum Capital Requirements for Market Risk; for vega risks, any credit or equity index is qualified. Under this option, a bank must calculate sensitivities of CVA and the eligible CVA hedges to the qualified index risk factors in addition to sensitivities to the non-index risk factors. Under this option, for a covered transaction or an eligible hedging instrument whose underlying is a qualified index, its contribution to sensitivities to the index constituents is replaced with its contribution to a single sensitivity to the underlying index. For example, for a portfolio consisting only of equity derivatives referencing only qualified equity indices, no calculation of CVA sensitivities to non-index equity risk factors is necessary. If more than 75% of constituents of a qualified index (taking into account the weightings of the constituents) are mapped to the same sector, the entire index must be mapped to that sector and treated as a single-name sensitivity in that bucket. In all other cases, the sensitivity must be mapped to the applicable index bucket.
(1) counterparty credit spread risk;
(2) reference credit spread risk; and
(3) equity risk.
11.51. The weighted sensitivities WSkCVA and WSkHdg for each risk factor k are calculated by multiplying the net sensitivities SkCVA and SkHdg, respectively, by the corresponding risk weight RWk (the risk weights applicable to each risk class are specified in 11.54 to 11.77 of this framework).
WSkCVA = RWkskCVA
WSkHdg = RWkskHdg
11.52. The net weighted sensitivity of the CVA portfolio Sk to risk factor k is obtained by44:
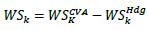
11.53. For each risk class, the net sensitivities are aggregated as follows:
(1) The weighted sensitivities must be aggregated into a capital requirement Kb within each bucket b (the buckets and correlation parameters ρKl applicable to each risk class are specified in 11.54 to 11.77 of this framework), where R is the hedging disallowance parameter, set at 0.01, that prevents the possibility of recognizing perfect hedging of CVA risk.
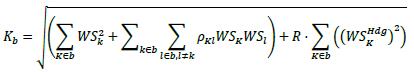
(2) Bucket-level capital requirements must then be aggregated across buckets within each risk class (the correlation parameters γbc applicable to each risk class are specified in 11.54 to 11.77 of this framework). Note that this equation differs from the corresponding aggregation equation for market risk capital requirements in Chapter 7.4 of the Minimum Capital Requirements for Market Risk, including the multiplier mCVA.
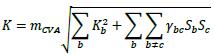
(3) In calculating K in above (2), S is defined as the sum of the weighted b sensitivities WS for all risk factors k within bucket b, floored by -K and k b capped by K, and the S is defined in the same way for all risk factors k in b c bucket c:
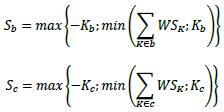
Interest rates buckets, risk factors, sensitivities, risk weights and correlations
11.54. For interest rate delta and vega risks, buckets must be set per individual currencies.
11.55. For interest rate delta and vega risks, cross-bucket correlation γbc is set at 0.5 for all currency pairs.
11.56. The interest rate delta risk factors for a bank’s reporting currency and for the following currencies USD, EUR, GBP, AUD, CAD, SEK or JPY:
(1) The interest rate delta risk factors are the absolute changes of the inflation rate and of the risk-free yields for the following five tenors: 1 year, 2 years, 5 years, 10 years and 30 years.
(2) The sensitivities to the abovementioned risk-free yields are measured by changing the risk-free yield for a given tenor for all curves in a given currency by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001. The sensitivity to the inflation rate is obtained by changing the inflation rate by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.
(3) The risk weights RWk are set as follows:
Table 3: Risk weight for interest rate risk (specified currencies) Risk factor 1 year 2 years 5 years 10 years 30 years Inflation Risk weight 1.11% 0.93% 0.74% 0.74% 0.74% 1.11% (4) The correlations between pairs of risk factors ρkl are set as follows:
Table 4: Correlations for interest rate risk factors (specified currencies) 1 year 2 years 5 years 10 years 30 years Inflation 1 year 100% 91% 72% 55% 31% 40% 2 years 100% 87% 72% 45% 40% 5 years 100% 91% 68% 40% 10 years 100% 83% 40% 30 years 100% 40% Inflation 100% 11.57. The interest rate delta risk factors for other currencies not specified in 11.56 of this framework:
(1) The interest rate risk factors are the absolute change of the inflation rate and the parallel shift of the entire risk-free yield curve for a given currency.
(2) The sensitivity to the yield curve is measured by applying a parallel shift to all risk-free yield curves in a given currency by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001. The sensitivity to the inflation rate is obtained by changing the inflation rate by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.
(3) The risk weights for both the risk-free yield curve and the inflation rate RWk are set at 1.85%.
(4) The correlations between the risk-free yield curve and the inflation rate ρKl are set at 40%.
11.58. The interest rate vega risk factors for all currencies:
(1) The interest rate vega risk factors are a simultaneous relative change of all volatilities for the inflation rate and a simultaneous relative change of all interest rate volatilities for a given currency.
(2) The sensitivity to (i) the interest rate volatilities or (ii) inflation rate volatilities is measured by respectively applying a simultaneous shift to (i) all interest rate volatilities or (ii) inflation rate volatilities by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) The risk weights for both the interest rate volatilities and the inflation rate volatilities RWk are set to 100%.
(4) Correlations between the interest rate volatilities and the inflation rate volatilities ρKl are set at 40%.
Foreign exchange buckets, risk factors, sensitivities, risk weights and correlations
11.59. For FX delta and vega risks, buckets must be set per individual currencies except for a bank’s own reporting currency.
11.60. For FX delta and vega risks, the cross-bucket correlation γbc is set at 06. for all currency pairs.
11.61. The FX delta risk factors for all currencies:
(1) The single FX delta risk factor is defined as the relative change of the FX spot rate between a given currency and a bank’s reporting currency, where the FX spot rate is the current market price of one unit of another currency expressed in the units of the bank’s reporting currency.
(2) Sensitivities to FX spot rates are measured by shifting the exchange rate between the bank’s reporting currency and another currency (i.e. the value of one unit of another currency expressed in units of the reporting currency) by 1% relative to its current value and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01. For transactions that reference an exchange rate between a pair of non-reporting currencies, the sensitivities to the FX spot rates between the bank’s reporting currency and each of the referenced non-reporting currencies must be measured.45
(3) The risk weights for all exchange rates between the bank’s reporting currency and another currency are set at 11%.
11.62. The FX vega risk factors for all currency:
(1) The single FX vega risk factor is a simultaneous relative change of all volatilities for an exchange rate between a bank’s reporting currency and another given currency.
(2) The sensitivities to the FX volatilities are measured by simultaneously shifting all volatilities for a given exchange rate between the bank’s reporting currency and another currency by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01. For transactions that reference an exchange rate between a pair of non-reporting currencies, the volatilities of the FX spot rates between the bank’s reporting currency and each of the referenced non-reporting currencies must be measured.
(3) The risk weights for FX volatilities RWk are set to 100%.
Counterparty credit spread buckets, risk factors, sensitivities, risk weights and correlations
11.63. Counterparty credit spread risk is not subject to vega risk capital requirements. Buckets for delta risk are set as follows:
(1) Buckets 1 to 7 are defined for factors that are not qualified indices as set out in 11.50 of this framework;
(2) Bucket 8 is set for the optional treatment of qualified indices. Under the optional treatment, only instruments that reference qualified indices can be assigned to bucket 8, while all single-name and all non-qualified index hedges must be assigned to buckets 1 to 7 for calculations of CVA sensitivities and sensitivities. For any instrument referencing an index assigned to buckets 1 to 7, the look-through approach must be used (i.e., sensitivity of the hedge to each index constituent must be calculated).
Table 5: Buckets for counterparty credit spread delta risk Bucket number Sector 1 a) Sovereigns including central banks, multilateral development banks b) Local government, government-backed non-financials, education and public administration 2 Financials including government-backed financials 3 Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying 4 Consumer goods and services, transportation and storage, administrative and support service activities 5 Technology, telecommunications 6 Health care, utilities, professional and technical activities 7 Other sector 8 Qualified Indices 11.64. For counterparty credit spread delta risk, cross-bucket correlations γbc are set as follows:
Table 6: Cross-bucket correlations for counterparty credit spread delta risk Bucket 1 2 3 4 5 6 7 8 1 100% 10% 20% 25% 20% 15% 0% 45% 2 100% 5% 15% 20% 5% 0% 45% 3 100% 20% 25% 5% 0% 45% 4 100% 25% 5% 0% 45% 5 100% 5% 0% 45% 6 100% 0% 45% 7 100% 0% 8 100% 11.65. The counterparty credit spread delta risk factors for a given bucket:
(1) The counterparty credit spread delta risk factors are absolute shifts of credit spreads of individual entities (counterparties and reference names for counterparty credit spread hedges) and qualified indices (if the optional treatment is chosen) for the following tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(2) For each entity and each tenor point, the sensitivities are measured by shifting the relevant credit spread by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.
(3) The risk weights RWk are set as follows the depending on the entity's bucket, where IG, HY, and NR represent “investment grade”, “high yield” and “not rated” as specified for the BA-CVA in 11.16 of this framework. The same risk weight for a given bucket and given credit quality applies to all tenors.
Table 7: Risk weights for counterparty credit spread delta risk Bucket 1 a) 1 b) 2 3 4 5 6 7 8 IG names 0.5% 1.0% 5.0% 3.0% 3.0% 2.0% 1.5% 5.0% 1.5% HY and NR names 2.0% 4.0% 12.0% 7.0% 8.5% 5.5% 5.0% 12.0% 5.0% (4) For buckets 1 to 7, the correlation parameter ρkl between two weighted sensitivities WSk and WSi is calculated as follows, where:
a) ρtenor is equal to 100% if the two tenors are the same and 90% otherwise;
b) ρname is equal to 100% if the two names are the same, 90% if the two names are distinct, but legally related and 50% otherwise;
c) ρquality is equal to 100% if the credit quality of the two names is the same (i.e. IG and IG or HY/NR and HY/NR) and 80% otherwise.
ρkl = ρtenor ∙ ρname ∙ ρquality
(5) For bucket 8, the correlation parameter ρkl between two weighted sensitivities WSk and WSi is calculated as follows, where
a) ρtenor is equal to 100% if the two tenors are the same and 90% otherwise;
b) ρname is equal to 100% if the two indices are the same and of the same series, 90% if the two indices are the same, but of distinct series, and 80% otherwise;
c) ρquality is equal to 100% if the credit quality of the two indices is the same (ie IG and IG or HY and HY) and 80% otherwise.
ρkl = ρtenor ∙ ρname ∙ ρquality
Reference credit spread buckets, risk factors, sensitivities, risk weights and correlations
11.66. Reference credit spread risk is subject to both delta and vega risk capital requirements. Buckets for delta and vega risks are set as follows, where IG, HY and NR represent “investment grade”, “high yield” and “not rated” as specified for the BA-CVA in 11.16 of this framework:
Table 8: Buckets for reference credit spread risk Bucket number Credit quality Sector 1 IG Sovereigns including central banks, multilateral development banks 2 Local government, government-backed non-financials, education and public administration 3 Financials including government-backed financials 4 Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying 5 Consumer goods and services, transportation and storage, administrative and support service activities 6 Technology, telecommunications 7 Health care, utilities, professional and technical activities 8 (HY) and NR Sovereigns including central banks, multilateral development banks 9 Local government, government-backed non-financials, education and public administration 10 Financials including government-backed financials 11 Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying 12 Consumer goods and services, transportation and storage, administrative and support service activities 13 Technology, telecommunications 14 Health care, utilities, professional and technical activities 15 (Not applicable) Other sector 16 IG Qualified Indices 17 HY Qualified Indices 11.67. For reference credit spread delta and Vega risks, cross-bucket correlations γbc are set as follows:
(1) The cross-bucket correlations γbc between buckets of the same credit quality (ie either IG or HY/NR) are set as follows:
Table 9: Cross-bucket correlations for reference credit spread risk Bucket 1/8 2/9 3/10 4/11 5/12 6/13 7/14 15 16 17 1/8 100% 75% 10% 20% 25% 20% 15% 0% 45% 45% 2/9 100% 5% 15% 20% 15% 10% 0% 45% 45% 3/10 100% 5% 15% 20% 5% 0% 45% 45% 4/11 100% 20% 25% 5% 0% 45% 45% 5/12 100% 25% 5% 0% 45% 45% 6/13 100% 5% 0% 45% 45% 7/14 100% 0% 45% 45% 15 100% 0% 0% 16 100% 75% 17 100% (2) For cross-bucket correlations γbc between buckets 1 to 14 of different credit quality (i.e. IG and HY/NR), the correlations γbc specified in 11.67 of this framework (1) are divided by 2.
11.68. Reference credit spread delta risk factors for a given bucket:
(1) The single reference credit spread delta risk factor is a simultaneous absolute shift of the credit spreads of all tenors for all reference names in the bucket.
(2) The sensitivity to reference credit spread delta risk is measured by simultaneously shifting the credit spreads of all tenors for all reference names in the bucket by 1 basis point (0.0001 in absolute terms) and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.0001.
(3) The risk weights RWk are set as follows depending on the reference name's bucket:
Table 10: Risk weights for reference credit spread delta risk IG bucket 1 2 3 4 5 6 7 8 9 Risk weigh 0.5% 1.0% 5.0% 3.0% 3.0% 2.0% 1.5% 2.0% 4.0% HY/NR bucket 10 11 12 13 14 15 16 17 Risk weight 12.0% 7.0% 8.5% 5.5% 5.0% 12.0% 1.5% 5.0% 11.69. Reference credit spread vega risk factors for a given bucket:
(1) The single reference credit spread Vega risk factor is a simultaneous relative shift of the volatilities of credit spreads of all tenors for all reference names in the bucket.
(2) The sensitivity to the reference credit spread vega risk factor is measured by simultaneously shifting the volatilities of credit spreads of all tenors for all reference names in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) Risk weights for reference credit spread volatilities ??? are set to 100%.
Equity buckets, risk factors, sensitivities, risk weights and correlations
11.70. For equity delta and vega risks, buckets are set as follow, where:
(1) Market capitalization (“market cap”) is defined as the sum of the market capitalizations of the same legal entity or group of legal entities across all stock markets globally. The reference to “group of legal entities” covers cases where the listed entity is a parent company of a group of legal entities. Under no circumstances should the sum of the market capitalizations of multiple related listed entities be used to determine whether a listed entity is “large market cap” or “small market cap”.
(2) “Large market cap” is defined as a market capitalization equal to or greater than USD 2 billion and “small market cap” is defined as a market capitalization of less than USD 2 billion.
(3) The advanced economies are Canada, the United States, Mexico, the euro area, the non-euro area western European countries (the United Kingdom, Norway, Sweden, Denmark and Switzerland), Japan, Oceania (Australia and New Zealand), Singapore and Hong Kong SAR.
(4) To assign a risk exposure to a sector, banks must rely on a classification that is commonly used in the market for grouping issuers by industry sector. The bank must assign each issuer to one of the sector buckets in the table above and it must assign all issuers from the same industry to the same sector. Risk positions from any issuer that a bank cannot assign to a sector in this fashion must be assigned to the “other sector” (i.e. bucket 11). For multinational multi-sector equity issuers, the allocation to a particular bucket must be done according to the most material region and sector in which the issuer operates.
Table 11: Buckets for equity risk Bucket number Size Region Sector 1 Large Emerging market economies Consumer goods and services, transportation and storage, administrative and support service activities, healthcare, utilities 2 Telecommunications, industrials 3 Basic materials, energy, agriculture, manufacturing, mining and quarrying 4 Financials including government-backed financials, real estate activities, technology 5 Advanced economies Consumer goods and services, transportation and storage, administrative and support service activities, healthcare, utilities 6 Telecommunications, industrials 7 Basic materials, energy, agriculture, manufacturing, mining and quarrying 8 Financials including government-backed financials, real estate activities, technology 9 Small Emerging market economies All sectors described under bucket numbers 1, 2, 3, and 4 10 Advanced economies All sectors described under bucket numbers 5, 6, 7, and 8 11 (Not applicable) Other sector 12 Large cap, advanced economies Qualified Indices 13 Other Qualified Indices 11.71. For equity delta and vega risks, cross-bucket correlation γbc is set at 15% for all cross-bucket pairs that fall within bucket numbers 1 to 10. The cross-bucket correlation between buckets 12 and 13 is set at 75% and the cross bucket correlation between buckets 12 or 13 and any of the buckets 1-10 is 45%. γbc is set at 0% for all cross-bucket pairs that include bucket 11.
11.72. Equity delta risk factors for a given bucket:
(1) The single equity delta risk factor is a simultaneous relative shift of equity spot prices for all reference names in the bucket.
(2) The sensitivity to the equity delta risk factors is measured by simultaneously shifting the equity spot prices for all reference names in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) Risk weights RWk are set as follows depending on the reference name's bucket:
Table 12: Risk weights for equity delta risk Bucket number Risk weight 1 55% 2 60% 3 45% 4 55% 5 30% 6 35% 7 40% 8 50% 9 70% 10 50% 11 70% 12 15% 13 25% 11.73. Equity Vega risk factors for a given bucket:
(1) The single equity vega risk factor is a simultaneous relative shift of the volatilities for all reference names in the bucket.
(2) The sensitivity to equity vega risk factors are measured by simultaneously shifting the volatilities for all reference names in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) The risk weights for equity volatilities RWk are set to 78% for large market capitalization buckets and to 100% for other buckets.
Commodity buckets, risk factors, sensitivities, risk weights and correlations
11.74. For commodity delta and vega risks, buckets are set as follows:
Table 13: Buckets for commodity risk Bucket number Commodity group Examples 1 Energy – Solid combustibles coal, charcoal, wood pellets, nuclear fuel (such as uranium) 2 Energy – Liquid combustibles crude oil (such as Light-sweet, heavy, WTI and Brent); biofuels (such as bioethanol and biodiesel); petrochemicals (such as propane, ethane, gasoline, methanol and butane); refined fuels (such as jet fuel, kerosene, gasoil, fuel oil, naptha, heating oil and diesel) 3 Energy – Electricity and carbon trading electricity (such as spot, day-ahead, peak and off-peak); carbon emissions trading (such as certified emissions reductions, in delivery month EUA, RGGI CO2 allowance and renewable energy certificates) 4 Freight dry-bulk route (such as capesize, panamex, handysize and supramax); liquid-bulk/gas shipping route (such as suezmax, aframax and very large crude carriers) 5 Metals – nonprecious base metal (such as aluminum, copper, lead, nickel, tin and zinc); steel raw materials (such as steel billet, steel wire, steel coil, steel scrap and steel rebar, iron ore, tungsten, vanadium, titanium and tantalum); minor metals (such as cobalt, manganese, molybdenum) 6 Gaseous combustibles natural gas; liquefied natural gas 7 Precious metals (including gold) gold; silver; platinum; palladium 8 Grains & oilseed corn; wheat; soybean (such as soybean seed, soybean oil and soybean meal); oats; palm oil; canola; barley; rapeseed (such as rapeseed seed, rapeseed oil, and rapeseed meal); red bean, sorghum; coconut oil; olive oil; peanut oil; sunflower oil; rice 9 Livestock & dairy cattle (such live and feeder); poultry; lamb; fish; shrimp; dairy (such as milk, whey, eggs, butter and cheese) 10 Softs and other agriculturals cocoa; coffee (such as arabica and robusta); tea; citrus and orange juice; potatoes; sugar; cotton; wool; lumber and pulp; rubber 11 Other commodity industrial minerals (such as potash, fertilizer and phosphate rocks), rare earths; terephthalic acid; flat glass 11.75. For commodity delta and vega risks, cross-bucket correlation γbc is set at 20% for all cross-bucket pairs that fall within bucket numbers 1 to 10. γbc is set at 0% for all cross-bucket pairs that include bucket 11.
11.76. Commodity delta risk factors for a given bucket:
(1) The single commodity delta risk factor is a simultaneous relative shift of commodity spot prices for all commodities in the bucket.
(2) The sensitivities to commodity delta risk factors are measured by shifting the spot prices of all commodities in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) The risk weights RWk are set as follows depending on the reference name's bucket:
Table 14: Risk weights for commodity delta risk Bucket 1 2 3 4 5 6 7 8 9 10 11 RW 30% 35% 60% 80% 40% 45% 20% 35% 25% 35% 50% 11.77. Commodity vega risk factors for a given bucket:
(1) The single commodity vega risk factor is a simultaneous relative shift of the volatilities for all commodities in the bucket.
(2) The sensitivity to commodity vega risk factors is measured by simultaneously shifting the volatilities for all commodities in the bucket by 1% relative to their current values and dividing the resulting change in the aggregate CVA (or the value of CVA hedges) by 0.01.
(3) Risk weights for commodity volatilities RWk are set to 100%.
44 Note that the formula in 11.52 is set out under the convention that the CVA is positive as specified in 11.32 (1). It intends to recognize the risk reducing effect of hedging. For example, when hedging the counterparty credit spread component of CVA risk for a specific counterparty by buying credit protection on the counterparty: if the counterparty’s credit spread widens, the CVA (expressed as a positive value) increases resulting in the positive CVA sensitivity to the counterparty credit spread. At the same time, as the value of the hedge from the bank’s perspective increases as well (as credit protection becomes more valuable), the sensitivity of the hedge is also positive. The positive weighted sensitivities of the CVA and its hedge offset each other using the formula with the minus sign. If CVA loss had been expressed as a negative value, the minus sign in 11.52 would have been replaced by a plus sign.
45 For example, if a SAR-reporting bank holds an instrument that references the USD-GBP exchange rate, the bank must measure CVA sensitivity both to the SAR-GBP exchange rate and to the SAR- USD exchange rate.Application Guidance/ Illustrative Examples
12. The Application of the (SA-CCR) to Sample Portfolios
12.1. This section sets out the calculation of exposure at default (EAD) for five sample portfolios using SA-CCR. The calculations for the sample portfolios assume that intermediate values are not rounded (i.e. the actual results are carried through in sequential order). However, for ease of presentation, these intermediate values as well as the final EAD are rounded.
12.2. The EAD for all netting sets in SA-CCR is given by the following formula, where alpha is assigned a value of 1.4:
EAD = alpha * (RC + multiplier * AddOnaggregate
Example 1: Interest rate derivatives (unmargined netting set)
12.3. Netting set 1 consists of three interest rates derivatives: two fixed versus floating interest rate swaps and one purchased physically-settled European swaption. The table below summarizes the relevant contractual terms of the three derivatives. All notional amounts and market values in the table are given in USD thousands.
Trade # Nature Residual maturity Base currency Notional (USD thousands) Pay Leg (*) Receive Leg (*) Market value (USD thousands) 1 Interest Rate Swap 10 years USD 10,000 Fixed Floating 30 2 Interest Rate Swap 4 years USD 10,000 Floating Fixed -20 3 European Swaption 1 into 10 years EUR 5,000 Floating Fixed 50 (*) For the swaption, the legs are those of the underlying swap 12.4. The netting set is not subject to a margin agreement and there is no exchange of collateral (independent amount/initial margin) at inception. For unmargined netting sets, the replacement cost is calculated using the following formula, where:
(1) V is a simple algebraic sum of the derivatives' market values at the reference date
(2) C is the haircut value of the initial margin, which is zero in this example
RC = max{V - C; 0}
12.5. Thus, using the market values indicated in the table (expressed in USD thousands):
RC = max{30 — 20 + 50 — 0; 0} = 60
12.6. Since V-C is positive (i.e. USD 60,000), the value of the multiplier is 1, as explained in 6.24.
12.7. The remaining term to be calculated in the calculation EAD is the aggregate add-on (AddOnaggregate). All the transactions in the netting set belong to the interest rate asset class. The AddOnaggregate for the interest rate asset class can be calculated using the seven steps set out in 6.60.
12.8. Step 1: Calculate the effective notional for each trade in the netting set. This is calculated as the product of the following three terms:
(i) the adjusted notional of the trade (d);
(ii) the supervisory delta adjustment of the trade (δ); and
(iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di = di * MFi * δ.
12.9. For interest rate derivatives, the trade-level adjusted notional (di) is the product of the trade notional amount and the supervisory duration (SDi), i.e. di = notional * SDi. The supervisory duration is calculated using the following formula, where:
(1) Si and Ei are the start and end dates, respectively, of the time period referenced by the interest rate derivative (or, where such a derivative references the value of another interest rate instrument, the time period determined on the basis of the underlying instrument). If the start date has occurred (e.g. an ongoing interest rate swap), Si must be set to zero.
(2) The calculated value of SDi is floored at 10 business days (which expressed in years, using an assumed market convention of 250 business days a year is 10/250 years
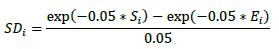
12.10. Using the formula for supervisory duration above, the trade-level adjusted notional amounts for each of the trades in Example 1 are as follows:
Trade # Notional (USD thousand) Si Ei SDi Adjusted notional, di (USD thousands) 1 10,000 0 10 7.87 78,694 2 10,000 0 4 3.63 36,254 3 5,000 1 11 7.49 37,428 12.11. 6.51 sets out the calculation of the maturity factor (MFi) for unmargined trades. For trades that have a remaining maturity in excess of one year, which is the case for all trades in this example, the formula gives a maturity factor of 1.
12.12. As set out in 6.40 to 6.43, a supervisory delta is assigned to each trade. In particular:
(1) Trade 1 is long in the primary risk factor (the reference floating rate) and is not an option so the supervisory delta is equal to 1.
(2) Trade 2 is short in the primary risk factor and is not an option; thus, the supervisory delta is equal to -1.
(3) Trade 3 is an option to enter into an interest rate swap that is short in the primary risk factor and therefore is treated as a bought put option. As such, the supervisory delta is determined by applying the relevant formula in 6.42, using 50% as the supervisory option volatility and 1 (year) as the option exercise date. In particular, assuming that the underlying price (the appropriate forward swap rate) is 6% and the strike price (the swaption's fixed rate) is 5%, the supervisory delta is:
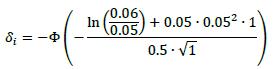
12.13. The effective notional for each trade in the netting set (Di) is calculated using the formula Di = di * MFi * δi and values for each term noted above. The results of applying the formula are as follows:
Trade # Notional (USD thousands) Adjusted notional, di (USD, thousands) Maturity Factor, MFi Delta, δi Effective notional, Di (USD, thousands) 1 10,000 78,694 1 1 78,694 2 10,000 36,254 1 -1 -36,254 3 5,000 37,428 1 -0.2694 -10,083 12.14. Step 2: Allocate the trades to hedging sets. In the interest rate asset class the hedging sets consist of all the derivatives that reference the same currency. In this example, the netting set is comprised of two hedging sets, since the trades refer to interest rates denominated in two different currencies (USD and EUR).
12.15. Step 3: Within each hedging set allocate each of the trades to the following three maturity buckets: less than one year (bucket 1), between one and five years (bucket 2) and more than five years (bucket 3). For this example, within the hedging set “USD”, trade 1 falls into the third maturity bucket (more than 5 years) and trade 2 falls into the second maturity bucket (between one and five years). Trade 3 falls into the third maturity bucket (more than 5 years) of the hedging set “EUR”. The results of steps 1 to 3 are summarized in the table below:
Trade # Effective notional, Di (USD, thousands) Hedging set Maturity bucket 1 78,694 USD 3 2 -36,254 USD 2 3 -10,083 EUR 3 12.16. Step 4: Calculate the effective notional of each maturity bucket (DB1, DB2 and DB3) within each hedging set (USD and EUR) by adding together all the trade level effective notionals within each maturity bucket in the hedging set. In this example, there are no maturity buckets within a hedging set with more than one trade, and so this case the effective notional of each maturity bucket is simply equal to the effective notional of the single trade in each bucket. Specifically:
(1) For the USD hedging set: DB1 is zero, DB2 is -36,254 (thousand USD) and DB3 is 78,694 (thousand USD)
(2) For the EUR hedging set: DB1 and DB2 are zero and DB3 is -10,083 (thousand USD).
12.17. Step 5: Calculate the effective notional of the hedging set (ENHS) by using either of the two following aggregation formulas (the latter is to be used if the bank chooses not to recognize offsets between long and short positions across maturity buckets):
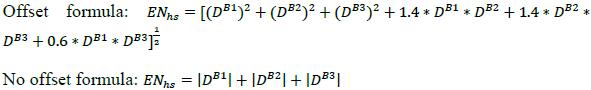
12.18. In this example, the first of the two aggregation formulas is used. Therefore, the effective notionals for the USD hedging set (ENUSD) and the EUR hedging (ENEUR) are, respectively (expressed in USD thousands):
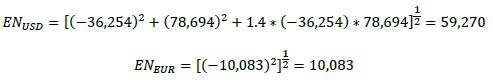
12.19. Step 6: Calculate the hedging set level add-on (AddOnhs) by multiplying the effective notional of the hedging set (ENhs) by the prescribed supervisory factor (SFhs). The prescribed supervisory factor in the interest rate asset class is set at 0.5%. Therefore, the add-on for the USD and EUR hedging sets are, respectively (expressed in USD thousands):
AddOnUSD = 59,270 ∗ 0.005 = 296.35
AddOnEUR = 10,083 ∗ 0.005 = 50.415
12.20. Step 7: Calculate the asset class level add-on (AddOnIR) by adding together all of the hedging set level add-ons calculated in step 6. Therefore, the add-on for the interest rate asset class is (expressed in USD thousands):
AddOnIR = 296.35 + 50.415 = 347
12.21. For this netting set the interest rate add-on is also the aggregate add-on because there are no derivatives belonging to other asset classes. The EAD for the netting set can now be calculated using the formula set out in 12.2 (expressed in USD thousands):
EAD = alpha * (RC + multip; ier * AddOnaggregate) = 1.4 * (60 + 1 * 347) = 569
Example 2: Credit derivatives (unmargined netting set)
12.22. Netting set 2 consists of three credit derivatives: one long single-name credit default swap (CDS) written on Firm A (rated AA), one short single-name CDS written on Firm B (rated BBB), and one long CDS index (investment grade). The table below summarizes the relevant contractual terms of the three derivatives. All notional amounts and market values in the table are in USD thousands.
Trade # Nature Reference entity/index name Rating reference entity Residual maturity Base currency Notional (USD thousands) Position Market value (USD thousands) 1 Single name CDS Firm A AA 3 years USD 10,000 Protection buyer 20 2 Single-name CDS Firm B BBB 6 years EUR 10,000 Protection seller -40 3 CDS CDX.IG 5y Investment grade 5 years USD 10,000 Protection buyer 0 12.23. As in the previous example, the netting set is not subject to a margin agreement and there is no exchange of collateral (independent amount/IM) at inception. For unmargined netting sets, the replacement cost is calculated using the following formula, where:
(1) V is a simple algebraic sum of the derivatives' market values at the reference date
(2) C is the haircut value of the IM, which is zero in this example
RC = max{V - C; 0}
12.24. Thus, using the market values indicated in the table (expressed in USD thousands):
RC = max{20 - 40 + 0 - 0; 0} = 0
12.25. Since in this example V-C is negative (equal to V, i.e. -20,000), the multiplier will be activated (i.e. it will be less than 1). Before calculating its value, the aggregate add-on (AddOnaggregate) needs to be determined.
12.26. All the transactions in the netting set belong to the credit derivatives asset class. The AddOnaggregate for the credit derivatives asset class can be calculated using the four steps set out in 6.64.
12.27. Step 1: Calculate the effective notional for each trade in the netting set. This is calculated as the product of the following three terms: (i) the adjusted notional of the trade (d); (ii) the supervisory delta adjustment of the trade (δ); and (iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di = di * MFi * δi.
12.28. For credit derivatives, like interest rate derivatives, the trade-level adjusted notional (di) is the product of the trade notional amount and the supervisory duration (SDi), i.e. di = notional * SDi. The trade-level adjusted notional amounts for each of the trades in Example 2 are as follows:
Trade # Notional (USD thousand) Si Ei SDi Adjusted notional, di (USD thousands) 1 10,000 0 3 2.79 27,858 2 10,000 0 6 5.18 51,836 3 5,000 0 5 4.42 44,240 12.29. 6.51 sets out the calculation of the maturity factor (MFi) for unmargined trades. For trades that have a remaining maturity in excess of one year, which is the case for all trades in this example, the formula gives a maturity factor of 1.
12.30. As set out in 6.40 to 6.43, a supervisory delta is assigned to each trade. In particular:
(1) Trade 1 and Trade 3 are long in the primary risk factors (CDS spread) and are not options so the supervisory delta is equal to 1 for each trade.
(2) Trade 2 is short in the primary risk factor and is not an option; thus, the supervisory delta is equal to -1.
12.31. The effective notional for each trade in the netting set (Di) is calculated using the formula Di = di * MFi * δi and values for each term noted above. The results of applying the formula are as follows:
Trade # Notional (USD thousands) Adjusted notional, di (USD, thousands) Maturity Factor,MFi Delta, δi Effective notional, Di (USD, thousands) 1 10,000 27,858 1 1 27,858 2 10,000 51,836 1 -1 -51,836 3 10,000 44,240 1 1 44,240 12.32. Step 2: Calculate the combined effective notional for all derivatives that reference the same entity. The combined effective notional of the entity (ENentity) is calculated by adding together the trade level effective notionals calculated in step 1 that reference that entity. However, since all the derivatives refer to different entities (single names/indices), the effective notional of the entity is simply equal to the trade level effective notional (Di) for each trade.
12.33. Step 3: Calculate the add-on for each entity (AddOnentity) by multiplying the entity level effective notional in step 2 by the supervisory factor that is specified for that entity (SFentity). The supervisory factors are set out in table 2 in 6.75. A supervisory factor is assigned to each single-name entity based on the rating of the reference entity (0.38% for AA-rated firms and 0.54% for BBB-rated firms). For CDS indices, the SF is assigned according to whether the index is investment or speculative grade; in this example, its value is 0.38% since the index is investment grade. Thus, the entity level add-ons are the following (USD thousands):
Reference Entity Effective notional, Di (USD, thousands) Supervisory factor, SFentity Entity-level add-on,
AddOnentity (= Di ∗ SFentity)
Firm A 27,858 0.38% 106 Firm B -51,836 0.54% -280 CDX.IG 44,240 0.38% 168 12.34. Step 4: Calculate the asset class level add-on (AddOncredit) by using the formula that follows, where:
(1) The summations are across all entities referenced by the derivatives.
(2) AddOnentity is the add-on amount calculated in step 3 for each entity referenced by the derivatives.
(3) ρentity is the supervisory prescribed correlation factor corresponding to the entity. As set out in Table 2 in 6.75, the correlation factor is 50% for single entities (Firm A and Firm B) and 80% for indexes (CDX.IG).
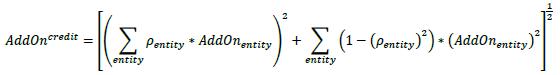
12.35. The following table shows a simple way to calculate of the systematic and idiosyncratic components in the formula:
Reference Entity Pentity AddOnentity Pentity∗ AddOnentity 1 − (Pentity)2 (AddOnentity )2 (1 − (Pentity )2 ∗ (AddOnentity )2 Firm A 0.5 106 52.9 0.75 11,207 8,405 Firm B 0.5 -280 -140 0.75 78,353 58,765 CDX.IG 0.8 168 134.5 0.36 28,261 101,174 Sum= 47.5 77,344 (Sum)2= 2,253 12.36. According to the calculations in the table, the systematic component is 2,253, while the idiosyncratic component is 77,344. Thus, the add-on for the credit asset class is calculated as follows:
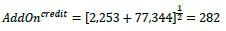
12.37. For this netting set the credit add-on (AddOncredit) is also the aggregate add-on (AddOnaggregate) because there are no derivatives belonging to other asset classes.
12.38. The value of the multiplier can now be calculated as follows, using the formula set out in 6.25:
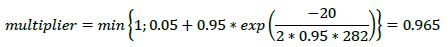
12.39. Finally, aggregating the replacement cost and the potential future exposure (PFE) component and multiplying the result by the alpha factor of 1.4, the EAD is as follows (USD thousands):
EAD = 1.4 ∗ (0 + 0.965 ∗ 282) = 381
Example 3: Commodity derivatives (unmargined netting set)
12.40. Netting set 3 consists of three commodity forward contracts. The table below summarizes the relevant contractual terms of the three derivatives. All notional amounts and market values in the table are in USD thousands.
Trade # Notional Nature Underlying Direction Residual maturity Market value 1 10,000 Forward (West Texas Intermediate, or WTI) Crude Oil Long 9 months -50 2 20,000 Forward (Brent) Crude Oil Short 2 years -30 3 10,000 Forward Silver Long 5 years -100 12.41. As in the previous two examples, the netting set is not subject to a margin agreement and there is no exchange of collateral (independent amount/IM) at inception. Thus, the replacement cost is given by:
RC = max{V — C; 0} = max{100 — 30 — 50 — 0; 0} = 20
12.42. Since V-C is positive (i.e. USD 20,000), the value of the multiplier is 1, as explained in 6.24.
12.43. All the transactions in the netting set belong to the commodities derivatives asset class. The AddOnaggregate for the commodities derivatives asset class can be calculated using the six steps set out in 6.72.
12.44. Step 1: Calculate the effective notional for each trade in the netting set. This is calculated as the product of the following three terms: (i) the adjusted notional of the trade (d); (ii) the supervisory delta adjustment of the trade (S); and (iii) the maturity factor (MF). That is, for each trade i, the effective notional DiD is calculated as Di = di * MFi * δi
12.45. For commodity derivatives, the adjusted notional is defined as the product of the current price of one unit of the commodity (e.g. barrel of oil) and the number of units referenced by the derivative. In this example, for the sake of simplicity, it is assumed that the adjusted notional (di) is equal to the notional value.
12.46. 6.51 sets out the calculation of the maturity factor (MFi) for unmargined trades. For trades that have a remaining maturity in excess of one year (trades 2 and 3 in this example), the formula gives a maturity factor of 1. For trade 1 the formula gives the following maturity factor:
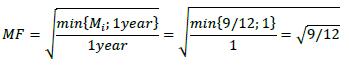
12.47. As set out in 6.40 to 6.43, a supervisory delta is assigned to each trade. In particular:
(1) Trade 1 and Trade 3 are long in the primary risk factors (WTI Crude Oil and Silver respectively) and are not options so the supervisory delta is equal to 1 for each trade.
(2) Trade 2 is short in the primary risk factor (Brent Crude Oil) and is not an option; thus, the supervisory delta is equal to -1.
Trade # Notional (USD thousands) Adjusted notional, di (USD, thousands) Maturity Factor, MFi Delta, δi Effective notional, Di (USD, thousands) 1 10,000 10,000 (9/12)0.5 1 8,660 2 20,000 20,000 1 -1 -20,000 3 10,000 10,000 1 1 10,000 12.48. Step 2: Allocate the trades in commodities asset class to hedging sets. In the commodities asset class there are four hedging sets consisting of derivatives that reference: energy (trades 1 and 2 in this example), metals (trade 3 in this example), agriculture and other commodities.
Hedging set Commodity type Trades Energy Crude oil 1 and 2 Natural gas None Coal None Electricity None Metals Silver 3 Gold None ... ... Agriculture ... ... ... ... Other ... ... Trade # Effective notional, Di (USD thousands) Hedging set Commodity type 1 8,660 Energy Crude oil 2 -20,000 Energy Crude Oil 3 10,000 Metal Silver 12.49. Step 3: Calculate the combined effective notional for all derivatives with each hedging set that reference the same commodity type. The combined effective notional of the commodity type (ENcomType) is calculated by adding together the trade level effective notionals calculated in step 1 that reference that commodity type. For purposes of this calculation, the bank can ignore the basis difference between the WTI and Brent forward contracts since they belong to the same commodity type, “Crude Oil” (unless the national supervisor requires the bank to use a more refined definition of commodity types). This step gives the following:
(1) ENCrudeOil = 8,660 + (—20,000) = —11,340
(2) ENSilver = 10,000
12.50. Step 4: Calculate the add-on for each commodity type (AddOncomType) within each hedging set by multiplying the combined effective notional for that commodity calculated in step 3 by the supervisory factor that is specified for that commodity type (SFcomType). The supervisory factors are set out in table 2 in 6.75 and are set at 40% for electricity derivatives and 18% for derivatives that reference all other types of commodities. Therefore:
(1) AddOnCrudeOil = -11,340 * 0.18 = -2,041
(2) AddOnSilver = 10,000 * 0.18 = 1,800
12.51. Step 5: Calculate the add-on for each of the four commodity hedging sets (AddOnHS) by using the formula that follows. In the formula:
(1) The summations are across all commodity types within the hedging set.
(2) AddOnComType is the add-on amount calculated in step 4 for each commodity type.
(3) ρComType is the supervisory prescribed correlation factor corresponding to the commodity type. As set out in Table 2 in 6.75, the correlation factor is set at 40% for all commodity types.

12.52. In this example, however, there is only one commodity type within the “Energy” hedging set (ie Crude Oil). All other commodity types within the energy hedging set (eg coal, natural gas etc) have a zero add-on. Therefore, the add-on for the energy hedging set is calculated as follows:
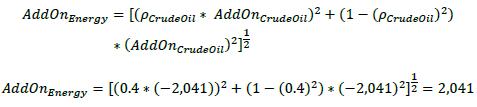
12.53. The calculation above shows that, when there is only one commodity type within a hedging set, the hedging-set add-on is equal (in absolute value) to the commodity-type add-on.
12.54. Similarly, “Silver” is the only commodity type in the “Metals” hedging set, and so the add-on for the metals hedging set is:
AddOnMetals = |AddOnSilver| = 1,800
12.55. Step 6: Calculate the asset class level add-on (AddOnCommodity) by adding together all of the hedging set level add-ons calculated in step 5:
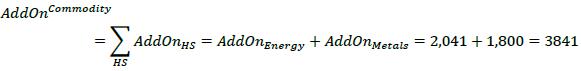
12.56. For this netting set the commodity add-on (AddOnCommodity) is also the aggregate add-on (AddOnaggregate) because there are no derivatives belonging to other asset classes.
12.57. Finally, aggregating the replacement cost and the PFE component and multiplying the result by the alpha factor of 1.4, the EAD is as follows (USD thousands):
EAD = 1.4 * (20 + 1 ∗ 3,841) = 5,406
Example 4: Interest rate and credit derivatives (unmargined netting set)
12.58. Netting set 4 consists of the combined trades of Examples 1 and 2. There is no margin agreement and no collateral. The replacement cost of the combined netting set is:
RC = max{V - C;0} = max{30 − 20 + 50 + 20 − 40 + 0; 0} = 40
12.59. The aggregate add-on for the combined netting set is the sum of add-ons for each asset class. In this case, there are two asset classes, interest rates and credit, and the add-ons for these asset classes have been copied from Examples 1 and 2:
AddOnaggregate = AddOnIR + AddOncredit = 347 + 282 = 629
12.60. Because V-C is positive, the multiplier is equal to 1. Finally, the EAD can be calculated as:
EAD = 1.4 * (40 + 1 * 629) = 936
Example 5: Interest rate and commodities derivatives (unmargined netting set)
12.61. Netting set 5 consists of the combined trades of Examples 1 and 3. However, instead of being unmargined (as assumed in those examples), the trades are subject to a margin agreement with the following specifications:
Margin frequency Threshold, TH Minimum Transfer Amount, MTA Independent Amount, IA Total net collateral held by bank (USD thousands) (USD thousands) (USD thousands) Weekly 0 5 150 200 12.62. The above table depicts a situation in which the bank received from the counterparty a net independent amount of 150 (taking into account the net amount of initial margin posted by the counterparty and any unsegregated initial margin posted by the bank). The total net collateral (after the application of haircuts) currently held by the bank is 200, which includes 50 for variation margin (VM) received and 150 for the net independent amount.
12.63. First, we determine the replacement cost. The net collateral currently held is 200 and the net independent collateral amount (NICA) is equal to the independent amount (that is, 150). The current market value of the trades in the netting set (V) is 80, it is calculated as the sum of the market value of the trades, i.e. 30 - 20 + 50 - 50 - 30 + 100 = 80. The replacement cost for margined netting sets is calculated using the formula set out in 6.20. Using this formula the replacement cost for the netting set in this example is:
RC = max{V — C; TH +MTA — NICA; 0} = max{80 — 200; 0 + 5 — 150; 0} = 0
12.64. Second, it is necessary to recalculate the interest rate and commodity add-ons, based on the value of the maturity factor for margined transactions, which depends on the margin period of risk. For daily re-margining, the margin period of risk (MPOR) would be 10 days. In accordance with 6.53, for netting sets that are not subject daily margin agreements the MPOR is the sum of nine business days plus the re-margining period (which is five business days in this example). Thus the MPOR is 14 (= 9 + 5) in this example.
12.65. The re-scaled maturity factor for the trades in the netting set is calculated using the formula set out in 6.55. Using the MPOR calculated above, the maturity factor for all trades in the netting set in this example it is calculated as follows (a market convention of 250 business days in the financial year is used):
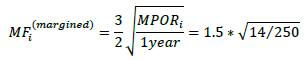
12.66. For the interest rate add-on, the effective notional for each trade (Di = di ∗ MFi ∗ Ꟙi) calculated in 12.13 must be recalculated using the maturity factor for the margined netting set calculated above. That is:
IR Trade # Notional (USD thousands) Base currency (hedging set) Maturity bucket Adjusted notional, di (USD, thousands) Maturity Factor, MFi Delta, Ꟙi Effective notional, Di (USD, thousands) 1 10,000 USD 3 78,694 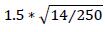
1 27,934 2 10,000 USD 2 36,254 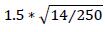
-1 -12,869 3 5,000 EUR 3 37,428 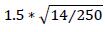
-0.2694 -3,579 12.67. Next, the effective notional of each of the three maturity buckets within each hedging set must now be calculated. However, as set out in 12.16, given that in this example there are no maturity buckets within a hedging set with more than a single trade, the effective maturity of each maturity bucket is simply equal to the effective notional of the single trade in each bucket. Specifically:
(1) For the USD hedging set: DB1 is zero, DB2 is -12,869 (thousand USD) and DB3 is 27,934 (thousand USD).
(2) For the EUR hedging set: DB1 and DB2 are zero and DB3 is -3,579 (thousand USD).
12.68. Next, the effective notional of each of the two hedging sets (USD and EUR) must be recalculated using formula set out in 12.18 and the updated values of the effective notionals of each maturity bucket. The calculation is as follows:
ENUSD = [(—12,869)2 + (27,934)2 + 1.4 * (—12,869) * 27,934]½ = 21,934
ENEUR = [(—3,579)2] ½ = 3,579
12.69. Next, the hedging set level add-ons (AddOnns) must be recalculated by multiplying the recalculated effective notionals of each hedging set (ENns) by the prescribed supervisory factor of the hedging set (SFUSD). As set out in 12.16, the prescribed supervisory factor in this case is 0.5%. Therefore, the add-on for the USD and EUR hedging sets are, respectively (expressed in USD thousands):
AddOnUSD = 21,039 * 0.005 = 105
AddOnEUR = 3,579 * 0.005 = 18
12.70. Finally, the interest rate asset class level add-on (AddOnIR) can be recalculated by adding together the USD and EUR hedging set level add-ons as follows (expressed in USD thousands):
AddOnIR = 105 + 18 = 123
12.71. The add-on for the commodity asset class must also be recalculated using the maturity factor for the margined netting. The effective notional for each trade Di = di ∗ MFi ∗ Ꟙi is set out in the table below:
IR Trade # Notional (USD thousands) Hedging
setCommodity
typeAdjusted notional, di (USD, thousands) Maturity Factor, MFi Delta, Ꟙi Effective notional, Di (USD, thousands) 1 10,000 Energy Crude Oil 10,000 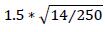
1 3,550 2 20,000 Energy Crude Oil 20,000 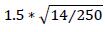
-1 -7,100 3 10,000 Metals Silver 10,000 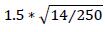
1 3,550 12.72. The combined effective notional for all derivatives with each hedging set that reference the same commodity type (ENComrype) must be recalculated by adding together the trade-level effective notionals above for each commodity type. This gives the following:
(1) ENCrudeOil = 3,550 + (-7,100) = 3,550
(2) ENSilver = 3,550
12.73. The add-on for each commodity type (AddOnCrudeOil and AddOnSilver) within each hedging set calculated in 12.50 must now be recalculated by multiplying the recalculated combined effective notional for that commodity by the relevant supervisory factor (i.e. 18%). Therefore:
(1) AddOnCrudeOil = −3,550 * 0.18 = −639
(2) AddOnSilver = 3,550 * 0.18 = −639
12.74. Next, recalculate the add-on for energy and metals hedging sets using the recalculated add-ons for each commodity type above. As noted in 12.53, given that there is only one commodity type with each hedging set, the hedging set level add on is simply equal to the absolute value of the commodity type add-on. That is:
AddOnEnergy = |AddOnCrudeOil| = 639
AddOnMetal = |AddOnSilver| = 639
12.75. Finally, calculate the commodity asset class level add-on (AddOnCommodity) by adding together the hedging set level add-ons:
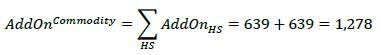
12.76. The aggregate netting set level add-on can now be calculated. As set out in 6.27, it is calculated as the sum of the asset class level add-ons. That is for this example:
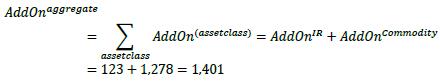
12.77. As can be seen from 12.63, the value of V-C is negative (i.e. -120) and so the multiplier will be less than 1. The multiplier is calculated using the formula set out in 6.25, which for this example gives:
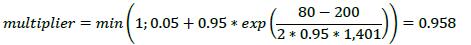
12.78. Finally, aggregating the replacement cost and the PFE component and multiplying the result by the alpha factor of 1.4, the EAD is as follows (USD thousands):
EAD = 1.4 * (0 + 0.958 * 1,401) = 1,879
13. The Effect of Standard Margin Agreements on the Calculation of Replacement Cost with SA-CCR
13.1. In this section (13.1 to 13.18), five examples are used to illustrate the operation of the SA-CCR in the context of standard margin agreements. In particular, they relate to the formulation of replacement cost for margined trades, as set out in 6.20:
RC = max{V — C; TH + MTA — NICA; 0}
Example 1
13.2. The bank currently has met all past VM calls so that the value of trades with its counterparty (€80 million) is offset by cumulative VM in the form of cash collateral received. There is a small “Minimum Transfer Amount” (MTA) of €1 million and a €0 ”Threshold” (TH). Furthermore, an “Independent Amount” (IA) of €10 million is agreed in favor of the bank and none in favor of its counterparty (i.e. the NICA is €10 million. This leads to a credit support amount of €90 million, which is assumed to have been fully received as of the reporting date.
13.3. In this example, the three terms in the replacement cost formula are:
(1) V - C =€80 million - €90 million = negative €10 million.
(2) TH + MTA - NICA = €0 + €1 million - €10 million = negative €9 million.
(3) The third term in the RC formula is always zero, which ensures that replacement cost is not negative.
13.4. The highest of the three terms (-€10 million, -€9 million, 0) is zero, so the replacement cost is zero. This is due to the large amount of collateral posted by the bank's counterparty.
Example 2
13.5. The counterparty has met all VM calls but the bank has some residual exposure due to the MTA of €1 million in its master agreement, and has a €0 TH. The value of the bank's trades with the counterparty is €80 million and the bank holds €79.5 million in VM in the form of cash collateral. In addition, the bank holds €10 million in independent collateral (here being an initial margin independent of VM, the latter of which is driven by mark-to-market (MTM) changes) from the counterparty. The counterparty holds €10 million in independent collateral from the bank, which is held by the counterparty in a non-segregated manner. The NICA is therefore €0 (= €10 million independent collateral held less €10 million independent collateral posted).
13.6. In this example, the three terms in the replacement formula are:
(1) V - C = €80 million - (€79.5 million + €10 million - €10 million)= €0.5 million.
(2) TH + MTA - NICA = €0 + €1 million - €0 = €1 million.
(3) The third term is zero.
13.7. The replacement cost is the highest of the three terms (€0.5 million, €1 million, 0) which is €1 million. This represents the largest exposure before collateral must be exchanged.
Bank as a clearing member
13.8. The case of central clearing can be viewed from a number of perspectives. One example in which the replacement cost formula for margined trades can be applied is when the bank is a clearing member and is calculating replacement cost for its own trades with a central counterparty (CCP). In this case, the MTA and TH are generally zero. VM is usually exchanged at least daily and the independent collateral amount (ICA) in the form of a performance bond or IM is held by the CCP.
Example 3
13.9. The bank, in its capacity as clearing member of a CCP, has posted VM to the CCP in an amount equal to the value of the trades it has with the CCP. The bank has posted cash as initial margin and the CCP holds the IM in a bankruptcy- remote fashion. Assume that the value of trades with the CCP are negative €50 million, the bank has posted €50 million in VM and €10 million in IM to the CCP.
13.10. Given that the IM is held by the CCP in a bankruptcy remote fashion, 6.19 permits this amount to be excluded in the calculation NICA. Therefore, the NICA is €0 because the bankruptcy-remote IM posted to the CCP can be exclude and the bank has not received any IM from the CCP. The value of C is calculated as the value of NICA plus any VM received less any VM posted. The value of C is thus negative €50 million (= €0 million + €0 million - €50 million).
13.11. In this example, the three terms in the replacement formula are:
(1) V - C = (-€50 million) - (-€50 million) = €0. That is, the negative value of the trades has been fully offset by the VM posted by the bank.
(2) TH + MTA - NICA = €0 + €0 - €0 = €0.
(3) The third term is zero.
13.12. The replacement cost is therefore €0.
Example 4
13.13. Example 4 is the same as Example 3, except that the IM posted to the CCP is not bankruptcy-remote. As a consequence, the €10 million of IM must be included in the calculation of NICA. Thus, NICA is negative €10 million (= ICA received of €0 minus unsegregated ICA posted of €10 million). Also, the value of C is negative €60 million (=NICA + VM received - VM posted = -€10 million + €0 - €50 million).
13.14. In this example, the three terms in the replacement formula are:
(1) V - C = (-€50 million) - (-€60 million) = €10 million. That is, the negative value of the trades is more than fully offset by collateral posted by the bank.
(2) TH + MTA - NICA = €0 + €0 - (-€10 million) = €10 million.
(3) The third term is zero.
13.15. The replacement cost is therefore €10 million. This represents the IM posted to the CCP which risks being lost upon default and bankruptcy of the CCP.
Example 5: Maintenance Margin Agreement
13.16. Some margin agreements specify that a counterparty (in this case, a bank) must maintain a level of collateral that is a fixed percentage of the MTM of the transactions in a netting set. For this type of margining agreement, ICA is the amount of collateral that the counterparty must maintain above the net MTM of the transactions.
13.17. For example, suppose the agreement states that a counterparty must maintain a collateral balance of at least 140% of the MTM of its transactions and that the MtM of the derivatives transactions is €50 in the bank's favor. ICA in this case is €20 (= 140% * €50 - €50). Further, suppose there is no TH, no MTA, the bank has posted no collateral and the counterparty has posted €80 in cash collateral. In this example, the three terms of the replacement cost formula are:
(1) V - C = €50 - €80 = -€30.
(2) MTA + TH - NICA = €0 + €0 - €20 = -€20.
(3) The third term is zero.
13.18. Thus, the replacement cost is zero in this example.

