7- Standardised Approach: Sensitivities-Based Method
Main Concepts of the Sensitivities-Based Method
7.1 The sensitivities of financial instruments to a prescribed list of risk factors are used to calculate the delta, vega and curvature risk capital requirements. These sensitivities are risk-weighted and then aggregated, first within risk buckets (risk factors with common characteristics) and then across buckets within the same risk class as set out in [7.8] to [7.14]. The following terminology is used in the sensitivities-based method:
(1) Risk class: seven risk classes are defined (in [7.39] to [7.89]).
(a) General interest rate risk (GIRR)
(b) Credit spread risk (CSR): non-securitisations
(c) CSR: securitisations (non-correlation trading portfolio, or non-CTP)
(d) CSR: securitisations (correlation trading portfolio, or CTP)
(e) Equity risk
(f) Commodity risk
(g) Foreign exchange (FX) risk
(2) Risk factor: variables (eg an equity price or a tenor of an interest rate curve) that affect the value of an instrument as defined in [7.8] to [7.14]
(3) Bucket: a set of risk factors that are grouped together by common characteristics (eg all tenors of interest rate curves for the same currency), as defined in [7.39] to [7.89].
(4) Risk position: the portion of the risk of an instrument that relates to a risk factor. Methodologies to calculate risk positions for delta, vega and curvature risks are set out in [7.3] to [7.5] and [7.15] to [7.26].
(a) For delta and vega risks, the risk position is a sensitivity to a risk factor.
(b) For curvature risk, the risk position is based on losses from two stress scenarios.
(5) Risk capital requirement: the amount of capital that a bank should hold as a consequence of the risks it takes; it is computed as an aggregation of risk positions first at the bucket level, and then across buckets within a risk class defined for the sensitivities-based method as set out in [7.3] to [7.7].
Instruments Subject to Each Component of the Sensitivities-Based Method
7.2 In applying the sensitivities-based method, all instruments held in trading desks as set out in [4] and subject to the sensitivities-based method (ie excluding instruments where the value at any point in time is purely driven by an exotic underlying as set out in [9.3]), are subject to delta risk capital requirements. Additionally, the instruments specified in (1) to (4) are subject to vega and curvature risk capital requirements:
(1) Any instrument with optionality11.
(2) Any instrument with an embedded prepayment option12 this is considered an instrument with optionality according to above (1). The embedded option is subject to vega and curvature risk with respect to interest rate risk and CSR (non-securitisation and securitisation) risk classes. When the prepayment option is a behavioural option the instrument may also be subject to the residual risk add-on (RRAO) as per [9]. The pricing model of the bank must reflect such behavioural patterns where relevant. For securitisation tranches, instruments in the securitised portfolio may have embedded prepayment options as well. In this case the securitisation tranche may be subject to the RRAO.
(3) Instruments whose cash flows cannot be written as a linear function of underlying notional. For example, the cash flows generated by a plain-vanilla option cannot be written as a linear function (as they are the maximum of the spot and the strike). Therefore, all options are subject to vega risk and curvature risk. Instruments whose cash flows can be written as a linear function of underlying notional are instruments without optionality (eg cash flows generated by a coupon bearing bond can be written as a linear function) and are not subject to vega risk nor curvature risk capital requirements.
(4) Curvature risks may be calculated for all instruments subject to delta risk, not limited to those subject to vega risk as specified in (1) to (3) above. For example, where a bank manages the non-linear risk of instruments with optionality and other instruments holistically, the bank may choose to include instruments without optionality in the calculation of curvature risk. This treatment is allowed subject to all of the following restrictions:
(a) Use of this approach shall be applied consistently through time.
(b) Curvature risk must be calculated for all instruments subject to the sensitivities- based method.
11 For example, each instrument that is an option or that includes an option (eg an embedded option such as convertibility or rate dependent prepayment and that is subject to the capital requirements for market risk). A non-exhaustive list of example instruments with optionality includes: calls, puts, caps, floors, swaptions, barrier options and exotic options.
12 An instrument with a prepayment option is a debt instrument which grants the debtor the right to repay part of or the entire principal amount before the contractual maturity without having to compensate for any foregone interest. The debtor can exercise this option with a financial gain to obtain funding over the remaining maturity of the instrument at a lower rate in other ways in the market.Process to Calculate the Capital Requirement Under the Sensitivities-Based Method
7.3 As set out in [7.1], the capital requirement under the sensitivities-based method is calculated by aggregating delta, vega and curvature capital requirements. The relevant paragraphs that describe this process are as follows:
(1) The risk factors for delta, vega and curvature risks for each risk class are defined in [7.8] to [7.14].
(2) The methods to risk weight sensitivities to risk factors and aggregate them to calculate delta and vega risk positions for each risk class are set out in [7.4] and [7.15] to [7.95], which include the definition of delta and vega sensitivities, definition of buckets, risk weights to apply to risk factors, and correlation parameters.
(3) The methods to calculate curvature risk are set out in [7.5] and [7.96] to [7.101], which include the definition of buckets, risk weights and correlation parameters.
(4) The risk class level capital requirement calculated above must be aggregated to obtain the capital requirement at the entire portfolio level as set out in [7.6] and [7.7].
Calculation of the delta and vega risk capital requirement for each risk class
7.4 For each risk class, a bank must determine its instruments’ sensitivity to a set of prescribed risk factors, risk weight those sensitivities, and aggregate the resulting risk-weighted sensitivities separately for delta and vega risk using the following step-by-step approach:
(1) For each risk factor (as defined in [7.8] to [7.14]), a sensitivity is determined as set out in [7.15] to [7.38].
(2) Sensitivities to the same risk factor must be netted to give a net sensitivity Sk across all instruments in the portfolio to each risk factor k. In calculating the net sensitivity, all sensitivities to the same given risk factor (eg all sensitivities to the one-year tenor point of the three-month Euribor swap curve) from instruments of opposite direction should offset, irrespective of the instrument from which they derive. For instance, if a bank’s portfolio is made of two interest rate swaps on three-month Euribor with the same fixed rate and same notional but of opposite direction, the GIRR on that portfolio would be zero.
(3) The weighted sensitivity WSk is the product of the net sensitivity Sk and the corresponding risk weight RWk as defined in [7.39] to [7.95].
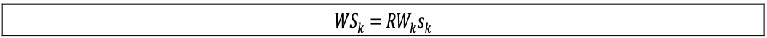
(4) Within bucket aggregation: the risk position for delta (respectively vega) bucket b, Kb, must be determined by aggregating the weighted sensitivities to risk factors within the same bucket using the prescribed correlation ρkɭ set out in the following formula, where the quantity within the square root function is floored at zero:
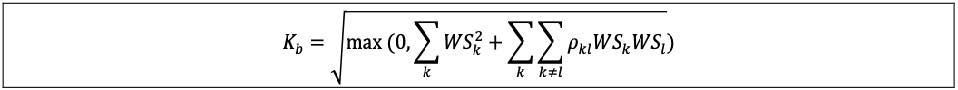
(5) Across bucket aggregation: The delta (respectively vega) risk capital requirement is calculated by aggregating the risk positions across the delta (respectively vega) buckets within each risk class, using the corresponding prescribed correlations γbc as set out in the following formula, where:
(a) Sb = ∑k WSk for all risk factors in bucket b, and Sc = ∑k WSk in bucket c.
(b) If these values for Sb and Sc described in above [7.4](5)(a) produce a negative number for the overall sum of ∑b Kb2 + ∑b ∑c≠b γbc SbSc, the bank is to calculate the delta (respectively vega) risk capital requirement using an alternative specification whereby:
(i) Sb=max [min (∑k WSk, Kb), - Kb] for all risk factors in bucket b; and
(ii) Sc=max [min (∑k WSk, Kc), - Kc] for all risk factors in bucket c.
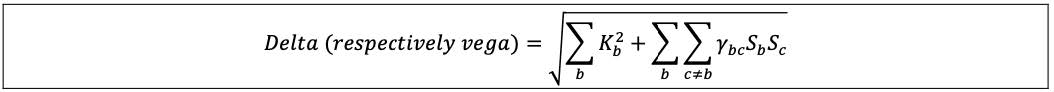
Calculation of the curvature risk capital requirement for each risk class
7.5 For each risk class, to calculate curvature risk capital requirements a bank must apply an upward shock and a downward shock to each prescribed risk factor and calculate the incremental loss for instruments sensitive to that risk factor above that already captured by the delta risk capital requirement using the following step- by-step approach:
(1) For each instrument sensitive to curvature risk factor k, an upward shock and a downward shock must be applied to k. The size of shock (ie risk weight) is set out in [7.98] and [7.99].
(a) For example for GIRR, all tenors of all the risk free interest rate curves within a given currency (eg three-month Euribor, six-month Euribor, one year Euribor, etc for the euro) must be shifted upward applying the risk weight as set out in [7.99]. The resulting potential loss for each instrument, after the deduction of the delta risk positions, is the outcome of the upward scenario. The same approach must be followed on a downward scenario.
(b) If the price of an instrument depends on several risk factors, the curvature risk must be determined separately for each risk factor.
(2) The net curvature risk capital requirement, determined by the values CVR  and CVR
and CVR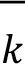 for a bank’s portfolio for risk factor k described in above [7.5] (1) is calculated by the formula below. It calculates the aggregate incremental loss beyond the delta capital requirement for the prescribed shocks, where
for a bank’s portfolio for risk factor k described in above [7.5] (1) is calculated by the formula below. It calculates the aggregate incremental loss beyond the delta capital requirement for the prescribed shocks, where
(a) i is an instrument subject to curvature risks associated with risk factor k;
(b) xk is the current level of risk factor k;
(c) Vi (Xk) is the price of instrument i at the current level of risk factor k;
(d) Vi (Xk(RW (curvature)+)) and Vi (Xk(RW (curvature)-)) denote the price of instrument i after xk is shifted (ie “shocked”) upward and downward respectively;
(e) (curvature) is the risk weight for curvature risk factor k for instrument i; and
(f) Sik is the delta sensitivity of instrument i with respect to the delta risk factor that corresponds to curvature risk factor k, where:
(i) For the FX and equity risk classes, Sik is the delta sensitivity of instrument i; and
(iii) For the GIRR, CSR and commodity risk classes, Sik is the sum of delta sensitivities to all tenors of the relevant curve of instrument i with respect to curvature risk factor k.

(3) Within bucket aggregation: the curvature risk exposure must be aggregated within each bucket using the corresponding prescribed correlation ρkɭ as set out in the following formula, where:
(a) The bucket level capital requirement (Kb) is determined as the greater of the capital requirement under the upward scenario ( 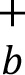 ) and the capital requirement under the downward scenario (Kb
) and the capital requirement under the downward scenario (Kb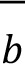 ). Notably, the selection of upward and downward scenarios is not necessarily the same across the high, medium and low correlations scenarios specified in [7.6].
). Notably, the selection of upward and downward scenarios is not necessarily the same across the high, medium and low correlations scenarios specified in [7.6].
(i) Where Kb = K 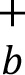 , this shall be termed “selecting the upward scenario”.
, this shall be termed “selecting the upward scenario”.
(ii) Where Kb = Kb 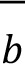 , this shall be termed “selecting the downward scenario”.
, this shall be termed “selecting the downward scenario”.
(iii) In the specific case where K 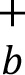 = Kb
= Kb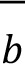 if ∑kCVR
if ∑kCVR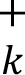 >∑k CVR
>∑k CVR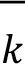 , it is deemed that the upward scenario is selected; otherwise the downward scenario is selected.
, it is deemed that the upward scenario is selected; otherwise the downward scenario is selected.
(b) Ψ(CVRk, CVRɭ) takes the value 0 if CVRk and CVRɭ both have negative signs and the value 1 otherwise.
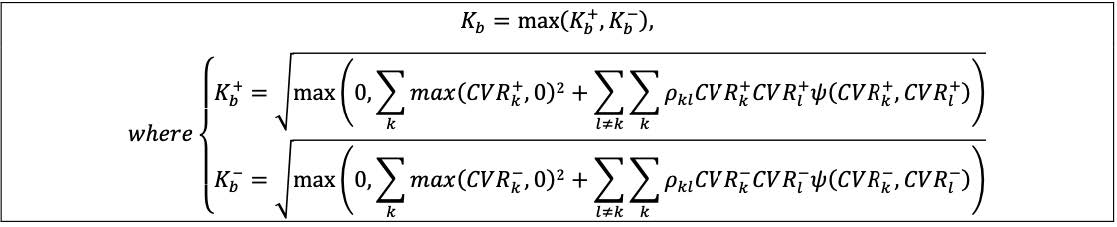
(4) Across bucket aggregation: curvature risk positions must then be aggregated across buckets within each risk class, using the corresponding prescribed correlations γbc, where:
(a) Sb = ∑k CVR 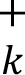 for all risk factors in bucket b, when the upward scenario has been selected for bucket b in above (3)(a). Sb = ∑k CVR
for all risk factors in bucket b, when the upward scenario has been selected for bucket b in above (3)(a). Sb = ∑k CVR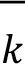 otherwise; and
otherwise; and
(b) (Sb, Sc) takes the value 0 if Sb and Sc both have negative signs and 1 otherwise.
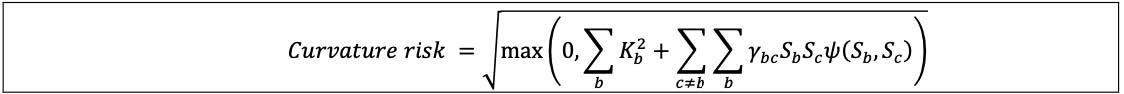
The delta used for the calculation of the curvature risk capital requirement should be the same as that used for calculating the delta risk capital requirement. The assumptions that are used for the calculation of the delta (ie sticky delta for normal or log-normal volatilities) should also be used for calculating the shifted or shocked price of the instrument.
[7.17] states that banks must determine each delta sensitivity, vega sensitivity and curvature scenario based on instrument prices or pricing models that an independent risk control unit within a bank uses to report market risks or actual profits and losses to senior management. Banks should use zero rate or market rate sensitivities consistent with the pricing models referenced in that paragraph.
Calculation of aggregate sensitivities-based method capital requirement
7.6 In order to address the risk that correlations increase or decrease in periods of financial stress, the aggregation of bucket level capital requirements and risk class level capital requirements per each risk class for delta, vega, and curvature risks as specified in [7.4] to [7.5] must be repeated, corresponding to three different scenarios on the specified values for the correlation parameter ρkɭ (correlation between risk factors within a bucket) and γbc (correlation across buckets within a risk class).
(1) Under the “medium correlations” scenario, the correlation parameters ρkɭ and γbc as specified in [7.39] to [7.101] apply.
(2) Under the “high correlations” scenario, the correlation parameters ρkɭ and γbc that are specified in [7.39] to [7.101] are uniformly multiplied by 1.25, with ρkɭ and γbc subject to a cap at 100%.
(3) Under the “low correlations” scenario, the correlation parameters ρkɭ and γbc that are specified in 7.39 to 7.101] are replaced by ρ 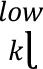 = max(2 x ρkɭ - 100%;75%x ρkɭ) γ
= max(2 x ρkɭ - 100%;75%x ρkɭ) γ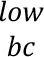 and =max(2x γbc -100%;75%x γbc).
and =max(2x γbc -100%;75%x γbc).
7.7 The total capital requirement under the sensitivities-based method is aggregated as follows:
(1) For each of three correlation scenarios, the bank must simply sum up the separately calculated delta, vega and curvature capital requirements for all risk classes to determine the overall capital requirement for that scenario.
(2) The sensitivities-based method capital requirement is the largest capital requirement from the three scenarios.
(a) For the calculation of capital requirements for all instruments in all trading desks using the standardised approach as set out in [3.10] (1) and [17.2] and [13.40], the capital requirement is calculated for all instruments in all trading desks.
(b) For the calculation of capital requirements for each trading desk using the standardised approach as if that desk were a standalone regulatory portfolio as set out in [3.8](2), the capital requirements under each correlation scenario are calculated and compared at each trading desk level, and the maximum for each trading desk is taken as the capital requirement.
Sensitivities-Based Method: Risk Factor and Sensitivity Definitions
Risk factor definitions for delta, vega and curvature risks
7.8 GIRR factors
(1) Delta GIRR: the GIRR delta risk factors are defined along two dimensions: (i) a risk-free yield curve for each currency in which interest rate-sensitive instruments are denominated and (ii) the following tenors: 0.25 years, 0.5 years, 1 year, 2 years, 3 years, 5 years, 10 years, 15 years, 20 years and 30 years, to which delta risk factors are assigned13.
(a) The risk-free yield curve per currency should be constructed using money market instruments held in the trading book that have the lowest credit risk, such as overnight index swaps (OIS). Alternatively, the risk-free yield curve should be based on one or more market- implied swap curves used by the bank to mark positions to market. For example, interbank offered rate (BOR) swap curves.
(b) When data on market-implied swap curves described in above (1)(a) are insufficient, the risk-free yield curve may be derived from the most appropriate sovereign bond curve for a given currency. In such cases the sensitivities related to sovereign bonds are not exempt from the CSR capital requirement: when a bank cannot perform the decomposition y=r+cs, any sensitivity to y is allocated both to the GIRR and to CSR classes as appropriate with the risk factor and sensitivity definitions in the standardised approach. Applying swap curves to bond-derived sensitivities for GIRR will not change the requirement for basis risk to be captured between bond and credit default swap (CDS) curves in the CSR class.
(c) For the purpose of constructing the risk-free yield curve per currency, an OIS curve (such as Eonia or a new benchmark rate) and a BOR swap curve (such as three-month Euribor or other benchmark rates) must be considered two different curves. Two BOR curves at different maturities (eg three-month Euribor and six-month Euribor) must be considered two different curves. An onshore and an offshore currency curve (eg onshore Indian rupee and offshore Indian rupee) must be considered two different curves.
(2) The GIRR delta risk factors also include a flat curve of market-implied inflation rates for each currency with term structure not recognised as a risk factor.
(a) The sensitivity to the inflation rate from the exposure to implied coupons in an inflation instrument gives rise to a specific capital requirement. All inflation risks for a currency must be aggregated to one number via simple sum.
(b) This risk factor is only relevant for an instrument when a cash flow is functionally dependent on a measure of inflation (eg the notional amount or an interest payment depending on a consumer price index). GIRR risk factors other than for inflation risk will apply to such an instrument notwithstanding.
(c) Inflation rate risk is considered in addition to the sensitivity to interest rates from the same instrument, which must be allocated, according to the GIRR framework, in the term structure of the relevant risk-free yield curve in the same currency.
(3) The GIRR delta risk factors also include one of two possible cross-currency basis risk factors14 for each currency (ie each GIRR bucket) with the term structure not recognised as a risk factor (ie both cross-currency basis curves are flat).
(a) The two cross-currency basis risk factors are basis of each currency over USD or basis of each currency over EUR. For instance, an AUD- denominated bank trading a JPY/USD cross-currency basis swap would have a sensitivity to the JPY/USD basis but not to the JPY/EUR basis.
(b) Cross-currency bases that do not relate to either basis over USD or basis over EUR must be computed either on “basis over USD” or “basis over EUR” but not both. GIRR risk factors other than for cross-currency basis risk will apply to such an instrument notwithstanding.
(c) Cross-currency basis risk is considered in addition to the sensitivity to interest rates from the same instrument, which must be allocated, according to the GIRR framework, in the term structure of the relevant risk-free yield curve in the same currency.
(4) Vega GIRR: within each currency, the GIRR vega risk factors are the implied volatilities of options that reference GIRR-sensitive underlyings; as defined along two dimensions:15
(a) The maturity of the option: the implied volatility of the option as mapped to one or several of the following maturity tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(b) The residual maturity of the underlying of the option at the expiry date of the option: the implied volatility of the option as mapped to two (or one) of the following residual maturity tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(5) Curvature GIRR:
(a) The GIRR curvature risk factors are defined along only one dimension: the constructed risk-free yield curve per currency with no term structure decomposition. For example, the euro, Eonia, three-month Euribor and six- month Euribor curves must be shifted at the same time in order to compute the euro-relevant risk-free yield curve curvature risk capital requirement. For the calculation of sensitivities, all tenors (as defined for delta GIRR) are to be shifted in parallel.
(b) There is no curvature risk capital requirement for inflation and cross-currency basis risks.
(6) The treatment described in above (1)(b) for delta GIRR also applies to vega GIRR and curvature GIRR risk factors.
Different results can be produced depending on the bank’s curve methodology as diversification will be different for different methodologies. For example, if three-month Euribor is constructed as a “spread to EONIA”, this curve will be a spread curve and can be considered a different yield curve for the purpose of computing risk-weighted PV01 and subsequent diversification. [7.8](1)(c)states that for the purpose of constructing the risk-free yield curve per currency, an overnight index swap curve (such as EONIA) and an interbank offered rate curve (such as three-month Euribor) must be considered two different curves, with distinct risk factors in each tenor bucket, for the purpose of computing the risk capital requirement.
For GIRR, CSR, equity risk, commodity risk or FX risk, risk factors need to be assigned to prescribed tenors. Banks are not permitted to perform capital computations based on internally used tenors. Risk factors and sensitivities must be assigned to the prescribed tenors. As stated in footnote 14 to [7.8] and footnote 19 to [7.25], the assignment of risk factors and sensitivities to the specified tenors should be performed by linear interpolation or a method that is most consistent with the pricing functions used by the independent risk control function of the bank to report market risks or profits and losses to senior management.
When calculating the cross-currency basis spread (CCBS) capital requirement: since pricing models use a term structure-based CCBS curve, Banks may use a term structure-based CCBS curve and aggregate sensitivities to individual tenors by simple sum.
Inflation and cross-currency bases are included in the GIRR vega risk capital requirement. As no maturity dimension is specified for the delta capital requirement for inflation or cross-currency bases (ie the possible underlying of the option), the vega risk for inflation and cross-currency bases should be considered only along the single dimension of the maturity of the option.
For the specified instruments, delta, vega and curvature capital requirements must be computed for both GIRR and CSR.
Repo rate risk factors for fixed income funding instruments are subject to the GIRR capital requirement. A relevant repo curve should be considered by currency.
The risk weights floored for interest rate and credit instruments is not permitted in the market risk standard when applying the risk weights for GIRR or for CSR, given that there is a possibility of the interest rates being negative (eg for JPY and EUR curves)
7.9 CSR non-securitisation risk factors
(1) Delta CSR non-securitisation: the CSR non-securitisation delta risk factors are defined along two dimensions:
(a) The relevant issuer credit spread curves (bond and CDS); and
(b) The following tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(2) Vega CSR non-securitisation: the vega risk factors are the implied volatilities of options that reference the relevant credit issuer names as underlyings (bond and CDS); further defined along one dimension - the maturity of the option. This is defined as the implied volatility of the option as mapped to one or several of the following maturity tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(3) Curvature CSR non-securitisation: the CSR non-securitisation curvature risk factors are defined along one dimension: the relevant issuer credit spread curves (bond and CDS). For instance, the bond-inferred spread curve of an issuer and the CDS-inferred spread curve of that same issuer should be considered a single spread curve. For the calculation of sensitivities, all tenors (as defined for CSR) are to be shifted in parallel.
For callable bonds, options on sovereign bond futures and bond options, the delta, vega and curvature capital requirements must be computed for both GIRR and CSR.
Bond and CDS credit spreads are considered distinct risk factors under [7.19](1), and pkɭ (basis) referenced in [7.54] and [7.55] is meant to capture only the bond-CDS basis.
7.10 CSR securitisation: non-CTP risk factors
(1) For securitisation instruments that do not meet the definition of CTP as set out in [6.5] (ie, non-CTP), the sensitivities of delta risk factors (ie CS01) must be calculated with respect to the spread of the tranche rather than the spread of the underlying of the instruments.
(2) Delta CSR securitisation (non-CTP): the CSR securitisation delta risk factors are defined along two dimensions:
(a) Tranche credit spread curves; and
(b) The following tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years to which delta risk factors are assigned.
(3) Vega CSR securitisation (non-CTP): Vega risk factors are the implied volatilities of options that reference non-CTP credit spreads as underlyings (bond and CDS); further defined along one dimension - the maturity of the option. This is defined as the implied volatility of the option as mapped to one or several of the following maturity tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(4) Curvature CSR securitisation (non-CTP): the CSR securitisation curvature risk factors are defined along one dimension, the relevant tranche credit spread curves (bond and CDS). For instance, the bond-inferred spread curve of a given Spanish residential mortgage- backed security (RMBS) tranche and the CDS-inferred spread curve of that given Spanish RMBS tranche would be considered a single spread curve. For the calculation of sensitivities, all the tenors are to be shifted in parallel.
7.11 CSR securitisation: CTP risk factors
(1) For securitisation instruments that meet the definition of a CTP as set out in [6.5], the sensitivities of delta risk factors (ie CS01) must be computed with respect to the names underlying the securitisation or nth-to-default instrument.
(2) Delta CSR securitisation (CTP): the CSR correlation trading delta risk factors are defined along two dimensions:
(a) The relevant underlying credit spread curves (bond and CDS); and
(b) The following tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years, to which delta risk factors are assigned.
(3) Vega CSR securitisation (CTP): the vega risk factors are the implied volatilities of options that reference CTP credit spreads as underlyings (bond and CDS), as defined along one dimension, the maturity of the option. This is defined as the implied volatility of the option as mapped to one or several of the following maturity tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(4) Curvature CSR securitisation (CTP): the CSR correlation trading curvature risk factors are defined along one dimension, the relevant underlying credit spread curves (bond and CDS). For instance, the bond-inferred spread curve of a given name within an iTraxx series and the CDS-inferred spread curve of that given underlying would be considered a single spread curve. For the calculation of sensitivities, all the tenors are to be shifted in parallel.
7.12 Equity risk factors
(1) Delta equity: the equity delta risk factors are:
(a) all the equity spot prices; and
(b) all the equity repurchase agreement rates (equity repo rates).
(2) Vega equity:
(a) The equity vega risk factors are the implied volatilities of options that reference the equity spot prices as underlyings as defined along one dimension, the maturity of the option. This is defined as the implied volatility of the option as mapped to one or several of the following maturity tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(b) There is no vega risk capital requirement for equity repo rates.
(3) Curvature equity:
(a) The equity curvature risk factors are all the equity spot prices.
(b) There is no curvature risk capital requirement for equity repo rates.
Repo rate risk factors for fixed income funding instruments are subject to the GIRR capital requirement. A relevant repo curve should be considered by currency.
7.13 Commodity risk factors
(1) Delta commodity: the commodity delta risk factors are all the commodity spot prices. However for some commodities such as electricity (which is defined to fall within bucket 3 (energy – electricity and carbon trading) in [7.82] the relevant risk factor can either be the spot or the forward price, as transactions relating to commodities such as electricity are more frequent on the forward price than transactions on the spot price. Commodity delta risk factors are defined along two dimensions:
(a) Legal terms with respect to the delivery location16 of the commodity; and
(b) Time to maturity of the traded instrument at the following tenors: 0 years, 0.25 years, 0.5 years, 1 year, 2 years, 3 years, 5 years, 10 years, 15 years, 20 years and 30 years.
(2) Vega commodity: the commodity vega risk factors are the implied volatilities of options that reference commodity spot prices as underlyings. No differentiation between commodity spot prices by the maturity of the underlying or delivery location is required. The commodity vega risk factors are further defined along one dimension, the maturity of the option. This is defined as the implied volatility of the option as mapped to one or several of the following maturity tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(3) Curvature commodity: the commodity curvature risk factors are defined along only one dimension, the constructed curve (ie no term structure decomposition) per commodity spot prices. For the calculation of sensitivities, all tenors (as defined for delta commodity) are to be shifted in parallel.
The current prices for futures and forward contracts should be used to compute the commodity delta risk factors. Commodity delta should be allocated to the relevant tenor based on the tenor of the futures and forward contract and given that spot commodity price positions should be slotted into the first tenor (0 years).
7.14 FX risk factors
(1) Delta FX: the FX delta risk factors are defined below.
(a) The FX delta risk factors are all the exchange rates between the currency in which an instrument is denominated and the reporting currency. For transactions that reference an exchange rate between a pair of non-reporting currencies, the FX delta risk factors are all the exchange rates between:
(i) the reporting currency; and
(ii) both the currency in which an instrument is denominated and any other currencies referenced by the instrument.17
(b) Subject to SAMA approval, FX risk may alternatively be calculated relative to a base currency instead of the reporting currency. In such case the bank must account for not only:
(i) the FX risk against the base currency; but also
(ii) the FX risk between the reporting currency and the base currency (ie translation risk).
(c) The resulting FX risk calculated relative to the base currency as set out in (b) is converted to the capital requirements in the reporting currency using the spot reporting/base exchange rate reflecting the FX risk between the base currency and the reporting currency.
(d) The FX base currency approach may be allowed under the following conditions:
(i) To use this alternative, a bank may only consider a single currency as its base currency; and
(ii) The bank shall demonstrate to SAMA that calculating FX risk relative to their proposed base currency provides an appropriate risk representation for their portfolio (for example, by demonstrating that it does not inappropriately reduce capital requirements relative to those that would be calculated without the base currency approach) and that the translation risk between the base currency and the reporting currency is taken into account.
(2) Vega FX: the FX vega risk factors are the implied volatilities of options that reference exchange rates between currency pairs; as defined along one dimension, the maturity of the option. This is defined as the implied volatility of the option as mapped to one or several of the following maturity tenors: 0.5 years, 1 year, 3 years, 5 years and 10 years.
(3) Curvature FX: the FX curvature risk factors are defined below.
(a) The FX curvature risk factors are all the exchange rates between the currency in which an instrument is denominated and the reporting currency. For transactions that reference an exchange rate between a pair of non-reporting currencies, the FX risk factors are all the exchange rates between:
(i) the reporting currency; and
(ii) both the currency in which an instrument is denominated and any other currencies referenced by the instrument.
(b) Where SAMA approval for the base currency approach has been granted for delta risks, FX curvature risks shall also be calculated relative to a base currency instead of the reporting currency, and then converted to the capital requirements in the reporting currency using the spot reporting/base exchange rate.
(4) No distinction is required between onshore and offshore variants of a currency for all FX delta, vega and curvature risk factors.
[7.14](4) states: “No distinction is required between onshore and offshore variants of a currency for all FX delta, vega and curvature risk factors.” This is also apply for deliverable/non-deliverable variants (eg KRO vs KRW, BRO vs BRL, INO vs INR)
Sensitivities-based method: definition of sensitivities
7.15 Sensitivities for each risk class must be expressed in the reporting currency of the bank.
7.16 For each risk factor defined in [7.8] to [7.14], sensitivities are calculated as the change in the market value of the instrument as a result of applying a specified shift to each risk factor, assuming all the other relevant risk factors are held at the current level as defined in [7.17] to [7.38].
As per [7.17], a bank may make use of alternative formulations of sensitivities based on pricing models that the bank’s independent risk control unit uses to report market risks or actual profits and losses to senior management. In doing so, the bank is to demonstrate to SAMA that the alternative formulations of sensitivities yield results very close to the prescribed formulations.
Requirements on instrument price or pricing models for sensitivity calculation
7.17 In calculating the risk capital requirement under the sensitivities-based method in [7], the bank must determine each delta and vega sensitivity and curvature scenario based on instrument prices or pricing models that an independent risk control unit within a bank uses to report market risks or actual profits and losses to senior management.
[7.17] states that banks must determine each delta sensitivity, vega sensitivity and curvature scenario based on instrument prices or pricing models that an independent risk control unit within a bank uses to report market risks or actual profits and losses to senior management. Banks should use zero rate or market rate sensitivities consistent with the pricing models referenced in that paragraph.
7.18 A key assumption of the standardised approach for market risk is that a bank’s pricing models used in actual profit and loss reporting provide an appropriate basis for the determination of regulatory capital requirements for all market risks. To ensure such adequacy, banks must at a minimum establish a framework for Prudent Valuation Guidance set out in Basel Framework .
Sensitivity definitions for delta risk
7.19 Delta GIRR: the sensitivity is defined as the PV01. PV01 is measured by changing the interest rate r at tenor t (rt) of the risk-free yield curve in a given currency by 1 basis point (ie 0.0001 in absolute terms) and dividing the resulting change in the market value of the instrument (Vi) by 0.0001 (ie 0.01%) as follows, where:
(1) rt is the risk-free yield curve at tenor t;
(2) cst is the credit spread curve at tenor t; and
(3) Vi is the market value of the instrument i as a function of the risk-free interest rate curve and credit spread curve:

7.20 Delta CSR non-securitisation, securitisation (non-CTP) and securitisation (CTP): the sensitivity is defined as CS01. The CS01 (sensitivity) of an instrument i is measured by changing a credit spread cs at tenor t (cst) by 1 basis point (ie 0.0001 in absolute terms) and dividing the resulting change in the market value of the instrument (Vi) by 0.0001 (ie 0.01%) as follows:
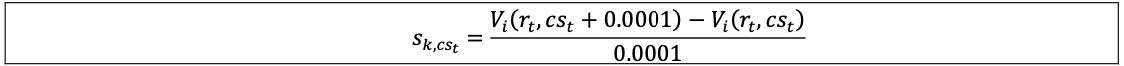
In cases where the bank does not have counterparty-specific money market curves, the bank can proxy PV01 to CS01
7.21 Delta equity spot: the sensitivity is measured by changing the equity spot price by 1 percentage point (ie 0.01 in relative terms) and dividing the resulting change in the market value of the instrument (Vi) by 0.01 (ie 1%) as follows, where:
(1) k is a given equity;
(2) EQk is the market value of equity k; and
(3) Vi is the market value of instrument i as a function of the price of equity k.

7.22 Delta equity repo rates: the sensitivity is measured by applying a parallel shift to the equity repo rate term structure by 1 basis point (ie 0.0001 in absolute terms) and dividing the resulting change in the market value of the instrument Vi by 0.0001 (ie 0.01%) as follows, where:
(1) k is a given equity;
(2) RTSk is the repo term structure of equity k; and
(3) Vi is the market value of instrument i as a function of the repo term structure of equity k.
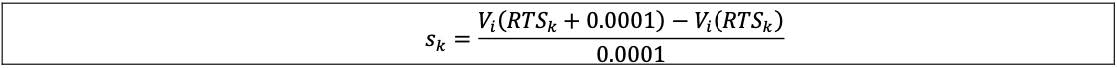
7.23 Delta commodity: the sensitivity is measured by changing the commodity spot price by 1 percentage point (ie 0.01 in relative terms) and dividing the resulting change in the market value of the instrument Vi by 0.01 (ie 1%) as follows, where:
(1) k is a given commodity;
(2) CTYk is the market value of commodity k; and
(3) Vi is the market value of instrument i as a function of the spot price of commodity k:
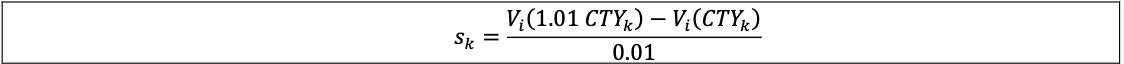
7.24 Delta FX: the sensitivity is measured by changing the exchange rate by 1 percentage point (ie 0.01 in relative terms) and dividing the resulting change in the market value of the instrument Vi by 0.01 (ie 1%), where:
(1) k is a given currency;
(2) FXk is the exchange rate between a given currency and a bank’s reporting currency or base currency, where the FX spot rate is the current market price of one unit of another currency expressed in the units of the bank’s reporting currency or base currency; and
(3) Vi is the market value of instrument i as a function of the exchange rate k:

Sensitivity definitions for vega risk
7.25 The option-level vega risk sensitivity to a given risk factor18 is measured by multiplying vega by the implied volatility of the option as follows, where:
(1) vega, ∂vi/∂σi, is defined as the change in the market value of the option Vi as a result of a small amount of change to the implied volatility σi, and
(2) the instrument’s vega and implied volatility used in the calculation of vega sensitivities must be sourced from pricing models used by the independent risk control unit of the bank.
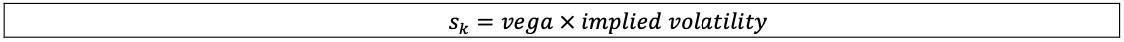
7.26 The following sets out how to derive vega risk sensitivities in specific cases:
(1) Options that do not have a maturity, are assigned to the longest prescribed maturity tenor, and these options are also assigned to the RRAO.
(2) Options that do not have a strike or barrier and options that have multiple strikes or barriers, are mapped to strikes and maturity used internally to price the option, and these options are also assigned to the RRAO.
(3) CTP securitisation tranches that do not have an implied volatility, are not subject to vega risk capital requirement. Such instruments may not, however, be exempt from delta and curvature risk capital requirements.
Under the sensitivities-based method and In the case where options do not have a specified maturity (eg cancellable swaps), the bank must assign those options to the longest prescribed maturity tenor for vega risk sensitivities and also assign such options to the RRAO.
In the case of the bank viewing the optionality of the cancellable swap as a swaption, the bank must assign the swaption to the longest prescribed maturity tenor for vega risk sensitivities (as it does not have a specified maturity) and derive the residual maturity of the underlying of the option accordingly.
Requirements on sensitivity computations
7.27 When computing a first-order sensitivity for instruments subject to optionality, banks should assume that the implied volatility either:
(1) remains constant, consistent with a “sticky strike” approach; or
(2) follows a “sticky delta” approach, such that implied volatility does not vary with respect to a given level of delta.
7.28 For the calculation of vega sensitivities, the distribution assumptions (ie log-normal assumptions or normal assumptions) for pricing models are applied as follows:
(1) For the computation of a vega GIRR or CSR sensitivity, banks may use either the log- normal or normal assumptions.
(2) For the computation of a vega equity, commodity or FX sensitivity, banks must use the log-normal assumption.19
To compute vega GIRR, banks may choose a mix of log-normal and normal assumptions for different currencies.
7.29 If, for internal risk management, a bank computes vega sensitivities using different definitions than the definitions set out in this standard, the bank may transform the sensitivities computed for internal risk management purposes to deduce the sensitivities to be used for the calculation of the vega risk measure.
7.30 All vega sensitivities must be computed ignoring the impact of credit valuation adjustments (CVA).
Treatment of index instruments and multi-underlying options
7.31 In the delta and curvature risk context: for index instruments and multi-underlying options, a look-through approach should be used. However, a bank may opt not to apply the look-through approach for instruments referencing any listed and widely recognised and accepted equity or credit index, where:
(1) it is possible to look-through the index (ie the constituents and their respective weightings are known);
(2) the index contains at least 20 constituents;
(3) no single constituent contained within the index represents more than 25% of the total index;
(4) the largest 10% of constituents represents less than 60% of the total index; and
(5) the total market capitalisation of all the constituents of the index is no less than USD 40 billion.
7.32 For a given instrument, irrespective of whether a look-through approach is adopted or not, the sensitivity inputs used for the delta and curvature risk calculation must be consistent.
7.33 Where a bank opts not to apply the look-through approach in accordance with [7.31], a single sensitivity shall be calculated to each widely recognised and accepted index that an instrument references. The sensitivity to the index should be assigned to the relevant delta risk bucket defined in [7.53] and [7.72] as follows:
(1) Where more than 75% of constituents in that index (taking into account the weightings of that index) would be mapped to a specific sector bucket (ie bucket 1 to bucket 11 for equity risk, or bucket 1 to bucket 16 for CSR), the sensitivity to the index shall be mapped to that single specific sector bucket and treated like any other single-name sensitivity in that bucket.
(2) In all other cases, the sensitivity may be mapped to an “index” bucket (ie bucket 12 or bucket 13 for equity risk; or bucket 17 or bucket 18 for CSR).
7.34 A look-through approach must always be used for indices that do not meet the criteria set out in [7.31](2) to [7.31](5), and for any multi-underlying instruments that reference a bespoke set of equities or credit positions.
(1) Where a look-through approach is adopted, for index instruments and multi-underlying options other than the CTP, the sensitivities to constituent risk factors from those instruments or options are allowed to net with sensitivities to single-name instruments without restriction.
(2) Index CTP instruments cannot be broken down into its constituents (ie the index CTP should be considered a risk factor as a whole) and the above-mentioned netting at the issuer level does not apply either.
(3) Where a look-through approach is adopted, it shall be applied consistently through time,20 and shall be used for all identical instruments that reference the same index.
Treatment of equity investments in funds
7.35 For equity investments in funds that can be looked through as set out in [5.8](5)(a), banks must apply a look-through approach and treat the underlying positions of the fund as if the positions were held directly by the bank (taking into account the bank’s share of the equity of the fund, and any leverage in the fund structure), except for the funds that meet the following conditions:
(1) For funds that hold an index instrument that meets the criteria set out under [7.31], banks must still apply a look-through and treat the underlying positions of the fund as if the positions were held directly by the bank, but the bank may then choose to apply the “no look-through” approach for the index holdings of the fund as set out in [7.33].
(2) For funds that track an index benchmark, a bank may opt not to apply the look-through approach and opt to measure the risk assuming the fund is a position in the tracked index only where:
(a) the fund has an absolute value of a tracking difference (ignoring fees and commissions) of less than 1%; and
(b) the tracking difference is checked at least annually and is defined as the annualised return difference between the fund and its tracked benchmark over the last 12 months of available data (or a shorter period in the absence of a full 12 months of data).
7.36 For equity investments in funds that cannot be looked through (ie do not meet the criterion set out in [5.8](5)(a)), but that the bank has access to daily price quotes and knowledge of the mandate of the fund (ie meet both the criteria set out in [5.8](5)(b)), banks may calculate capital requirements for the fund in one of three ways:
(1) If the fund tracks an index benchmark and meets the requirement set out in [7.35](2)(a) and (b), the bank may assume that the fund is a position in the tracked index, and may assign the sensitivity to the fund to relevant sector specific buckets or index buckets as set out in [7.33].
(2) Subject to SAMA approval, the bank may consider the fund as a hypothetical portfolio in which the fund invests to the maximum extent allowed under the fund’s mandate in those assets attracting the highest capital requirements under the sensitivities-based method, and then progressively in those other assets implying lower capital requirements. If more than one risk weight can be applied to a given exposure under the sensitivities-based method, the maximum risk weight applicable must be used.
(a) This hypothetical portfolio must be subject to market risk capital requirements on a stand-alone basis for all positions in that fund, separate from any other positions subject to market risk capital requirements.
(b) The counterparty credit and CVA risks of the derivatives of this hypothetical portfolio must be calculated using the simplified methodology set out in accordance with paragraph 80(vii)(c) of the banking book equity investment in funds treatment.
(3) A bank may treat their equity investment in the fund as an unrated equity exposure to be allocated to the “other sector” bucket (bucket 11). In applying this treatment, banks must also consider whether, given the mandate of the fund, the default risk capital (DRC) requirement risk weight prescribed to the fund is sufficiently prudent (as set out in [8.8]), and whether the RRAO should apply (as set out in [9.6]).
7.37 As per the requirement in [5.8](5), net long equity investments in a given fund in which the bank cannot look through or does not meet the requirements of [5.8](5) for the fund must be assigned to the banking book. Net short positions in funds, where the bank cannot look through or does not meet the requirements of [5.8](5), must be excluded from any trading book capital requirements under the market risk framework, with the net position instead subjected to a 100% capital requirement.
Treatment of vega risk for multi-underlying instruments
7.38 In the vega risk context:
(1) Multi-underlying options (including index options) are usually priced based on the implied volatility of the option, rather than the implied volatility of its underlying constituents and a look-through approach may not need to be applied, regardless of the approach applied to the delta and curvature risk calculation as set out in [7.31] through [6.35].21
(2) For indices, the vega risk with respect to the implied volatility of the multiunderlying options will be calculated using a sector specific bucket or an index bucket defined in [7.53] and [7.72] as follows:
(a) Where more than 75% of constituents in that index (taking into account the weightings of that index) would be mapped to a single specific sector bucket (ie bucket 1 to bucket 11 for equity risk; or bucket 1 to bucket 16 for CSR), the sensitivity to the index shall be mapped to that single specific sector bucket and treated like any other single-name sensitivity in that bucket.
(b) In all other cases, the sensitivity may be mapped to an “index” bucket (ie bucket 12 or bucket 13 for equity risk or bucket 17 or bucket 18 for CSR).
13 The assignment of risk factors to the specified tenors should be performed by linear interpolation or a method that is most consistent with the pricing functions used by the independent risk control function of a bank to report market risks or P&L to senior management.
14 Cross-currency basis are basis added to a yield curve in order to evaluate a swap for which the two legs are paid in two different currencies. They are in particular used by market participants to price cross-currency interest rate swaps paying a fixed or a floating leg in one currency, receiving a fixed or a floating leg in a second currency, and including an exchange of the notional in the two currencies at the start date and at the end date of the swap.
15 For example, an option with a forward starting cap, lasting 12 months, consists of four consecutive caplets on USD three month Libor. There are four (independent) options, with option expiry dates in 12, 15, 18 and 21 months. These options are all on underlying USD three-month Libor; the underlying always matures three months after the option expiry date (its residual maturity being three months). Therefore, the implied volatilities for a regular forward starting cap, which would start in one year and last for 12 months should be defined along the following two dimensions: (i) the maturity of the option’s individual components (caplets) – 12, 15, 18 and 21 months; and (ii) the residual maturity of the underlying of the option – three months.
16 For example, a contract that can be delivered in five ports can be considered having the same delivery location as another contract if and only if it can be delivered in the same five ports. However, it cannot be considered having the same delivery location as another contract that can be delivered in only four (or less) of those five ports.
17 For example, for an FX forward referencing USD/JPY, the relevant risk factors for a CAD- reporting bank to consider are the exchange rates USD/CAD and JPY/CAD. If that CAD- reporting bank calculates FX risk relative to a USD base currency, it would consider separate deltas for the exchange rate JPY/USD risk and CAD/USD FX translation risk and then translate the resulting capital requirement to CAD at the USD/CAD spot exchange rate.
18 As specified in the vega risk factor definitions in [7.8] to [7.14], the implied volatility of the option must be mapped to one or more maturity tenors.
19 Since vega (, ∂v/∂σi) of an instrument is multiplied by its implied volatility ( ), the vega risk sensitivity for that instrument will be the same under the log-normal assumption and the normal assumption. As a consequence, banks may use a log-normal or normal assumption for GIRR and CSR (in recognition of the trade-offs between constrained specification and computational burden for a standardised approach). For the other risk classes, banks must only use a log-normal assumption (in recognition that this is aligned with common practices across jurisdictions).
20 In other words, a bank can initially not apply a look-through approach, and later decide to apply it. However once applied (for a certain type of instrument referencing a particular index), the bank will require SAMA approval to revert to a “no look-through” approach.
21 As specified in the vega risk factor definitions in [7.8] to [7.14], the implied volatility of an option must be mapped to one or more maturity tenors.Sensitivities-Based Method: Definition of Delta Risk Buckets, Risk Weights and Correlations
7.39 [7.41] to [7.89] set out buckets, risk weights and correlation parameters for each risk class to calculate delta risk capital requirement as set out in [7.4].
7.40 The prescribed risk weights and correlations in [7.41] to [7.89] have been calibrated to the liquidity adjusted time horizon related to each risk class.
Delta GIRR buckets, risk weights and correlations
7.41 Each currency is a separate delta GIRR bucket, so all risk factors in risk-free yield curves for the same currency in which interest rate-sensitive instruments are denominated are grouped into the same bucket.
7.42 For calculating weighted sensitivities, the risk weights for each tenor in risk-free yield curves are set in Table 1 as follows:
Delta GIRR buckets and risk weights Table 1 Tenor 0.25 year 0.5 year 1 year 2 year 3 year Risk weight 1.7% 1.7% 1.6% 1.3% 1.2% Tenor 5 year 10 year 15 year 20 year 30 year Risk weight (percentage points) 1.1% 1.1% 1.1% 1.1% 1.1%
7.43
The risk weight for the inflation risk factor and the cross-currency basis risk factors, respectively, is set at 1.6%.
7.44 For specified currencies by the Basel Committee,22 the above risk weights may, at the discretion of the bank, be divided by the square root of 2.
7.45 For aggregating GIRR risk positions within a bucket, the correlation parameter ρkl between weighted sensitivities WSk and WSl within the same bucket (ie same currency), same assigned tenor, but different curves is set at 99.90%. In aggregating delta risk positions for cross-currency basis risk for onshore and offshore curves, which must be considered two different curves as set out in [7.8], a bank may choose to aggregate all cross-currency basis risk for a currency (ie “Curr/USD” or “Curr/EUR”) for both onshore and offshore curves by a simple sum of weighted sensitivities.
7.46 The delta risk correlation ρkl between weighted sensitivities WSk and WSl within the same bucket with different tenor and same curve is set in the following Table 2:23
Delta GIRR correlations (ρkl) within the same bucket, with different tenor and same curve Table 2 0.25 year 0.5 year 1 year 2 year 3 year 5 year 10 year 15 year 20 year 30 year 0.25 year 100.0% 97.0% 91.4% 81.1% 71.9% 56.6% 40.0% 40.0% 40.0% 40.0% 0.5 year 97.0% 100.0% 97.0% 91.4% 86.1% 76.3% 56.6% 41.9% 40.0% 40.0% 1 year 91.4% 97.0% 100.0% 97.0% 94.2% 88.7% 76.3% 65.7% 56.6% 41.9% 2 year 81.1% 91.4% 97.0% 100.0% 98.5% 95.6% 88.7% 82.3% 76.3% 65.7% 3 year 71.9% 86.1% 94.2% 98.5% 100.0% 98.0% 93.2% 88.7% 84.4% 76.3% 5 year 56.6% 76.3% 88.7% 95.6% 98.0% 100.0% 97.0% 94.2% 91.4% 86.1% 10 year 40.0% 56.6% 76.3% 88.7% 93.2% 97.0% 100.0% 98.5% 97.0% 94.2% 15 year 40.0% 41.9% 65.7% 82.3% 88.7% 94.2% 98.5% 100.0% 99.0% 97.0% 20 year 40.0% 40.0% 56.6% 76.3% 84.4% 91.4% 97.0% 99.0% 100.0% 98.5% 30 year 40.0% 40.0% 41.9% 65.7% 76.3% 86.1% 94.2% 97.0% 98.5% 100.0%
7.47
Between two weighted sensitivities WSk and WSl within the same bucket with different tenor and different curves, the correlation ρkl is equal to the correlation parameter specified in [7.46] multiplied by 99.90%.24
7.48 The delta risk correlation ρkl between a weighted sensitivity WSk to the inflation curve and a weighted sensitivity WSl to a given tenor of the relevant yield curve is 40%.
7.49 The delta risk correlation ρkl between a weighted sensitivity WSk to a cross-currency basis curve and a weighted sensitivity WSl to each of the following curves is 0%:
(1) a given tenor of the relevant yield curve;
(2) the inflation curve; or
(3) another cross-currency basis curve (if relevant).
7.50 For aggregating GIRR risk positions across different buckets (ie different currencies), the parameter γbc is set at 50%.
Delta CSR non-securitisations buckets, risk weights and correlations
7.51 For delta CSR non-securitisations, buckets are set along two dimensions – credit quality and sector – as set out in Table 3. The CSR non-securitisation sensitivities or risk exposures should first be assigned to a bucket defined before calculating weighted sensitivities by applying a risk weight.
Buckets for delta CSR non-securitisations Table 3 Bucket number Credit quality Sector 1 Investment grade (IG) Sovereigns including central banks, multilateral development banks 2 Local government, government-backed non-financials, education, public administration 3 Financials including government-backed financials 4 Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying 5 Consumer goods and services, transportation and storage, administrative and support service activities 6 Technology, telecommunications 7 Health care, utilities, professional and technical activities 8 Covered bonds25 9 High yield (HY) & non-rated (NR) Sovereigns including central banks, multilateral development banks 10 Local government, government-backed non-financials, education, public administration 11 Financials including government-backed financials 12 Basic materials, energy, industrials, agriculture, manufacturing, mining and quarrying 13 Consumer goods and services, transportation and storage, administrative and support service activities 14 Technology, telecommunications 15 Health care, utilities, professional and technical activities 16 Other sector26 17 IG indices 18 HY indices
Consistent with the treatment of external ratings under SAMA Minimum Capital Requirements for Credit Risk paragraphs 8.10 and 8.12, if there are two ratings which map into different risk weights, the higher risk weight should be applied. If there are three or more ratings with different risk weights, the ratings corresponding to the two lowest risk weights should be referred to and the higher of those two risk weights will be applied.
Consistent with the treatment where there are no external ratings, banks may, subject to SAMA approval:
- For the purpose of assigning delta CSR non-securitisation risk weights, map the internal rating to an external rating, and assign a risk weight corresponding to either “investment grade” or “high yield” in [7.51];
- For the purpose of assigning default risk weights under the DRC requirement, map the internal rating to an external rating, and assign a risk weight corresponding to one of the seven external ratings in the table included [8.24]; or
- Apply the risk weights specified in [7.51] and [8.24] for unrated/non-rated categories.
7.52 To assign a risk exposure to a sector, banks must rely on a classification that is commonly used in the market for grouping issuers by industry sector.
(1) The bank must assign each issuer to one and only one of the sector buckets in the table under [7.51].
(2) Risk positions from any issuer that a bank cannot assign to a sector in this fashion must be assigned to the other sector (ie bucket 16).
7.53 For calculating weighted sensitivities, the risk weights for buckets 1 to 18 are set out in Table 4. Risk weights are the same for all tenors (ie 0.5 years, 1 year, 3 years, 5 years, 10 years) within each bucket: Risk weights for buckets for delta CSR non-securitisations
Risk weights for buckets for delta CSR non-securitisations Table 4 Bucket number Risk weight 1 0.5% 2 1.0% 3 5.0% 4 3.0% 5 3.0% 6 2.0% 7 1.5% 8 2.5%27 9 2.0% 10 4.0% 11 12.0% 12 7.0% 13 8.5% 14 5.5% 15 5.0% 16 12.0% 17 1.5% 18 5.0%
7.54
For buckets 1 to 15, for aggregating delta CSR non-securitisations risk positions within a bucket, the correlation parameter ρkl between two weighted sensitivities WSk and WSɭ within the same bucket, is set as follows, where:
(1) ρkl (name) is equal to 1 where the two names of sensitivities k and ∫ are identical, and 35% otherwise;
(2) ρkl (tenor) is equal to 1 if the two tenors of the sensitivities k and ∫ are identical, and to 65% otherwise; and
(3) ρkl (basis) is equal to 1 if the two sensitivities are related to same curves, and 99.90% otherwise.
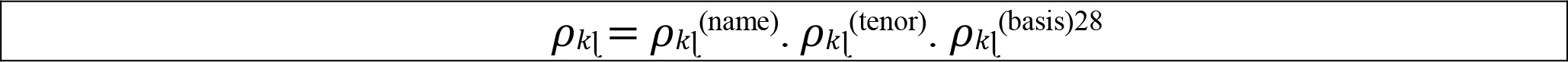
Bond and CDS credit spreads are considered distinct risk factors under [7.9](1), and ρkl(basis) referenced in [7.54] and [7.55] is meant to capture only the bond-CDS basis.
7.55 For buckets 17 and 18, for aggregating delta CSR non-securitisations risk positions within a bucket, the correlation parameter ρkl between two weighted sensitivities WSk and WSi within the same bucket is set as follows, where:
(1) ρk (name) is equal to 1 where the two names of sensitivities k and ∫ are identical, and 80% otherwise;
(2) ρk (tenor) is equal to 1 if the two tenors of the sensitivities k and ∫ are identical, and to 65% otherwise; and
(3) ρkl (basis) is equal to 1 if the two sensitivities are related to same curves, and 99.90%.
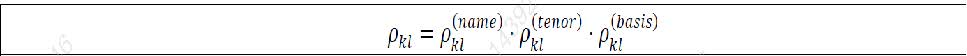
7.56 The correlations above do not apply to the other sector bucket (ie bucket 16).
(1) The aggregation of delta CSR non-securitisation risk positions within the other sector bucket (ie bucket 16) would be equal to the simple sum of the absolute values of the net weighted sensitivities allocated to this bucket. The same method applies to the aggregation of vega risk positions.
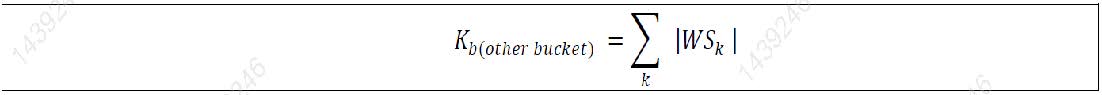
(2) The aggregation of curvature CSR non-securitisation risk positions within the other sector bucket (ie bucket 16) would be calculated by the formula below.
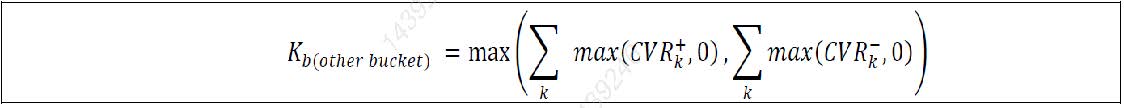
7.57 For aggregating delta CSR non-securitisation risk positions across buckets 1 to 16, the correlation parameter γbc is set as follows, where:
(1) γbc(rating) is equal to 50% where the two buckets b and c are both in buckets 1 to 15 and have a different rating category (either IG or HY/NR). γbc(rating) is equal to 1 otherwise; and
(2) γbc(sector) is equal to 1 if the two buckets belong to the same sector, and to the specified numbers in Table 5 otherwise.
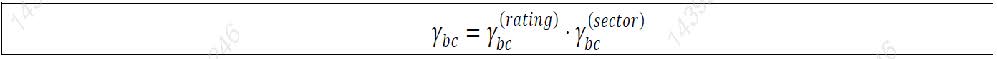
Values of γbc(sector) where the buckets do not belong to the same sector Table 5 Bucket 1/9 2/10 3/11 4/12 5/13 6/14 7/15 8 16 17 18 1/9 75% 10% 20% 25% 20% 15% 10% 0% 45% 45% 2/10 5% 15% 20% 15% 10% 10% 0% 45% 45% 3/11 5% 15% 20% 5% 20% 0% 45% 45% 4/12 20% 25% 5% 5% 0% 45% 45% 5/13 25% 5% 15% 0% 45% 45% 6/14 5% 20% 0% 45% 45% 7/15 5% 0% 45% 45% 8 0% 45% 45% 16 0% 0% 17 75% 18 Delta CSR securitisation (CTP) buckets, risk weights and correlations
7.58 Sensitivities to CSR arising from the CTP and its hedges are treated as a separate risk class as set out in 7.1]. The buckets, risk weights and correlations for the CSR securitisations (CTP) apply as follows:
(1) The same bucket structure and correlation structure apply to the CSR securitisations (CTP) as those for the CSR non-securitisation framework as set out in [7.51] to [7.57] with an exception of index buckets (ie buckets 17 and 18).
(2) The risk weights and correlation parameters of the delta CSR nonsecuritisations are modified to reflect longer liquidity horizons and larger basis risk as specified in [7.59] to [7.61].
7.59 For calculating weighted sensitivities, the risk weights for buckets 1 to 16 are set out in Table 6. Risk weights are the same for all tenors (ie 0.5 years, 1 year, 3 years, 5 years, 10 years) within each bucket:
Risk weights for sensitivities to CSR arising from the CTP Table 6 Bucket number Risk weight 1 4.0% 2 4.0% 3 8.0% 4 5.0% 5 4.0% 6 3.0% 7 2.0% 8 6.0% 9 13.0% 10 13.0% 11 16.0% 12 10.0% 13 12.0% 14 12.0% 15 12.0% 16 13.0%
7.60
For aggregating delta CSR securitisations (CTP) risk positions within a bucket, the delta risk correlation ρkl is derived the same way as in [7.54] and [7.55], except that the correlation parameter applying when the sensitivities are not related to same curves, ρkl (basis), is modified.
(1) ρkl (basis) is now equal to 1 if the two sensitivities are related to same curves, and 99.00% otherwise.
(2) The identical correlation parameters for ρkl(name) and ρkl(tenor) to CSR non-securitisation as set out in [7.54] and [7.55] apply.
7.61 For aggregating delta CSR securitisations (CTP) risk positions across buckets, the correlation parameters for γbc are identical to CSR non-securitisation as set out in [7.57].
Delta CSR securitisation (non-CTP) buckets, risk weights and correlations
7.62 For delta CSR securitisations not in the CTP, buckets are set along two dimensions– credit quality and sector – as set out in Table 7. The delta CSR securitisation (non-CTP) sensitivities or risk exposures must first be assigned to a bucket before calculating weighted sensitivities by applying a risk weight.
Buckets for delta CSR securitisations (non-CTP) Table 7 Bucket number Credit quality Sector 1 Senior investment grade (IG) RMBS – Prime 2 RMBS – Mid-prime 3 RMBS – Sub-prime 4 CMBS 5 Asset-backed securities (ABS) – Student loans 6 ABS – Credit cards 7 ABS – Auto 8 Collateralised loan obligation (CLO) non-CTP 9 Non-senior IG RMBS – Prime 10 RMBS – Mid-prime 11 RMBS – Sub-prime 12 Commercial mortgage-backed securities (CMBS) 13 ABS – Student loans 14 ABS – Credit cards 15 ABS – Auto 16 CLO non-CTP 17 High yield & non-rated RMBS – Prime 18 RMBS – Mid-prime 19 RMBS – Sub-prime 20 CMBS 21 ABS – Student loans 22 ABS – Credit cards 23 ABS – Auto 24 CLO non-CTP 25 Other Sector29
7.63
To assign a risk exposure to a sector, banks must rely on a classification that is commonly used in the market for grouping tranches by type.
(1) The bank must assign each tranche to one of the sector buckets in above Table 7.
(2) Risk positions from any tranche that a bank cannot assign to a sector in this fashion must be assigned to the other sector (ie bucket 25).
7.64 For calculating weighted sensitivities, the risk weights for buckets 1 to 8 (senior IG) are set out in Table 8:
Risk weights for buckets 1 to 8 for delta CSR securitisations (non-CTP) Table 8 Bucket number Risk weight (in percentage points) 1 0.9% 2 1.5% 3 2.0% 4 2.0% 5 0.8% 6 1.2% 7 1.2% 8 1.4%
7.65
The risk weights for buckets 9 to 16 (non-senior investment grade) are then equal to the corresponding risk weights for buckets 1 to 8 scaled up by a multiplication by 1.25. For instance, the risk weight for bucket 9 is equal to 1.25 × 0.9% = 1.125%.
7.66 The risk weights for buckets 17 to 24 (high yield and non-rated) are then equal to the corresponding risk weights for buckets 1 to 8 scaled up by a multiplication by 1.75. For instance, the risk weight for bucket 17 is equal to 1.75 × 0.9% = 1.575%.
7.67 The risk weight for bucket 25 is set at 3.5%.
7.68 For aggregating delta CSR securitisations (non-CTP) risk positions within a bucket, the correlation parameter ρkl between two sensitivities WSk and WSl within the same bucket, is set as follows, where:
(1) ρkl (tranche) is equal to 1 where the two names of sensitivities k and l are within the same bucket and related to the same securitisation tranche (more than 80% overlap in notional terms), and 40% otherwise;
(2) ρkl (tenor) is equal to 1 if the two tenors of the sensitivities k and l are identical, and to 80% otherwise; and
(3) ρkl (basis) is equal to 1 if the two sensitivities are related to same curves, and 99.90% otherwise.

[7.68] includes ρkl (tranche) , which equals 1 where the two sensitivities within the same bucket are related to the same securitisation tranche, or 40% otherwise. There is no issuer factor. This mean a two sensitivities relating to the same issuer but different tranches require 40% correlation. There is no granularity for issuers in the delta CSR securitisation part as set out in [7.10]. Where two tranches have exactly the same issuer, same tenor and same basis, but different tranches (ie different credit quality), the correlation must be 40%.
7.69 The correlations above do not apply to the other sector bucket (ie bucket 25).
(1) The aggregation of delta CSR securitisations (non-CTP) risk positions within the other sector bucket would be equal to the simple sum of the absolute values of the net weighted sensitivities allocated to this bucket. The same method applies to the aggregation of vega risk position.

(2) The aggregation of curvature CSR risk positions within the other sector bucket (ie bucket 16) would be calculated by the formula below.
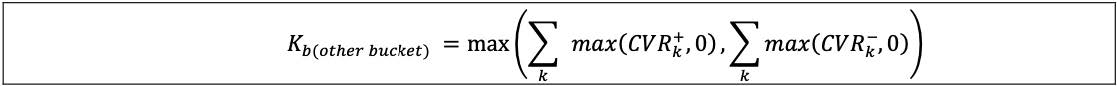
7.70 For aggregating delta CSR securitisations (non-CTP) risk positions across buckets 1 to 24, the correlation parameter γbc is set as 0%.
7.71 For aggregating delta CSR securitisations (non-CTP) risk positions between the other sector bucket (ie bucket 25) and buckets 1 to 24, the correlation parameter γbc is set at 1. Bucket level capital requirements will be simply summed up to the overall risk class level capital requirements, with no diversification or hedging effects recognised with any bucket.
Equity risk buckets, risk weights and correlations
7.72 For delta equity risk, buckets are set along three dimensions – market capitalisation, economy and sector – as set out in Table 9. The equity risk sensitivities or exposures must first be assigned to a bucket before calculating weighted sensitivities by applying a risk weight.
Buckets for delta sensitivities to equity risk Table 9 Bucket number Market cap Economy Sector 1 Large Emerging market economy Consumer goods and services, transportation and storage, administrative and support service activities, healthcare, utilities 2 Telecommunications, industrials 3 Basic materials, energy, agriculture, manufacturing, mining and quarrying 4 Financials including government-backed financials, real estate activities, technology 5 Advanced economy Consumer goods and services, transportation and storage, administrative and support service activities, healthcare, utilities 6 Telecommunications, industrials 7 Basic materials, energy, agriculture, manufacturing, mining and quarrying 8 Financials including government-backed financials, real estate activities, technology 9 Small Emerging market economy All sectors described under bucket numbers 1, 2, 3 and 4 10 Advanced economy All sectors described under bucket numbers 5, 6, 7 and 8 11 Other sector30 12 Large market cap, advanced economy equity indices (non-sector specific) 13 Other equity indices (non-sector specific)
7.73
Market capitalisation (market cap) is defined as the sum of the market capitalisations based on the market value of the total outstanding shares issued by the same listed legal entity or a group of legal entities across all stock markets globally, where the total outstanding shares issued by the group of legal entities refer to cases where the listed entity is a parent company of a group of legal entities. Under no circumstances should the sum of the market capitalisations of multiple related listed entities be used to determine whether a listed entity is “large market cap” or “small market cap”.
7.74 Large market cap is defined as a market capitalisation equal to or greater than USD 2 billion and small market cap is defined as a market capitalisation of less than USD 2 billion.
7.75 The advanced economies are Canada, the United States, Mexico, the euro area, the non-euro area western European countries (the United Kingdom, Norway, Sweden, Denmark and Switzerland), Japan, Oceania (Australia and New Zealand), Singapore and Hong Kong SAR.
An equity issuer must be allocated to a particular bucket according to the most material country or region in which the issuer operates. As stated in [7.76]: “For multinational multisector equity issuers, the allocation to a particular bucket must be done according to the most material region and sector in which the issuer operates.
7.76 To assign a risk exposure to a sector, banks must rely on a classification that is commonly used in the market for grouping issuers by industry sector.
(1) The bank must assign each issuer to one of the sector buckets in the table under [7.72] and it must assign all issuers from the same industry to the same sector.
(2) Risk positions from any issuer that a bank cannot assign to a sector in this fashion must be assigned to the other sector (ie bucket 11).
(3) For multinational multi-sector equity issuers, the allocation to a particular bucket must be done according to the most material region and sector in which the issuer operates.
7.77 For calculating weighted sensitivities, the risk weights for the sensitivities to each of equity spot price and equity repo rates for buckets 1 to 13 are set out in Table 10:
Risk weights for buckets 1 to 13 for sensitivities to equity risk Table 10 Bucket number Risk weight for equity spot price Risk weight for equity repo rate 1 55% 0.55% 2 60% 0.60% 3 45% 0.45% 4 55% 0.55% 5 30% 0.30% 6 35% 0.35% 7 40% 0.40% 8 50% 0.50% 9 70% 0.70% 10 50% 0.50% 11 70% 0.70% 12 15% 0.15% 13 25% 0.25%
7.78
For aggregating delta equity risk positions within a bucket, the correlation parameter ρkl between two sensitivities WSk and WSl within the same bucket is set at as follows
(1) The correlation parameter ρkl is set at 99.90%, where:
(a) one is a sensitivity to an equity spot price and the other a sensitivity to an equity repo rates; and
(b) both are related to the same equity issuer name.
(2) The correlation parameter ρkl is set out in (a) to (d) below, where both sensitivities are to equity spot price, and where:
(a) 15% between two sensitivities within the same bucket that fall under large market cap, emerging market economy (bucket number 1, 2, 3 or 4).
(b) 25% between two sensitivities within the same bucket that fall under large market cap, advanced economy (bucket number 5, 6, 7 or 8).
(c) 7.5% between two sensitivities within the same bucket that fall under small market cap, emerging market economy (bucket number 9).
(d) 12.5% between two sensitivities within the same bucket that fall under small market cap, advanced economy (bucket number 10).
(e) 80% between two sensitivities within the same bucket that fall under either index bucket (bucket number 12 or 13)
(3) The same correlation parameter ρkl as set out in above (2)(a) to (d) apply, where both sensitivities are to equity repo rates.
(4) The correlation parameter ρkl is set as each parameter specified in above (2)(a) to (d) multiplied by 99.90%, where:
(a) One is a sensitivity to an equity spot price and the other a sensitivity to an equity repo rate; and
(b) Each sensitivity is related to a different equity issuer name.
7.79 The correlations set out above do not apply to the other sector bucket (ie bucket 11).
(1) The aggregation of equity risk positions within the other sector bucket capital requirement would be equal to the simple sum of the absolute values of the net weighted sensitivities allocated to this bucket. The same method applies to the aggregation of vega risk positions.

(2) The aggregation of curvature equity risk positions within the other sector bucket (ie bucket 11) would be calculated by the formula:
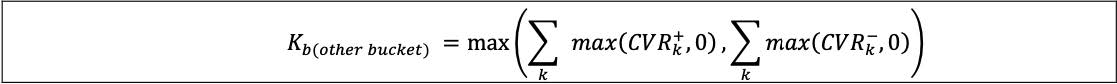
7.80 For aggregating delta equity risk positions across buckets 1 to 13, the correlation parameter γbc is set at:
(1) 15% if bucket b and bucket c fall within bucket numbers 1 to 10;
(2) 0% if either of bucket b and bucket c is bucket 11;
(3) 75% if bucket b and bucket c are bucket numbers 12 and 13 (i.e. one is bucket 12, one is bucket 13); and
(4) 45% otherwise.
Commodity risk buckets, risk weights and correlations
7.81 For delta commodity risk, 11 buckets that group commodities by common characteristics are set out in Table 11.
7.82 For calculating weighted sensitivities, the risk weights for each bucket are set out in Table 11:
Delta commodity buckets and risk weights Table 11 Bucket number Commodity bucket Examples of commodities allocated to each commodity bucket (non-exhaustive) Risk weight 1 Energy - solid combustibles Coal, charcoal, wood pellets, uranium 30% 2 Energy - liquid combustibles Light-sweet crude oil; heavy crude oil; West Texas Intermediate (WTI) crude; Brent crude; etc (ie various types of crude oil)
Bioethanol; biodiesel; etc (ie various biofuels)
Propane; ethane; gasoline; methanol; butane; etc (ie various petrochemicals)
Jet fuel; kerosene; gasoil; fuel oil; naphtha; heating oil; diesel etc (ie various refined fuels)35% 3 Energy - electricity and carbon trading Spot electricity; day-ahead electricity; peak electricity; off-peak electricity (ie various electricity types)
Certified emissions reductions; in-delivery month EU allowance; Regional Greenhouse Gas Initiative CO2 allowance; renewable energy certificates; etc (ie various carbon trading emissions)60% 4 Freight Capesize; Panamax; Handysize; Supramax (ie various types of dry-bulk route)
Suezmax; Aframax; very large crude carriers (ie various liquid-bulk/gas shipping route)80% 5 Metals — non-precious Aluminium; copper; lead; nickel; tin; zinc (ie various base metals)
Steel billet; steel wire; steel coil; steel scrap; steel rebar; iron ore; tungsten; vanadium; titanium; tantalum (ie steel raw materials)
Cobalt; manganese; molybdenum (ie various minor metals)40% 6 Gaseous combustibles Natural gas; liquefied natural gas 45% 7 Precious metals (including gold) Gold; silver; platinum; palladium 20% 8 Grains and oilseed Corn; wheat; soybean seed; soybean oil; soybean meal; oats; palm oil; canola; barley; rapeseed seed; rapeseed oil; rapeseed meal; red bean; sorghum; coconut oil; olive oil; peanut oil; sunflower oil; rice 35% 9 Livestock and dairy Live cattle; feeder cattle; hog; poultry; lamb; fish; shrimp; milk; whey; eggs; butter; cheese 25% 10 Softs and other agriculturals Cocoa; arabica coffee; robusta coffee; tea; citrus juice; orange juice; potatoes; sugar; cotton; wool; lumber;pulp; rubber 35% 11 Other commodity Potash; fertilizer; phosphate rocks (ie various industrial materials)
Rare earths; terephthalic acid; flat glass50%
7.83
For the purpose of aggregating commodity risk positions within a bucket using a correlation parameter, the correlation parameter ρkl between two sensitivities WSk and WSl within the same bucket, is set as follows, where:
(1) ρkl(cty) is equal to 1 where the two commodities of sensitivities k and l are identical, and to the intra-bucket correlations in Table 12 otherwise, where, any two commodities are considered distinct commodities if in the market two contracts are considered distinct when the only difference between each other is the underlying commodity to be delivered. For example, WTI and Brent in bucket 2 (ie energy – liquid combustibles) would typically be treated as distinct commodities;
(2) ρkl(tenor) is equal to 1 if the two tenors of the sensitivities k and l are identical, and to 99.00% otherwise; and
(3) ρkl(basis) is equal to 1 if the two sensitivities are identical in the delivery location of a commodity, and 99.90% otherwise.
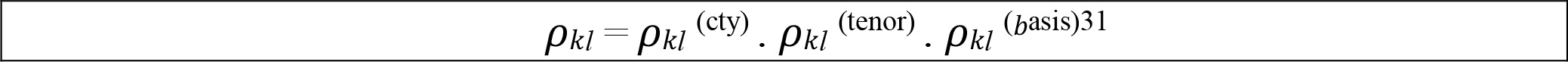
Values of ρkl(cty) for intra-bucket correlations Table 12 Bucket number Commodity bucket Correlation ρkl(cty) 1 Energy - Solid combustibles 55% 2 Energy - Liquid combustibles 95% 3 Energy - Electricity and carbon trading 40% 4 Freight 80% 5 Metals - non-precious 60% 6 Gaseous combustibles 65% 7 Precious metals (including gold) 55% 8 Grains and oilseed 45% 9 Livestock and dairy 15% 10 Softs and other agriculturals 40% 11 Other commodity 15%
Instruments with a spread as their underlying are considered sensitive to different risk factors. In the example cited, the swap will be sensitive to both WTI and Brent, each of which require a capital charge at the risk factor level (ie delta of WTI and delta of Brent). The correlation to aggregate capital charges is specified in [7.83].
7.84 For determining whether the commodity correlation parameter (ρkl(cty)) as set out in Table 12 in [7.83](1)(a) should apply, this paragraph provides non-exhaustive examples of further definitions of distinct commodities as follows:
(1) For bucket 3 (energy – electricity and carbon trading):
(a) Each time interval (i) at which the electricity can be delivered and (ii) that is specified in a contract that is made on a financial market is considered a distinct electricity commodity (eg peak and off-peak).
(b) Electricity produced in a specific region (eg Electricity NE, Electricity SE or Electricity North) is considered a distinct electricity commodity.
(2) For bucket 4 (freight):
(a) Each combination of freight type and route is considered a distinct commodity.
(b) Each week at which a good has to be delivered is considered a distinct commodity.
7.85 For aggregating delta commodity risk positions across buckets, the correlation parameter ybc is set as follows:
(1) 20% if bucket b and bucket c fall within bucket numbers 1 to 10; and
(2) 0% if either bucket b or bucket c is bucket number 11.
Foreign exchange risk buckets, risk weights and correlations
7.86 An FX risk bucket is set for each exchange rate between the currency in which an instrument is denominated and the reporting currency.
7.87 A unique relative risk weight equal to 15% applies to all the FX sensitivities.
7.88 For specified currency pairs,32 and for currency pairs forming first- order crosses across these specified currency pairs,33 the above risk weight may at the discretion of the bank be divided by the square root of 2.
7.89 For aggregating delta FX risk positions across buckets, the correlation parameter Ybc is uniformly set to 60%.
22 Specified currencies by the Basel Committee are: EUR, USD, GBP, AUD, JPY, SEK, CAD as well as the domestic reporting currency of a bank.
23 The delta GIRR correlation parameters (ρkl) set out in Table 2 is determined by ma , where Tk (respectivelyTl) is the tenor that relates to WSk (respectively WSl); and θ is set at 3%. For example, the correlation between a sensitivity to the one-year tenor of the Eonia swap curve and the a sensitivity to the five-year tenor of the Eonia swap curve in the same currency is max
, where Tk (respectivelyTl) is the tenor that relates to WSk (respectively WSl); and θ is set at 3%. For example, the correlation between a sensitivity to the one-year tenor of the Eonia swap curve and the a sensitivity to the five-year tenor of the Eonia swap curve in the same currency is max 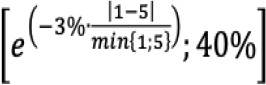 = 88.69%
= 88.69%
24 For example, the correlation between a sensitivity to the one-year tenor of the Eonia swap curve and a sensitivity to the five-year tenor of the three-month Euribor swap curve in the same currency is (88.69%) . (0.999) = 88.60%.
25 Covered bonds must meet the definition provided by Large Exposure Rules for Banks issued via SAMA circular No. 1651 / 67 dated 09/01/1441.
26 Credit quality is not a differentiating consideration for this bucket.
27 For covered bonds that are rated AA- or higher, the applicable risk weight may at the discretion of the bank be 1.5%..
28 For example, a sensitivity to the five-year Apple bond curve and a sensitivity to the 10- year Google CDS curve would be 35% . .65% . 99.90% = 22.73%.
29 Credit quality is not a differentiating consideration for this bucket.
30 Market capitalisation or economy (ie advanced or emerging market) is not a differentiating consideration for this bucket.
31 For example, the correlation between the sensitivity to Brent, one-year tenor, for delivery in Le Havre and the sensitivity to WTI, five-year tenor, for delivery in Oklahoma is 95% - 99.00% - 99.90% = 93.96%.
32 Specified currency pairs are: SAR/USD, USD/EUR, USD/JPY, USD/GBP, USD/AUD, USD/CAD, USD/CHF, USD/MXN, USD/CNY, USD/NZD, USD/RUB, USD/HKD, USD/SGD, USD/TRY, USD/KRW, USD/SEK, USD/ZAR, USD/INR, USD/NOK, USD/BRL.
33 example, EUR/AUD is not among the selected currency pairs specified by the Basel Committee, but is a first-order cross of USD/EUR and USD/AUD.Sensitivities-Based Method: Definition of Vega Risk Buckets, Risk Weights and Correlations
7.90 [7.91] to [7.95] set out buckets, risk weights and correlation parameters to calculate vega risk capital requirement as set out in [7.4].
7.91 The same bucket definitions for each risk class are used for vega risk as for delta risk.
7.92 For calculating weighted sensitivities for vega risk, the risk of market illiquidity is incorporated into the determination of vega risk, by assigning different liquidity horizons for each risk class as set out in Table 13. The risk weight for each risk class34 is also set out in Table 13.
Regulatory liquidity horizon, LHrisk class and risk weights per risk class Table 13 Risk class LHrisk class Risk weights GIRR 60 100% CSR non-securitisations 120 100% CSR securitisations (CTP) 120 100% CSR securitisations (non-CTP) 120 100% Equity (large cap and indices) 20 77.78% Equity (small cap and other sector) 60 100% Commodity 120 100% FX 40 100%
7.93
For aggregating vega GIRR risk positions within a bucket, the correlation parameter ρkl is set as follows, where:
(1) pkl (option maturity) is equal to ? 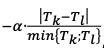 , where:
, where:
(a) α is set at 1%;
(b) Tk (respectively Tl) is the maturity of the option from which the vega sensitivity VRk (VRl) is derived, expressed as a number of years; and
(2) pkl(underlyins maturity) is equal to ? 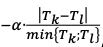 , where:
, where:
(a) α is set at 1%; and
(b) Tku (respectively Tlu) is the maturity of the underlying of the option from which the sensitivity VRk (VRl) is derived, expressed as a number of years after the maturity of the option.

7.95 For aggregating vega risk positions across different buckets within a risk class (GIRR and non- GIRR), the same correlation parameters for γbc, as specified for delta correlations for each risk class in [7.39] to [7.89] are to be used for the aggregation of vega risk (eg γbc = 50% is to be used for the aggregation of vega risk sensitivities across different GIRR buckets).
34 risk weight for a given vega risk factor k (RWk) is determined by RWk = min
 , where RW∂ is set at 55%; and LHrisk class is specified per risk class in Table 13.
, where RW∂ is set at 55%; and LHrisk class is specified per risk class in Table 13.Sensitivities-Based Method: Definition of Curvature Risk Buckets, Risk Weights and Correlations
7.96 [7.97] to [7.101] set out buckets, risk weights and correlation parameters to calculate curvature risk capital requirement as set out in [7.5].
7.97 The delta buckets are replicated for the calculation of curvature risk capital requirement, unless specified otherwise in the preceding paragraphs within [7.8] to [7.89].
7.98 For calculating the net curvature risk capital requirement CVRk for risk factor k for FX and equity risk classes, the curvature risk weight, which is the size of a shock to the given risk factor, is a relative shift equal to the respective delta risk weight. For FX curvature, for options that do not reference a bank’s reporting currency (or base currency as set out in [7.14](b)) as an underlying, net curvature risk charges (CVRk+ and CVRk- ) may be divided by a scalar of 1.5. Alternatively, and subject to SAMA approval, a bank may apply the scalar of 1.5 consistently to all FX instruments provided curvature sensitivities are calculated for all currencies, including sensitivities determined by shocking the reporting currency (or base currency where used) relative to all other currencies.
7.99 For calculating the net curvature risk capital requirement CVRk for curvature risk factor k for GIRR, CSR and commodity risk classes, the curvature risk weight is the parallel shift of all the tenors for each curve based on the highest prescribed delta risk weight for each risk class. For example, in the case of GIRR the risk weight assigned to 0.25-year tenor (ie the most punitive tenor risk weight) is applied to all the tenors simultaneously for each risk-free yield curve (consistent with a “translation”, or “parallel shift” risk calculation).
7.100 For aggregating curvature risk positions within a bucket, the curvature risk correlations pkl are determined by squaring the corresponding delta correlation parameters pkl except for CSR non-securitisations and CSR securitisations (CTP). In applying the high and low correlations scenario set out in [7.6], the curvature risk capital requirements are calculated by applying the curvature correlation parameters pkl determined in this paragraph.
(1) For CSR non-securitisations and CSR securitisations (CTP), consistent with [7.9] which defines a bucket along one dimension (ie the relevant credit spread curve), the correlation parameter pkl as defined in [7.54] and [7.55] is not applicable to the curvature risk capital requirement calculation. Thus, the correlation parameter is determined by whether the two names of weighted sensitivities are the same. In the formula in [7.54] and [7.55], the correlation parameters pkl(basis) and pkl(tenor) need not apply and only correlation parameter pkl (name) applies between two weighted sensitivities within the same bucket. This correlation parameter should be squared.
[7.100] states that, for curvature risk of CSR non-securitisation, the correlation parameters pkl(basis) and pkl(tenor) need not apply and only correlation parameter pkl(name) applies between two sensitivities WSk and WSl within the same bucket.
7.101 For aggregating curvature risk positions across buckets, the curvature risk correlations γbc are determined by squaring the corresponding delta correlation parameters γbc. For instance, when aggregating C VREUR and CVRUSD for the GIRR, the correlation should be 50%2 = 25% . In applying the high and low correlations scenario set out in [7.6], the curvature risk capital requirements are calculated by applying the curvature correlation parameters γbc, (ie the square of the corresponding delta correlation parameter).

