6. Standardized Approach to Counterparty Credit Risk
Overview and Scope
6.1. The Standardized Approach for Counterparty Credit Risk (SA-CCR) applies to over the-counter (OTC) derivatives, exchange-traded derivatives and long settlement transactions.5 Banks that do not have approval to apply the internal model method (IMM) for the relevant transactions must use SA-CCR, as set out in this chapter.
6.2. EAD is to be calculated separately for each netting set (as set out in 4.14 , each transaction that is not subject to a legally enforceable bilateral netting arrangement that is recognized for regulatory capital purposes should be interpreted as its own netting set).6 It is determined using the following formula, where:
(1) alpha = 1.4
(2) RC = the replacement cost calculated according to 6.5 to 6.21
(3) PFE = the amount for potential future exposure calculated according to 6.22 to 6.79
EAD = alpha * (RC + PFE)
6.3. For credit derivatives where the bank is the protection seller and that are outside netting and margin agreements, the EAD may be capped to the amount of unpaid premia. Banks have the option to remove such credit derivatives from their legal netting sets and treat them as individual unmargined transactions in order to apply the cap.
6.4. The replacement cost (RC) and the potential future exposure (PFE) components are calculated differently for margined and unmargined netting sets. Margined netting sets are netting sets covered by a margin agreement under which the bank’s counterparty has to post variation margin; all other netting sets, including those covered by a one-way margin agreement where only the bank posts variation margin, are treated as unmargined for the purposes of the SA-CCR. The EAD for a margined netting set is capped at the EAD of the same netting set calculated on an unmargined basis.
5 See chapter 12 and Chapter 13 of this framework for illustrative examples of the application of the SA-CCR to sample portfolios
6 The EAD can be set to zero only for sold options that are outside netting and margin agreements.Replacement Cost and Net Independent Collateral Amount
6.5. For unmargined transactions, the RC intends to capture the loss that would occur if a counterparty were to default and were closed out of its transactions immediately. The PFE add-on represents a potential conservative increase in exposure over a one-year time horizon from the present date (i.e. the calculation date).
6.6. For margined trades, the RC intends to capture the loss that would occur if a counterparty were to default at the present or at a future time, assuming that the closeout and replacement of transactions occur instantaneously. However, there may be a period (the margin period of risk) between the last exchange of collateral before default and replacement of the trades in the market. The PFE add-on represents the potential change in value of the trades during this time period.
6.7. In both cases, the haircut applicable to noncash collateral in the replacement cost formulation represents the potential change in value of the collateral during the appropriate time period (one year for unmargined trades and the margin period of risk for margined trades).
6.8. Replacement cost is calculated at the netting set level, whereas PFE add-ons are calculated for each asset class within a given netting set and then aggregated (see 6.26 to 6.79 below).
6.9. For capital adequacy purposes, banks may net transactions (e.g. when determining the RC component of a netting set) subject to novation under which any obligation between a bank and its counterparty to deliver a given currency on a given value date is automatically amalgamated with all other obligations for the same currency and value date, legally substituting one single amount for the previous gross obligations. Banks may also net transactions subject to any legally valid form of bilateral netting not covered in the preceding sentence, including other forms of novation. In every such case where netting is applied, a bank must satisfy SAMA that it has:
(1) A netting contract with the counterparty or other agreement which creates a single legal obligation, covering all included transactions, such that the bank would have either a claim to receive or obligation to pay only the net sum of the positive and negative mark-to-market values of included individual transactions in the event a counterparty fails to perform due to any of the following: default, bankruptcy, liquidation or similar circumstances.7
(2) Written and reasoned legal reviews that, in the event of a legal challenge, the relevant courts and administrative authorities would find the bank’s exposure to be such a net amount under:
(3) The law of the jurisdiction in which the counterparty is chartered and, if the foreign branch of a counterparty is involved, then also under the law of the jurisdiction in which the branch is located;
(a) The law that governs the individual transactions; and
(b) The law that governs any contract or agreement necessary to effect the netting.
(4) Procedures in place to ensure that the legal characteristics of netting arrangements are kept under review in light of the possible changes in relevant law.
6.10. SAMA, after consultation when necessary with other relevant supervisors, must be satisfied that the netting is enforceable under the laws of each of the relevant jurisdictions. Thus, if any of these supervisors is dissatisfied about enforceability under its laws, the netting contract or agreement will not meet this condition and neither counterparty could obtain supervisory benefit.
6.11. There are two formulations of replacement cost depending on whether the trades with a counterparty are margined or unmargined. The margined formulation could apply both to bilateral transactions and to central clearing relationships. The formulation also addresses the various arrangements that a bank may have to post and/or receive collateral that may be referred to as initial margin.
Formulation for unmargined transactions
6.12. For unmargined transactions, RC is defined as the greater of:
(i) the current market value of the derivative contracts less net haircut collateral held by the bank (if any), and
(ii) zero. This is consistent with the use of replacement cost as the measure of current exposure, meaning that when the bank owes the counterparty money it has no exposure to the counterparty if it can instantly replace its trades and sell collateral at current market prices.8
The formula for RC is as follows, where:
(1) V is the value of the derivative transactions in the netting set
(2) C is the haircut value of net collateral held, which is calculated in accordance with the net independent collateral amount (NICA) methodology defined in 6.19.9
RC = max{V - C; 0}
6.13. For the purpose of 6.12 above, the value of non-cash collateral posted by the bank to its counterparty is increased and the value of the non-cash collateral received by the bank from its counterparty is decreased using haircuts (which are the same as those that apply to repo-style transactions) for the time periods described in 6.7above.
6.14. The formulation set out in 6.12 above, does not permit the replacement cost, which represents today’s exposure to the counterparty, to be less than zero. However, banks sometimes hold excess collateral (even in the absence of a margin agreement) or have out-of-the-money trades which can further protect the bank from the increase of the exposure. As discussed in 6.23 to 6.25 below, the SA-CCR allows such over-collateralization and negative mark-to market value to reduce PFE, but they are not permitted to reduce replacement cost.
Formulation for margined transactions
6.15. The RC formula for margined transactions builds on the RC formula for unmargined transactions. It also employs concepts used in standard margining agreements, as discussed more fully below.
6.16. The RC for margined transactions in the SA-CCR is defined as the greatest exposure that would not trigger a call for VM, taking into account the mechanics of collateral exchanges in margining agreements.10 Such mechanics include, for example, “Threshold”, “Minimum Transfer Amount” and “Independent Amount” in the standard industry documentation,11 which are factored into a call for VM.12 A defined, generic formulation has been created to reflect the variety of margining approaches used and those being considered by supervisors internationally.
Incorporating NICA into replacement cost
6.17. One objective of the SA-CCR is to reflect the effect of margining agreements and the associated exchange of collateral in the calculation of CCR exposures. The following paragraphs address how the exchange of collateral is incorporated into the SA-CCR.
6.18. To avoid confusion surrounding the use of terms initial margin and independent amount which are used in various contexts and sometimes interchangeably, the term independent collateral amount (ICA) is introduced. ICA represents:
(i) collateral (other than VM) posted by the counterparty that the bank may seize upon default of the counterparty, the amount of which does not change in response to the value of the transactions it secures and/or
(ii) the Independent Amount (IA) parameter as defined in standard industry documentation. ICA can change in response to factors such as the value of the collateral or a change in the number of transactions in the netting set.
6.19. Because both a bank and its counterparty may be required to post ICA, it is necessary to introduce a companion term, net independent collateral amount (NICA), to describe the amount of collateral that a bank may use to offset its exposure on the default of the counterparty. NICA does not include collateral that a bank has posted to a segregated, bankruptcy remote account, which presumably would be returned upon the bankruptcy of the counterparty. That is, NICA represents any collateral (segregated or unsegregated) posted by the counterparty less the unsegregated collateral posted by the bank. With respect to IA, NICA takes into account the differential of IA required for the bank minus IA required for the counterparty.
6.20. For margined trades, the replacement cost is calculated using the following formula, where:
(1) V and C are defined as in the unmargined formulation, except that C now includes the net variation margin amount, where the amount received by the bank is accounted with a positive sign and the amount posted by the bank is accounted with a negative sign
(2) TH is the positive threshold before the counterparty must send the bank collateral
(3) MTA is the minimum transfer amount applicable to the counterparty
RC = max{V - C; TH + MTA - NICA; 0}
6.21. TH + MTA – NICA represents the largest exposure that would not trigger a VM call and it contains levels of collateral that need always to be maintained. For example, without initial margin or IA, the greatest exposure that would not trigger a variation margin call is the threshold plus any minimum transfer amount. In the adapted formulation, NICA is subtracted from TH + MTA. This makes the calculation more accurate by fully reflecting both the actual level of exposure that would not trigger a margin call and the effect of collateral held and /or posted by a bank. The calculation is floored at zero, recognizing that the bank may hold NICA in excess of TH + MTA, which could otherwise result in a negative replacement cost.
PFE add-on for each netting set
6.22. The PFE add-on consists of:
(i) an aggregate add-on component; and
(ii) a multiplier that allows for the recognition of excess collateral or negative mark-to-market value for the transactions within the netting set. The formula for PFE is as follows, where:
(1) AddOnaggregate is the aggregate add-on component (see 6.27 below)
(2) multiplier is defined as a function of three inputs: V, C and AddOnaggregate
PFE = multiplier * AddOnaggregate
7 The netting contract must not contain any clause which, in the event of default of a counterparty, permits a non-defaulting counterparty to make limited payments only, or no payments at all, to the estate of the defaulting party, even if the defaulting party is a net creditor.
8 The haircut applicable in the replacement cost calculation for unmargined trades should follow the formula in paragraphs 62 of chapter 9 of the Minimum Capital Requirements for Credit Risk. In applying the formula, banks must use the maturity of the longest transaction in the netting set as the value for N , capped at 250 days, in order to R scale haircuts for unmargined trades, which is capped at 100%.
9 As set out in 6.4, netting sets that include a one-way margin agreement in favor of the bank’s counterparty (i.e. the bank posts, but does not receive variation margin) are treated as unmargined for the purposes of SA-CCR. For such netting sets, C also includes, with a negative sign, the variation margin amount posted by the bank to the counterparty.
10 See chapter 12 and Chapter 13 of this framework for illustrative examples of the effect of standard margin agreements on the SA-CCR formulation.
11 For example, the 1992 (Multicurrency-Cross Border) Master Agreement and the 2002 Master Agreement published by the International Swaps & Derivatives Association, Inc. (ISDA Master Agreement). The ISDA Master Agreement includes the ISDA Credit Support Annexes: the 1994 Credit Support Annex (Security Interest – New York Law), or, as applicable, the 1995 Credit Support Annex (Transfer – English Law) and the 1995 Credit Support Deed (Security Interest – English Law).
12 For example, in the ISDA Master Agreement, the term “Credit Support Amount”, or the overall amount of collateral that must be delivered between the parties, is defined as the greater of the Secured Party’s Exposure plus the aggregate of all Independent Amounts applicable to the Pledgor minus all Independent Amounts applicable to the Secured Party, minus the Pledgor’s Threshold and zero.Multiplier (Recognition of Excess Collateral and Negative Mark-to-Market)
6.23. As a general principle, over-collateralization should reduce capital requirements for counterparty credit risk. In fact, many banks hold excess collateral (i.e. collateral greater than the net market value of the derivatives contracts) precisely to offset potential increases in exposure represented by the add-on. As discussed in 6.12 and 6.20, collateral may reduce the replacement cost component of the exposure under the SA-CCR. The PFE component also reflects the risk-reducing property of excess collateral.
6.24. Banks should apply a multiplier to the PFE component that decreases as excess collateral increases, without reaching zero (the multiplier is floored at 5% of the PFE add-on). When the collateral held is less than the net market value of the derivative contracts (“under-collateralization”), the current replacement cost is positive and the multiplier is equal to one (i.e. the PFE component is equal to the full value of the aggregate add-on). Where the collateral held is greater than the net market value of the derivative contracts (“over-collateralization”), the current replacement cost is zero and the multiplier is less than one (i.e. the PFE component is less than the full value of the aggregate add-on).
6.25. This multiplier will also be activated when the current value of the derivative transactions is negative. This is because out-of-the-money transactions do not currently represent an exposure and have less chance to go in-the-money. The formula for the multiplier is as follows, where:
(1) exp(…) is the exponential function
(2) Floor is 5%
(3) V is the value of the derivative transactions in the netting set
(4) C is the haircut value of net collateral held
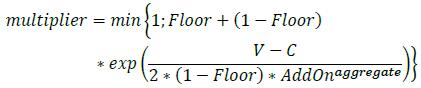
Aggregate add-on and asset classes
6.26. To calculate the aggregate add-on, banks must calculate add-ons for each asset class within the netting set. The SA-CCR uses the following five asset classes:
(1) Interest rate derivatives
(2) Foreign exchange derivatives
(3) Credit derivatives
(4) Equity derivatives.
(5) Commodity derivatives
6.27. Diversification benefits across asset classes are not recognized. Instead, the respective add-ons for each asset class are simply aggregated using the following formula (where the sum is across the asset classes):
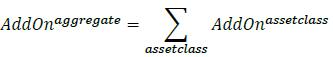
Allocation of derivative transactions to one or more asset classes
6.28. The designation of a derivative transaction to an asset class is to be made on the basis of its primary risk driver. Most derivative transactions have one primary risk driver, defined by its reference underlying instrument (e.g. an interest rate curve for an interest rate swap, a reference entity for a credit default swap, a foreign exchange rate for a foreign exchange (FX) call option, etc.). When this primary risk driver is clearly identifiable, the transaction will fall into one of the asset classes described above.
6.29. For more complex trades that may have more than one risk driver (e.g. multi-asset or hybrid derivatives), banks must take sensitivities and volatility of the underlying into account for determining the primary risk driver
6.30. SAMA may also require more complex trades to be allocated to more than one asset class, resulting in the same position being included in multiple classes. In this case, for each asset class to which the position is allocated, banks must determine appropriately the sign and delta adjustment of the relevant risk driver (the role of delta adjustments in SA-CCR is outlined further in 6.32 below).
General steps for calculating the PFE add-on for each asset class
6.31. For each transaction, the primary risk factor or factors need to be determined and attributed to one or more of the five asset classes: interest rate, foreign exchange, credit, equity or commodity. The add-on for each asset class is calculated using asset-class-specific formulas.13
6.32. Although the formulas for the asset class add-ons vary between asset classes, they all use the following general steps:
(6) The effective notional (D) must be calculated for each derivative (i.e. each individual trade) in the netting set. The effective notional is a measure of the sensitivity of the trade to movements in underlying risk factors (i.e. interest rates, exchange rates, credit spreads, equity prices and commodity prices). The effective notional is calculated as the product of the following parameters (i.e. D = d * MF * δ):
(a) The adjusted notional (d). The adjusted notional is a measure of the size of the trade. For derivatives in the foreign exchange asset class this is simply the notional value of the foreign currency leg of the derivative contract, converted to the Saudi Riyal (SAR). For derivatives in the equity and commodity asset classes, it is simply the current price of the relevant share or unit of commodity multiplied by the number of shares /units that the derivative references. For derivatives in the interest rate and credit asset classes, the notional amount is adjusted by a measure of the duration of the instrument to account for the fact that the value of instruments with longer durations are more sensitive to movements in underlying risk factors (i.e. interest rates and credit spreads).
(b) The maturity factor (MF). The maturity factor is a parameter that takes account of the time period over which the potential future exposure is calculated. The calculation of the maturity factor varies depending on whether the netting set is margined or unmargined.
(c) The supervisory delta (δ). The supervisory delta is used to ensure that the effective notional take into account the direction of the trade, i.e. whether the trade is long or short, by having a positive or negative sign. It is also takes into account whether the trade has a non-linear relationship with the underlying risk factor (which is the case for options and collateralized debt obligation tranches).
(7) A supervisory factor (SF) is identified for each individual trade in the netting set. The supervisory factor is the supervisory specified change in value of the underlying risk factor on which the potential future exposure calculation is based, which has been calibrated to take into account the volatility of underlying risk factors.
(8) The trades within each asset class are separated into supervisory specified hedging sets. The purpose of the hedging sets is to group together trades within the netting set where long and short positions should be permitted to offset each other in the calculation of potential future exposure.
(9) Aggregation formulas are applied to aggregate the effective notionals and supervisory factors across all trades within each hedging set and finally at the asset-class level to give the asset class level add-on. The method of aggregation varies between asset classes and for credit, equity and commodity derivatives it also involves the application of supervisory correlation parameters to capture diversification of trades and basis risk.
Time period parameters: Mi, Ei, Si and Ti
6.33. There are four time period parameters that are used in the SA-CCR (all expressed in years):
(1) For all asset classes, the maturity Mi of a contract is the time period (starting today) until the latest day when the contract may still be active. This time period appears in the maturity factor defined in 6.51 to 6.56 that scales down the adjusted notionals for unmargined trades for all asset classes. If a derivative contract has another derivative contract as its underlying (for example, a swaption) and may be physically exercised into the underlying contract (i.e. a bank would assume a position in the underlying contract in the event of exercise), then maturity of the contract is the time period until the final settlement date of the underlying derivative contract.
(2) For interest rate and credit derivatives, Siis the period of time (starting today) until start of the time period referenced by an interest rate or credit contract. If the derivative references the value of another interest rate or credit instrument (e.g. swaption or bond option), the time period must be determined on the basis of the underlying instrument. Si appears in the definition of supervisory duration defined in 6.36.
(3) For interest rate and credit derivatives, Ei is the period of time (starting today) until the end of the time period referenced by an interest rate or credit contract. If the derivative references the value of another interest rate or credit instrument (e.g. swaption or bond option), the time period must be determined on the basis of the underlying instrument. Ei appears in the definition of supervisory duration defined in 6.36. In addition, Ei is used for allocating derivatives in the interest rate asset class to maturity buckets, which are used in the calculation of the asset class add-on (see 6.60(3)).
(4) For options in all asset classes, Ti is the time period (starting today) until the latest contractual exercise date as referenced by the contract. This period shall be used for the determination of the option’s supervisory delta in 6.40 to 6.43.
6.34. Table 1 includes example transactions and provides each transaction’s related maturity Mi, start date Si and end date Ei. In addition, the option delta in 6.40 to 6.43 depends on the latest contractual exercise date Ti (not separately shown in the table).
Table 1: Example transactions and related (maturity Mi, start date Si and end date Ei) Instrument Mi Si Ei Interest rate or credit default swap maturing in 10 years 10 years 0 10 years 10-year interest rate swap, forward starting in 5 years 15 years 5 years 15 years Forward rate agreement for time period starting in 6 months and ending in 12 months 1 year 0.5 year 1 years Cash-settled European swaption referencing 5-year interest rate swap with exercise date in 6 months 0.5 year 0.5 year 5.5 year Physically-settled European swaption referencing 5-year interest rate swap with exercise date in 6 months 5.5 years 0.5 year 5.5 years 10-year Bermudan swaption with annual exercise dates 10 years 1 year 10 years Interest rate cap or floor specified for semiannual interest rate with maturity 5 years 5 years 0 5 years Option on a bond maturing in 5 years with the latest exercise date in 1 year 1 year 1 year 5 years 3-month Eurodollar futures that matures in 1 year 1 year 1 year 1.25 years Futures on 20-year treasury bond that matures in 2 years 2 years 2 years 22 years 6-month option on 2-year futures on 20-year treasury bond 2 years 2 years 22 years Trade-level adjusted notional (for trade i): di
6.35. The adjusted notionals are defined at the trade level and take into account both the size of a position and its maturity dependency, if any.
6.36. For interest rate and credit derivatives, the trade-level adjusted notional is the product of the trade notional amount, converted to the Saudi Riyal (SAR), and the supervisory duration SD, which is given by the formula below (i.e.di = notional * SDi). The calculated value of SDi is floored at ten business days.14 If the start date has occurred (e.g. an ongoing interest rate swap), Si must be set to zero.
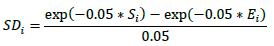
6.37. For foreign exchange derivatives, the adjusted notional is defined as the notional of the foreign currency leg of the contract, converted to the Saudi Riyal (SAR). If both legs of a foreign exchange derivative are denominated in currencies other than the Saudi Riyal (SAR), the notional amount of each leg is converted to the Saudi Riyal (SAR) and the leg with the larger Saudi Riyal (SAR) value is the adjusted notional amount.
6.38. For equity and commodity derivatives, the adjusted notional is defined as the product of the current price of one unit of the stock or commodity (e.g. a share of equity or barrel of oil) and the number of units referenced by the trade.
6.39. In many cases the trade notional amount is stated clearly and fixed until maturity. When this is not the case, banks must use the following rules to determine the trade notional amount.
(1) Where the notional is a formula of market values, the bank must enter the current market values to determine the trade notional amount.
(2) For all interest rate and credit derivatives with variable notional amounts specified in the contract (such as amortizing and accreting swaps), banks must use the average notional over the remaining life of the derivative as the trade notional amount. The average should be calculated as “time weighted”. The averaging described in this paragraph does not cover transactions where the notional varies due to price changes (typically, FX, equity and commodity derivatives).
(3) Leveraged swaps must be converted to the notional of the equivalent unleveraged swap, that is, where all rates in a swap are multiplied by a factor, the stated notional must be multiplied by the factor on the interest rates to determine the trade notional amount.
(4) For a derivative contract with multiple exchanges of principal, the notional is multiplied by the number of exchanges of principal in the derivative contract to determine the trade notional amount.
(5) For a derivative contract that is structured such that on specified dates any outstanding exposure is settled and the terms are reset so that the fair value of the contract is zero, the remaining maturity equals the time until the next reset date.
Supervisory delta adjustment
6.40. The supervisory delta adjustment (δi) parameters are also defined at the trade i level and are applied to the adjusted notional amounts to reflect the direction of the transaction and its non-linearity.15
6.41. The delta adjustments for all instruments that are not options and are not collateralized debt obligation (CDO) tranches are as set out in the table below:16
δi Long in the primary risk factor Short in the primary risk factor Instruments that are not options or CDO tranches +1 -1 6.42. The delta adjustments for options are set out in the table below, where:
(1) The following are parameters that banks must determine appropriately:
(a) Pi: Underlying price (spot, forward, average, etc.)
(b) Ki: Strike price
(c) Ti: Latest contractual exercise date of the option
(2) The supervisory volatility σi an option is specified on the basis of supervisory factor applicable to the trade (see Table 2 in 6.75).
(3) The symbol Φ represents the standard normal cumulative distribution function.
δi Bought Sold Call Option 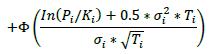
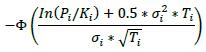
Put Option 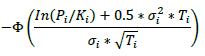
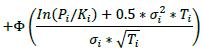
Delta (δ) Bought Sold Call Option 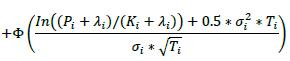
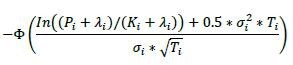
Put Option 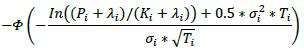
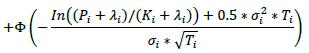
6.43. The delta adjustments for CDO tranches17 are set out in the table below, where the following are parameters that banks must determine appropriately:
(1) Ai: Attachment point of the CDO tranche
(2) Di: Detachment point of the CDO tranche
δi Purchased (long protection) Sold (Short protection) CDO tranche s 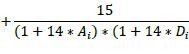
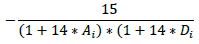
Effective notional for options
6.44. For single-payment options the effective notional (i.e. D = d * MF * δ) is calculated using the following specifications:
(1) For European, Asian, American and Bermudan put and call options, the supervisory delta must be calculated using the simplified Black-Scholes formula referenced in 6.42. In the case of Asian options, the underlying price must be set equal to the current value of the average used in the payoff. In the case of American and Bermudan options, the latest allowed exercise date must be used as the exercise date Ti in the formula.
(2) For Bermudan swaptions, the start date Si must be equal to the earliest allowed exercise date, while the end date Ei must be equal to the end date of the underlying swap.
(3) For digital options, the payoff of each digital option (bought or sold) with strike Ki must be approximated via the “collar” combination of bought and sold European options of the same type (call or put), with the strikes set equal to 0.95.Ki and 1.05.Ki. The size of the position in the collar components must be such that the digital payoff is reproduced exactly outside the region between the two strikes. The effective notional is then computed for the bought and sold European components of the collar separately, using the option formulae for the supervisory delta referenced in 6.42 (the exercise date Tiand the current value of the underlying Pi of the digital option must be used). The absolute value of the digital-option effective notional must be capped by the ratio of the digital payoff to the relevant supervisory factor.
(4) If a trade’s payoff can be represented as a combination of European option payoffs (e.g. collar, butterfly/calendar spread, straddle, strangle), each European option component must be treated as a separate trade.
6.45. For the purposes of effective notional calculations, multiple-payment options may be represented as a combination of single-payment options. In particular, interest rate caps/floors may be represented as the portfolio of individual caplets /floorlets, each of which is a European option on the floating interest rate over a specific coupon period. For each caplet/floorlet, Si and Tiare the time periods starting from the current date to the start of the coupon period, while Ei is the time period starting from the current date to the end of the coupon period.
6.46. In the case of options (e.g. interest rate caps/floors that may be represented as the portfolio of individual caplets/floorlets), banks may decompose those products in a manner consistent with 6.45. Banks may not decompose linear products (e.g. ordinary interest rate swaps).
Supervisory factors: SFi
6.47. Supervisory factors (SFi) are used, together with aggregation formulas, to convert effective notional amounts into the add-on for each hedging set.18 The way in which supervisory factors are used within the aggregation formulas varies between asset classes. The supervisory factors are listed in Table 2 under 6.75.
Hedging sets
6.48. The hedging sets in the different asset classes are defined as follows, except for those described in 6.49 and 6.50:
(1) Interest rate derivatives consist of a separate hedging set for each currency.
(2) FX derivatives consist of a separate hedging set for each currency pair.
(3) Credit derivatives consist of a single hedging set.
(4) Equity derivatives consist of a single hedging set.
(5) Commodity derivatives consist of four hedging sets defined for broad categories of commodity derivatives: energy, metals, agricultural and other commodities.
6.49. Derivatives that reference the basis between two risk factors and are denominated in a single currency19 (basis transactions) must be treated within separate hedging sets within the corresponding asset class. There is a separate hedging set20 for each pair of risk factors (i.e. for each specific basis). Examples of specific bases include three-month Libor versus six-month Libor, three-month Libor versus three-month T-Bill, one-month Libor versus overnight indexed swap rate, Brent Crude oil versus Henry Hub gas. For hedging sets consisting of basis transactions, the supervisory factor applicable to a given asset class must be multiplied by one-half.
6.50. Derivatives that reference the volatility of a risk factor (volatility transactions) must be treated within separate hedging sets within the corresponding asset class. Volatility hedging sets must follow the same hedging set construction outlined in 6.48 (for example, all equity volatility transactions form a single hedging set). Examples of volatility transactions include variance and volatility swaps, options on realized or implied volatility. For hedging sets consisting of volatility transactions, the supervisory factor applicable to a given asset class must be multiplied by a factor of five.21
Maturity factors
6.51. The minimum time risk horizon for an unmargined transaction is the lesser of one year and the remaining maturity of the derivative contract, floored at ten business days.22 Therefore, the calculation of the effective notional for an unmargined transaction includes the following maturity factor, where Mi is the remaining maturity of transaction i, floored at 10 business days:
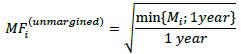
6.52. The maturity parameter (Mi) is expressed in years but is subject to a floor of 10 business days. Banks should use standard market convention to convert business days into years, and vice versa. For example, 250 business days in a year, which results in a floor of 10/250 years for Mi.
6.53. For margined transactions, the maturity factor is calculated using the margin period of risk (MPOR), subject to specified floors. That is, banks must first estimate the margin period of risk (as defined in 4.17) for each of their netting sets. They must then use the higher of their estimated margin period of risk and the relevant floor in the calculation of the maturity factor (6.55). The floors for the margin period of risk are as follows:
(1) Ten business days for non-centrally-cleared transactions subject to daily margin agreements.
(2) The sum of nine business days plus the re-margining period for non-centrally cleared transactions that are not subject daily margin agreements.
(3) The relevant floors for centrally cleared transactions are prescribed in the capital requirements for bank exposures to central counterparties (see in Chapter 8 of this framework).
6.54. The following are exceptions to the floors on the minimum margin period of risk set out in 6.53 above:
(1) For netting sets consisting of more than 5000 transactions that are not with a central counterparty the floor on the margin period of risk is 20 business days.
(2) For netting sets containing one or more trades involving either illiquid collateral, or an OTC derivative that cannot be easily replaced, the floor on the margin period of risk is 20 business days. For these purposes, "Illiquid collateral" and "OTC derivatives that cannot be easily replaced" must be determined in the context of stressed market conditions and will be characterized by the absence of continuously active markets where a counterparty would, within two or fewer days, obtain multiple price quotations that would not move the market or represent a price reflecting a market discount (in the case of collateral) or premium (in the case of an OTC derivative). Examples of situations where trades are deemed illiquid for this purpose include, but are not limited to, trades that are not marked daily and trades that are subject to specific accounting treatment for valuation purposes (e.g. OTC derivatives transactions referencing securities whose fair value is determined by models with inputs that are not observed in the market).
(3) If a bank has experienced more than two margin call disputes on a particular netting set over the previous two quarters that have lasted longer than the applicable margin period of risk (before consideration of this provision), then the bank must reflect this history appropriately by doubling the applicable supervisory floor on the margin period of risk for that netting set for the subsequent two quarters.
(4) In the case of non-centrally cleared derivatives that are subject to the requirements under Margin requirements, 6.55(3) applies only to variation margin call disputes.
6.55. The calculation of the effective notional for a margined transaction includes the following maturity factor, where MPORi is the margin period of risk appropriate for the margin agreement containing the transaction i (subject to the floors set out in 6.53 and 6.54 above).
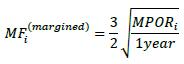
6.56. The margin period of risk (MPORi) is often expressed in days, but the calculation of the maturity factor for margined netting sets references 1 year in the denominator. Banks should use standard market convention to convert business days into years, and vice versa. For example, 1 year can be converted into 250 business days in the denominator of the MF formula if MPOR is expressed in business days. Alternatively, the MPOR expressed in business days can be converted into years by dividing it by 250.
Supervisory correlation parameters
6.57. The supervisory correlation parameters (ρi) only apply to the PFE add-on calculation for equity, credit and commodity derivatives, and are set out in Table 2 under 6.75. For these asset classes, the supervisory correlation parameters are derived from a single-factor model and specify the weight between systematic and idiosyncratic components. This weight determines the degree of offset between individual trades, recognizing that imperfect hedges provide some, but not perfect, offset. Supervisory correlation parameters do not apply to interest rate and foreign exchange derivatives.
Asset class level add-ons
6.58. As set out in 6.27, the aggregate add-on for a netting set (AddOnaggregate) is calculated as the sum of the add-ons calculated for each asset class within the netting set. The sections that follow set out the calculation of the add-on for each asset class.
Add-on for interest rate derivatives
6.59. The calculation of the add-on for the interest rate derivative asset class captures the risk of interest rate derivatives of different maturities being imperfectly correlated. It does this by allocating trades to maturity buckets, in which full offsetting of long and short positions is permitted, and by using an aggregation formula that only permits limited offsetting between maturity buckets. This allocation of derivatives to maturity buckets and the process of aggregation (steps 3 to 5 below) are only used in the interest rate derivative asset class.
6.60. The add-on for the interest rate derivative asset class (AddOnIR) within a netting set is calculated using the following steps:
(1) Step 1: Calculate the effective notional for each trade in the netting set that is in the interest rate derivative asset class. This is calculated as the product of the following three terms:
(i) the adjusted notional of the trade (d);
(ii) the supervisory delta adjustment of the trade (S); and
(iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di= di* MFi* δi, where each term is as defined in 6.35 to 6.56.
(2) Step 2: Allocate the trades in the interest rate derivative [including inflation derivatives] asset class to hedging sets. In the interest rate derivative asset class the hedging sets consist of all the derivatives that reference the same currency.
(3) Step 3: Within each hedging set allocate each of the trades to the following three maturity buckets: less than one year (bucket 1), between one and five years (bucket 2) and more than five years (bucket 3).
(4) Step 4: Calculate the effective notional of each maturity bucket by adding together all the trade level effective notionals calculated in step 1 of the trades within the maturity bucket. Let DB1, DB1 and DB1 be the effective notionals of buckets 1, 2 and 3 respectively.
(5) Step 5: Calculate the effective notional of the hedging set (ENHS ) by using either of the two following aggregation formulas (the latter is to be used if the bank chooses not to recognize offsets between long and short positions across maturity buckets):
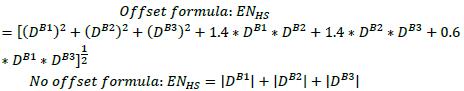
(6) Step 6: Calculate the hedging set level add-on (AddOnHS) by multiplying the effective notional of the hedging set (ENHS) by the prescribed supervisory factor (SFHS). The prescribed supervisory factor in the interest rate asset class is set at 0.5%, which means that AddOnHS= ENHS * 0.005.
(7) Step 7: Calculate the asset class level add-on (AddOnIR) by adding together all of the hedging set level add-ons calculated in step 6:
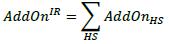
Add-on for foreign exchange derivatives
6.61. The steps to calculate the add-on for the foreign exchange derivative asset class are similar to the steps for the interest rate derivative asset class, except that there is no allocation of trades to maturity buckets (which means that there is full offsetting of long and short positions within the hedging sets of the foreign exchange derivative asset class).
6.62. The add-on for the foreign exchange derivative asset class (AddOnFX) within a netting set is calculated using the following steps:
(1) Step 1: Calculate the effective notional for each trade in the netting set that is in the foreign exchange derivative asset class. This is calculated as the product of the following three terms: (i) the adjusted notional of the trade (d); (ii) the supervisory delta adjustment of the trade (δ); and (iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di = di* MFi * δi, where each term is as defined in 6.35 to 6.56.
(2) Step 2: Allocate the trades in the foreign exchange derivative asset class to hedging sets. In the foreign exchange derivative asset class the hedging sets consist of all the derivatives that reference the same currency pair.
(3) Step 3: Calculate the effective notional of each hedging set (ENHS) by adding together the trade level effective notionals calculated in step 1.
(4) Step 4: Calculate the hedging set level add-on (AddOnHS) by multiplying the HS absolute value of the effective notional of the hedging set (ENHS) by the HS prescribed supervisory factor (SFHS). The prescribed supervisory factor in the HS foreign exchange derivative asset class is set at 4%, which means that AddOnHS= |ENHS| * 0.04.
(5) Step 5: Calculate the asset class level add-on (AddOnFX) by adding together all of the hedging set level add-ons calculated in step 5:
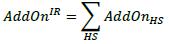
Add-on for credit derivatives
6.63. The calculation of the add-on for the credit derivative asset class only gives full recognition of the offsetting of long and short positions for derivatives that reference the same entity (e.g. the same corporate issuer of bonds). Partial offsetting is recognized between derivatives that reference different entities in step 4 below. The formula used in step 4 is explained further in 6.65 to 6.67.
6.64. The add-on for the credit derivative asset class (AddOnCredlt ) within a netting set is calculated using the following steps:
(1) Step 1: Calculate the effective notional for each trade in the netting set that is in the credit derivative asset class. This is calculated as the product of the following three terms:
(i) the adjusted notional of the trade (d);
(ii) the supervisory delta adjustment of the trade (δ); and
(iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di= di* MFi * δi, where each term is as defined in 6.35 to 6.56.
(2) Step 2: Calculate the combined effective notional for all derivatives that reference the same entity. Each separate credit index that is referenced by derivatives in the credit derivative asset class should be treated as a separate entity. The combined effective notional of the entity (ENentity) is calculated by adding together the trade level effective notionals calculated in step 1 that reference that entity.
(3) Step 3: Calculate the add-on for each entity (AddOnentity) by multiplying the entity combined effective notional for that entity calculated in step 2 by the supervisory factor that is specified for that entity (SFentity). The supervisory entity factors vary according to the credit rating of the entity in the case of single name derivatives, and whether the index is considered investment grade or non-investment grade in the case of derivatives that reference an index. The supervisory factors are set out in Table 2 in 6.75.
(4) Step 4: Calculate the asset class level add-on (AddOnCredlt) by using the formula that follows. In the formula the summations are across all entities referenced by the derivatives, AddOnentity is the add-on amount calculated entity in step 3 for each entity referenced by the derivatives and ρ is the entity supervisory prescribed correlation factor corresponding to the entity. As set out in Table 2 in 6.75, the correlation factor is 50% for single entities and 80% for indices.
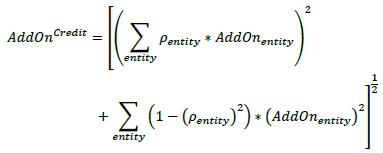
6.65. The formula to recognize partial offsetting in 6.64(4) above, is a single-factor model, which divides the risk of the credit derivative asset class into a systematic component and an idiosyncratic component. The entity-level add-ons are allowed to offset each other fully in the systematic component; whereas, there is no offsetting benefit in the idiosyncratic component. These two components are weighted by a correlation factor which determines the degree of offsetting / hedging benefit within the credit derivatives asset class. The higher the correlation factor, the higher the importance of the systematic component, hence the higher the degree of offsetting benefits.
6.66. It should be noted that a higher or lower correlation does not necessarily mean a higher or lower capital requirement. For portfolios consisting of long and short credit positions, a high correlation factor would reduce the charge. For portfolios consisting exclusively of long positions (or short positions), a higher correlation factor would increase the charge. If most of the risk consists of systematic risk, then individual reference entities would be highly correlated and long and short positions should offset each other. If, however, most of the risk is idiosyncratic to a reference entity, then individual long and short positions would not be effective hedges for each other.
6.67. The use of a single hedging set for credit derivatives implies that credit derivatives from different industries and regions are equally able to offset the systematic component of an exposure, although they would not be able to offset the idiosyncratic portion. This approach recognizes that meaningful distinctions between industries and/or regions are complex and difficult to analyze for global conglomerates.
Add-on for equity derivatives
6.68. The calculation of the add-on for the equity derivative asset class is very similar to the calculation of the add-on for the credit derivative asset class. It only gives full recognition of the offsetting of long and short positions for derivatives that reference the same entity (e.g. the same corporate issuer of shares). Partial offsetting is recognized between derivatives that reference different entities in step 4 below.
6.69. The add-on for the equity derivative asset class (AddOnEquity) within a netting set is calculated using the following steps:
(1) Step 1: Calculate the effective notional for each trade in the netting set that is in the equity derivative asset class. This is calculated as the product of the following three terms:
(i) the adjusted notional of the trade (d);
(ii) the supervisory delta adjustment of the trade (δ); and
(iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di= di* MFi* δi, where each term is as defined in 6.35 to 6.56.
(2) Step 2: Calculate the combined effective notional for all derivatives that reference the same entity. Each separate equity index that is referenced by derivatives in the equity derivative asset class should be treated as a separate entity. The combined effective notional of the entity (ENentity) is calculated entity by adding together the trade level effective notionals calculated in step 1 that reference that entity.
(3) Step 3: Calculate the add-on for each entity (AddOnentity) by multiplying the entity combined effective notional for that entity calculated in step 2 by the supervisory factor that is specified for that entity (SFentity). The supervisory entity factors are set out in Table 2 in 6.75 and vary according to whether the entity is a single name (SFentity = 32%) or an index (SFentity = 20%).
(4) Step 4: Calculate the asset class level add-on (AddOnEquity) by using the formula that follows. In the formula the summations are across all entities referenced by the derivatives, AddOnentity is the add-on amount calculated entity in step 3 for each entity referenced by the derivatives and ρentity is the entity supervisory prescribed correlation factor corresponding to the entity. As set out in Table 2 in 6.75, the correlation factor is 50% for single entities and 80% for indices.
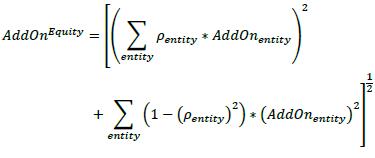
6.70. The supervisory factors for equity derivatives were calibrated based on estimates of the market volatility of equity indices, with the application of a conservative beta factor23 to translate this estimate into an estimate of individual volatilities.
6.71. Banks are not permitted to make any modelling assumptions in the calculation of the PFE add-ons, including estimating individual volatilities or taking publicly available estimates of beta. This is a pragmatic approach to ensure a consistent implementation across jurisdictions but also to keep the add-on calculation relatively simple and prudent. Therefore, bank must only use the two values of supervisory factors that are defined for equity derivatives, one for single entities and one for indices.
Add-on for commodity derivatives
6.72. The calculation of the add-on for the commodity derivative asset class is similar to the calculation of the add-on for the credit and equity derivative asset classes. It recognizes the full offsetting of long and short positions for derivatives that reference the same type of underlying commodity. It also allows partial offsetting between derivatives that reference different types of commodity, however, this partial offsetting is only permitted within each of the four hedging sets of the commodity derivative asset class, where the different commodity types are more likely to demonstrate some stable, meaningful joint dynamics. Offsetting between hedging sets is not recognized (e.g., a forward contract on crude oil cannot hedge a forward contract on corn).
6.73. The add-on for the commodity derivative asset class (AddOnCommodlty) within a netting set is calculated using the following steps:
(1) Step 1: Calculate the effective notional for each trade in the netting set that is in the commodity derivative asset class. This is calculated as the product of the following three terms:
(i) the adjusted notional of the trade (d);
(ii) the supervisory delta adjustment of the trade (δ); and
(iii) the maturity factor (MF). That is, for each trade i, the effective notional Di is calculated as Di— di * MFi * δi, where each term is as defined in 6.35 to 6.56.
(2) Step 2: Allocate the trades in commodity derivative asset class to hedging sets. In the commodity derivative asset class there are four hedging sets consisting of derivatives that reference: energy, metals, agriculture and other commodities.
(3) Step 3: Calculate the combined effective notional for all derivatives with each hedging set that reference the same commodity type (e.g. all derivative that reference copper within the metals hedging set). The combined effective notional of the commodity type (ENComTyoe) is calculated by adding ComType together the trade level effective notionals calculated in step 1 that reference that commodity type.
(4) Step 4: Calculate the add-on for each commodity type (AddOnComType) within each hedging set by multiplying the combined effective notional for that commodity calculated in step 3 by the supervisory factor that is specified for that commodity type (SFComType). The supervisory factors are ComType set out in Table 2 in 6.75 and are set at 40% for electricity derivatives and 18% for derivatives that reference all other types of commodities.
(5) Step 5: Calculate the add-on for each of the four commodity hedging sets (AddOnHS) by using the formula that follows. In the formula the summations are across all commodity types within the hedging set, AddOnComType is the add-on amount ComType calculated in step 4 for each commodity type and ρComTyoe is the supervisory ComType prescribed correlation factor corresponding to the commodity type. As set out in Table 2 in 6.75, the correlation factor is set at 40% for all commodity types.
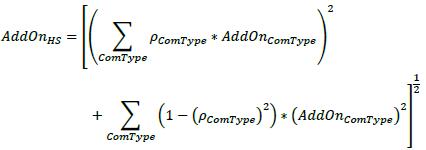
(6) Step 6: Calculate the asset class level add-on (AddOnCommodlty) by adding together all of the hedging set level add-ons calculated in step 5:
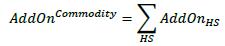
6.74. Regarding the calculation steps above, defining individual commodity types is operationally difficult. In fact, it is impossible to fully specify all relevant distinctions between commodity types so that all basis risk is captured. For example crude oil could be a commodity type within the energy hedging set, but in certain cases this definition could omit a substantial basis risk between different types of crude oil (West Texas Intermediate, Brent, Saudi Light, etc.) Also, the four commodity type hedging sets have been defined without regard to characteristics such as location and quality. For example, the energy hedging set contains commodity types such as crude oil, electricity, natural gas and coal. SAMA may require banks to use more refined definitions of commodities when they are significantly exposed to the basis risk of different products within those commodity types.
Supervisory specified parameters
6.75. Table 2 includes the supervisory factors, correlations and supervisory option volatility add-ons for each asset class and subclass.
Table 2: Summary table of supervisory parameters Asset Class Subclass Supervisory factor Correlation Supervisory option volatility Interest rate 0.50% N/A 50% Foreign exchange 4.0% N/A 15% Credit, Single Name AAA 0.38% 50% 100% AA 0.38% 50% 100% A 0.42% 50% 100% BBB 0.54% 50% 100% BB 1.06% 50% 100% B 1,6% 50% 100% CCC 6.0% 50% 100% Credit, Index IG 0.38% 80% 80% SG 1.06% 80% 80% Equity, Single Name 32% 50% 120% Equity, Index 20% 80% 75% Commodity Electricity 40% 40% 150% Oil/Gas 18% 40% 70% Metals 18% 40% 70% Agricultural 18% 40% 70% Other 18% 40% 70% 6.76. For a hedging set consisting of basis transactions, the supervisory factor applicable to its relevant asset class must be multiplied by one-half. For a hedging set consisting of volatility transactions, the supervisory factor applicable to its relevant asset class must be multiplied by a factor of five.
Treatment of multiple margin agreements and multiple netting sets
6.77. If multiple margin agreements apply to a single netting set, the netting set must be divided into sub-netting sets that align with their respective margin agreement. This treatment applies to both RC and PFE components.
6.78. If a single margin agreement applies to several netting sets, special treatment is necessary because it is problematic to allocate the common collateral to individual netting sets. The replacement cost at any given time is determined by the sum of two terms. The first term is equal to the unmargined current exposure of the bank to the counterparty aggregated across all netting sets within the margin agreement reduced by the positive current net collateral (i.e. collateral is subtracted only when the bank is a net holder of collateral). The second term is non-zero only when the bank is a net poster of collateral: it is equal to the current net posted collateral (if there is any) reduced by the unmargined current exposure of the counterparty to the bank aggregated across all netting sets within the margin agreement. Net collateral available to the bank should include both VM and NICA. Mathematically, RC for the entire margin agreement is calculated as follows, where:
(1) where the summation NS ϵ MA is across the netting sets covered by the margin agreement (hence the notation)
(2) V is the current mark-to-market value of the netting set NS and CMA is the cash equivalent value of all currently available collateral under the margin agreement
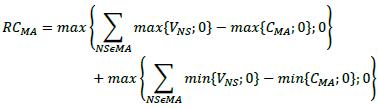
6.79. Where a single margin agreement applies to several netting sets as described in 6.78 above, collateral will be exchanged based on mark-to-market values that are netted across all transactions covered under the margin agreement, irrespective of netting sets. That is, collateral exchanged on a net basis may not be sufficient to cover PFE. In this situation, therefore, the PFE add-on must be calculated according to the unmargined methodology. Netting set-level PFEs are then aggregated using the following formula, where is the 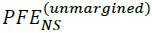 addon for the netting set NS calculated according to the unmargined requirements:
addon for the netting set NS calculated according to the unmargined requirements:
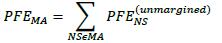
Treatment of collateral taken outside of netting sets
6.80. Eligible collateral which is taken outside a netting set, but is available to a bank to offset losses due to counterparty default on one netting set only, should be treated as an independent collateral amount associated with the netting set and used within the calculation of replacement cost under 6.12 when the netting set is unmargined and under 6.20 when the netting set is margined. Eligible collateral which is taken outside a netting set, and is available to a bank to offset losses due to counterparty default on more than one netting set, should be treated as collateral taken under a margin agreement applicable to multiple netting sets, in which case the treatment under 6.78 and 6.79 applies. If eligible collateral is available to offset losses on non-derivatives exposures as well as exposures determined using the SA-CCR, only that portion of the collateral assigned to the derivatives may be used to reduce the derivatives exposure.
13 The formulas for calculating the asset class add-ons represent stylized Effective EPE calculations under the assumption that all trades in the asset class have zero current mark-to-market value (i.e. they are at-the-money).
14 Note there is a distinction between the time period of the underlying transaction and the remaining maturity of the derivative contract. For example, a European interest rate swaption with expiry of 1 year and the term of the underlying swap of 5 years has S = 1 year and E = 6 i years.
15 Whenever appropriate, the forward (rather than spot) value of the underlying in the supervisory delta adjustments formula should be used in order to account for the risk-free rate as well as for possible cash flows prior to the option expiry (such as dividends).
16 “Long in the primary risk factor” means that the market value of the instrument increases when the value of the primary risk factor increases. “Short in the primary risk factor” means that the market value of the instrument decreases when the value of the primary risk factor increases.
17 First-to-default, second-to-default and subsequent-to-default credit derivative transactions should be treated as CDO tranches under SACCR. For an nth-to-default transaction on a pool of m reference names, banks must use an attachment point of A=(n–1)/m and a detachment point of D=n/m in order to calculate the supervisory delta formula set out 6.43.
18 Each factor has been calibrated to result in an add-on that reflects the Effective EPE of a single at- the-money linear trade of unit notional and one-year maturity. This includes the estimate of realized volatilities assumed by supervisors for each underlying asset class.
19 Derivatives with two floating legs that are denominated in different currencies (such as cross-currency swaps) are not subject to this treatment; rather, they should be treated as non-basis foreign exchange contracts.
20 Within this hedging set, long and short positions are determined with respect to the basis.
21 For equity and commodity volatility transactions, the underlying volatility or variance referenced by the transaction should replace the unit price and contractual notional should replace the number of units.
22 For example, remaining maturity for a one-month option on a 10-year Treasury bond is the one-month to expiration date of the derivative contract. However, the end date of the transaction is the 10- year remaining maturity on the Treasury bond.
23 The beta of an individual equity measures the volatility of the stock relative to a broad market index. A value of beta greater than one means the individual equity is more volatile than the index. The greater the beta is, the more volatile the stock. The beta is calculated by running a linear regression of the stock on the broad index.

