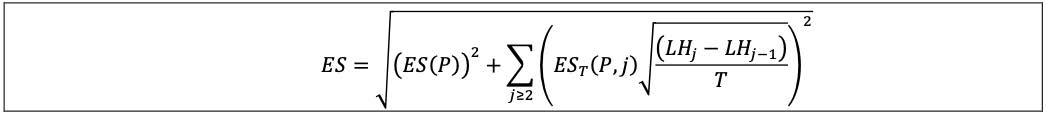| 13.1 | Banks will have flexibility in devising the precise nature of their expected shortfall (ES) models, but the following minimum standards will apply for the purpose of calculating market risk capital requirements. Banks subject to SAMA approval can apply stricter standards.
| |
The IMA does not require all products to be simulated on full revaluation. Simplifications (eg sensitivities-based valuation) may be used provided SAMA agrees that the method used is adequate for the instruments covered.
| |
| 13.2 | ES must be computed on a daily basis for the bank-wide internal models to determine market risk capital requirements. ES must also be computed on a daily basis for each trading desk that uses the internal models approach (IMA).
| |
| 13.3 | In calculating ES, a bank must use a 97.5th percentile, one-tailed confidence level.
| |
| 13.4 | In calculating ES, the liquidity horizons described in [13.12] must be reflected by scaling an ES calculated on a base horizon. The ES for a liquidity horizon must be calculated from an ES at a base liquidity horizon of 10 days with scaling applied to this base horizon result as expressed below, where:
| |
| | (1) | ES is the regulatory liquidity-adjusted ES;
|
| | (2) | T is the length of the base horizon, ie 10 days;
|
| | (3) | EST(P) is the ES at horizon T of a portfolio with positions P = (pi) with respect to shocks to all risk factors that the positions P are exposed to;
|
| | (4) | EST(P, j) is the ES at horizon T of a portfolio with positions P = (pi) with respect to shocks for each position pi in the subset of risk factors Q(pi, j), with all other risk factors held constant;
|
| | (5) | the ES at horizon T, EST(P) must be calculated for changes in the risk factors, and EST(P, j) must be calculated for changes in the relevant subset Q(pi, j) of risk factors, over the time interval T without scaling from a shorter horizon;
|
| | (6) | Q(pi, j)j is the subset of risk factors for which liquidity horizons, as specified in [13.12], for the desk where pi is booked are at least as long as LHj according to the table below. For example, Q(pi,4) is the set of risk factors with a 60-day horizon and a 120-day liquidity horizon. Note that Q(pi, j) is a subset of Q(pi, j–1);
|
| | (7) | the time series of changes in risk factors over the base time interval T may be determined by overlapping observations; and
|
| | (8) | LHj is the liquidity horizon j, with lengths in the following table:
|
| Liquidity horizons, j | Table 1 | | j | LHj | | 1 | 10 | | 2 | 20 | | 3 | 40 | | 4 | 60 | | 5 | 120 |
|
|
| 13.5 | The ES measure must be calibrated to a period of stress.
| |
| | (1) | Specifically, the ES measure must replicate an ES outcome that would be generated on the bank’s current portfolio if the relevant risk factors were experiencing a period of stress. This is a joint assessment across all relevant risk factors, which will capture stressed correlation measures.
|
| | (2) | This calibration is to be based on an indirect approach using a reduced set of risk factors. Banks must specify a reduced set of risk factors that are relevant for their portfolio and for which there is a sufficiently long history of observations.
|
| | | (a) | This reduced set of risk factors is subject to SAMA approval and must meet the data quality requirements for a modellable risk factor as outlined in [11.12] to [11.24].
| |
| | | (b) | The identified reduced set of risk factors must be able to explain a minimum of 75% of the variation of the full ES model (ie the ES of the reduced set of risk factors should be at least equal to 75% of the fully specified ES model on average measured over the preceding 12- week period).
| |
The indicator that must be maximised for the identification of the stressed period is the aggregate capital requirement for modellable risk factors (IMCC) as per [13.15], it has to be maximised for the modellable risk factors, which implies that ESr,s is maximised, as noted in [13.7].
| |
The reduced set of risk factors must be able to explain a minimum of 75% of the variation of the full ES model at the group level for the aggregate of all desks with IMA model approval.
| |
| 13.6 | The ES for market risk capital purposes is therefore expressed as follows, where:
| |
| | (1) | The ES for the portfolio using the above reduced set of risk factors (ESR,S), is calculated based on the most severe 12-month period of stress available over the observation horizon.
|
| | (2) | ESR,S is then scaled up by the ratio of (i) the current ES using the full set of risk factors to (ii) the current ES measure using the reduced set of factors. For the purpose of this calculation, this ratio is floored at 1.
|
| | | (a) | ESF,C is the ES measure based on the current (most recent) 12-month observation period with the full set of risk factors; and
| |
| | | (b) | ESR,C is the ES measure based on the current period with a reduced set of risk factors.
| |
|
| 13.7 | For measures based on stressed observations (ESR,S), banks must identify the 12-month period of stress over the observation horizon in which the portfolio experiences the largest loss. The observation horizon for determining the most stressful 12 months must, at a minimum, span back to and include 2007. Observations within this period must be equally weighted. Banks must update their 12- month stressed periods at least quarterly, or whenever there are material changes in the risk factors in the portfolio. Whenever a bank updates its 12-month stressed periods it must also update the reduced set of risk factors (as the basis for the calculations of ER,C and ER,S) accordingly.
| |
| 13.8 | For measures based on current observations (ESF,C), banks must update their data sets no less frequently than once every three months and must also reassess data sets whenever market prices are subject to material changes.
| |
| | (1) | This updating process must be flexible enough to allow for more frequent updates.
|
| | (2) | SAMA may also require a bank to calculate its ES using a shorter observation period if, in SAMA’s judgement; this is justified by a significant upsurge in price volatility. In this case, however, the period should be no shorter than six months.
|
| 13.9 | No particular type of ES model is prescribed. Provided that each model used captures all the material risks run by the bank, as confirmed through profit and loss (P&L) attribution (PLA) tests and backtesting, and conforms to each of the requirements set out above and below, SAMA may permit banks to use models based on either historical simulation, Monte Carlo simulation, or other appropriate analytical methods.
| |
| 13.10 | Banks will have discretion to recognise empirical correlations within broad regulatory risk factor classes (interest rate risk, equity risk, foreign exchange risk, commodity risk and credit risk, including related options volatilities in each risk factor category). Empirical correlations across broad risk factor categories will be constrained by SAMA aggregation requirements, as described in [13.14] to [13.15], and must be calculated and used in a manner consistent with the applicable liquidity horizons, clearly documented and able to be explained to SAMA on request.
| |
| 13.11 | Banks’ models must accurately capture the risks associated with options within each of the broad risk categories. The following criteria apply to the measurement of options risk:
| |
| | (1) | Banks’ models must capture the non-linear price characteristics of options positions.
|
| | (2) | Banks’ risk measurement systems must have a set of risk factors that captures the volatilities of the rates and prices underlying option positions, ie vega risk. Banks with relatively large and/or complex options portfolios must have detailed specifications of the relevant volatilities. Banks must model the volatility surface across both strike price and vertex (ie tenor).
|
| 13.12 | As set out in [13.4], a scaled ES must be calculated based on the liquidity horizon n defined below. n is calculated per the following conditions:
| |
| | (1) | Banks must map each risk factor on to one of the risk factor categories shown below using consistent and clearly documented procedures.
|
| | (2) | The mapping of risk factors must be:
|
| | | (a) | set out in writing;
| |
| | | (b) | validated by the bank’s risk management;
| |
| | | (c) | made available to SAMA; and
| |
| | | (d) | subject to internal audit.
| |
| | (3) | n is determined for each broad category of risk factor as set out in Table 2. However, on a desk-by-desk basis, n can be increased relative to the values in the table below (ie the liquidity horizon specified below can be treated as a floor). Where n is increased, the increased horizon must be 20, 40, 60 or 120 days and the rationale must be documented and be subject to SAMA approval. Furthermore, liquidity horizons should be capped at the maturity of the related instrument.
|
| Liquidity horizon n by risk factor | Table 2 | | Risk factor category | n | Risk factor category | n | | Interest rate: specified currencies - EUR, USD, GBP, AUD, JPY, SEK, CAD and domestic currency of a bank | 10 | Equity price (small cap): volatility | 60 | | Interest rate: unspecified currencies | 20 | Equity: other types | 60 | | Interest rate: volatility | 60 | Foreign exchange (FX) rate: specified currency pairs49 | 10 | | Interest rate: other types | 60 | FX rate: currency pairs | 20 | | Credit spread: sovereign (investment grade, or IG) | 20 | FX: volatility | 40 | | Credit spread: sovereign (high yield, or HY) | 40 | FX: other types | 40 | | Credit spread: corporate (IG) | 40 | Energy and carbon emissions trading price | 20 | | Credit spread: corporate (HY) | 60 | Precious metals and non-ferrous metals price | 20 | | Credit spread: volatility | 120 | Other commodities price | 60 | | Credit spread: other types | 120 | Energy and carbon emissions trading price: volatility | 60 | | | Precious metals and non-ferrous metals price: volatility | 60 | | Equity price (large cap) | 10 | Other commodities price: volatility | 120 | | Equity price (small cap) | 20 | Commodity: other types | 120 | | Equity price (large cap): volatility | 20 | |
|
The liquidity horizon for equity large cap repo and dividend risk factors is 20 days. All other equity repo and dividend risk factors are subject to a liquidity horizon of 60 days.
| |
For mono-currency and cross-currency basis risk, the liquidity horizons of 10 days and 20 days for interest rate-specified currencies and unspecified currencies, respectively, applied
| |
The liquidity horizon for inflation risk factors should be consistent with the liquidity horizons for interest rate risk factors for a given currency.
| |
If the maturity of the instrument is shorter than the respective liquidity horizon of the risk factor as prescribed in [13.12], the next longer liquidity horizon length (out of the lengths of 10, 20, 40, 60 or 120 days as set out in the paragraph) compared with the maturity of the instrument itself must be used. For example, although the liquidity horizon for interest rate volatility is prescribed as 60 days, if an instrument matures in 30 days, a 40-day liquidity horizon would apply for the instrument’s interest rate volatility.
| |
To determine the liquidity horizon of multi-sector credit and equity indices, the respective liquidity horizons of the underlying instruments must be used. A weighted average of liquidity horizons of the instruments contained in the index must be determined by multiplying the liquidity horizon of each individual instrument by its weight in the index (ie the weight used to construct the index) and summing across all instruments. The liquidity horizon of the index is the shortest liquidity horizon (out of 10, 20, 40, 60 and 120 days) that is equal to or longer than the weighted average liquidity horizon. For example, if the weighted average liquidity horizon is 12 days, the liquidity horizon of the index would be 20 days.
| |