14- Simplified Standardised Approach
Risk-Weighted Assets and Capital Requirements
14.1 The risk-weighted assets for market risk under the simplified standardized approach are determined by multiplying the capital requirements calculated as set out in this chapter by 12.5.
(1) [14.3] to [14.73] deal with interest rate, equity, foreign exchange (FX) and commodities risk.
(2) [14.74] to [14.86] set out a number of possible methods for measuring the price risk in options of all kinds.
(3) The capital requirement under the simplified standardised approach will be the measures of risk obtained from [14.2] to [14.86], summed arithmetically.
14.2 The capital requirement arising from the simplified standardised approach is the simple sum of the recalibrated capital requirements arising from each of the four risk classes – namely interest rate risk, equity risk, FX risk and commodity risk as detailed in the formula below, where:
(1) CRIRR = capital requirement under [14.3] to [14.40] (interest rate risk), plus additional requirements for option risks from debt instruments (non-delta risks) under [14.74] to [14.86] (treatment of options);
(2) CREQ = capital requirement under [14.41] to [14.52] (equity risk), plus additional requirements for option risks from equity instruments (non-delta risks) under [14.74] to [14.86] (treatment of options);
(3) CRFX = capital requirement under [14.53] to [14.62] (FX risk), plus additional requirements for option risks from foreign exchange instruments (non-delta risks) under [14.74] to [14.86] (treatment of options);
(4) CRCOMM = capital requirement under [14.63] to [14.73] (commodities risk), plus additional requirements for option risks from commodities instruments (non-delta risks) under [14.74] to [14.86] (treatment of options);
(5) CFIRR = Scaling factor of 1.30;
(6) CFEQ = Scaling factor of 3.50;
(7) CFCOMM = Scaling factor of 1.90; and
(8) CFFX = Scaling factor of 1.20.
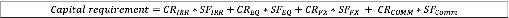
Interest Rate Risk
14.3 This section sets out the simplified standard approach for measuring the risk of holding or taking positions in debt securities and other interest rate related instruments in the trading book. The instruments covered include all fixed-rate and floating-rate debt securities and instruments that behave like them, including non-convertible preference shares.53 Convertible bonds, ie debt issues or preference shares that are convertible, at a stated price, into common shares of the issuer, will be treated as debt securities if they trade like debt securities and as equities if they trade like equities. The basis for dealing with derivative products is considered in [14.31] to [14.40].
14.4 The minimum capital requirement is expressed in terms of two separately calculated amounts, one applying to the “specific risk” of each security, whether it is a short or a long position, and the other to the interest rate risk in the portfolio (termed “general market risk”) where long and short positions in different securities or instruments can be offset.
Specific risk
14.5 The capital requirement for specific risk is designed to protect against an adverse movement in the price of an individual security owing to factors related to the individual issuer. In measuring the risk, offsetting will be restricted to matched positions in the identical issue (including positions in derivatives). Even if the issuer is the same, no offsetting will be permitted between different issues since differences in coupon rates, liquidity, call features, etc mean that prices may diverge in the short run.
Netting is only allowed under limited circumstances for interest rate specific risk as explained in [14.5]: “offsetting will be restricted to matched positions in the identical issue (including positions in derivatives). Even if the issuer is the same, no offsetting will be permitted between different issues since differences in coupon rates, liquidity, call features, etc means that prices may diverge in the short run.” In addition, partial offsetting is allowed in two other sets of circumstances. One set of circumstances is described in [14.21] and concerns nth-to-default basked products. The other set of circumstances described in [14.16] to [14.18] pertains to offsetting between a credit derivative (whether total return swap or credit default swap) and the underlying exposure (ie cash position). Although this treatment applies generally in a one-for-one fashion, it is possible that multiple instruments could combine to create a hedge that would be eligible for consideration for partial offsetting. SAMA recognise that, in the case of multiple instruments comprising one side of the position, necessary conditions (ie the value of two legs moving in opposite directions, key contractual features of the credit derivative, identical reference obligations and currency/maturity mismatches) will be extremely difficult to meet, in practice.
14.6 The Specific risk capital requirements for “government” and “other” categories will be as follows:
Specific risk capital requirements for issuer risk Government and "other" categories Table 1 Categories External credit assessment Specific risk capital requirement Government AAA to AA- 0% A+ to BBB- 0.25% (residual term to final maturity 6 months or less)
1.00% (residual term to final maturity greater than 6 and up to and including 24 months)
1.60% (residual term to final maturity exceeding 24 months)BB+ to B- 8.00% Below B- 12.00% Unrated 8.00% Qualifying 0.25% (residual term to final maturity 6 months or less)
1.00% (residual term to final maturity greater than 6 and up to and including 24 months)
1.60% (residual term to final maturity exceeding 24 months)Other BB+ to BB- 8.00% Below BB- 12.00% Unrated 8.00%
14.7
The government category will include all forms of government54 paper including bonds, treasury bills and other short-term instruments, but SAMA will reserve the right to apply a specific risk capital requirement to securities issued by certain foreign governments, especially to securities denominated in a currency other than that of the issuing government.
14.8 When the government paper is denominated in the domestic currency and funded by the bank in the same currency, at SAMA later stage discretion a lower specific risk capital requirement may be applied.
14.9 The qualifying category includes securities issued by public sector entities and multilateral development banks, plus other securities that are:
(1) rated investment grade (IG)55 by at least two credit rating agencies specified by SAMA; or
(2) rated IG by one rating agency and not less than IG by any other rating agency specified by SAMA (subject to SAMA and Capital Market Authority “CMA”); or
(3) subject to SAMA approval, unrated, but deemed to be of comparable investment quality by the reporting bank, and the issuer has securities listed on a recognised stock exchange.
14.10 SAMA will be responsible for monitoring the application of these qualifying criteria, particularly in relation to the last criterion where the initial classification is essentially left to the reporting banks. SAMA will also have discretion to include within the qualifying category debt securities issued by banks in countries which have implemented this framework, subject to the express understanding that SAMA undertake prompt remedial action if a bank fails to meet the capital standards set forth in this framework. Similarly, SAMA will have discretion to include within the qualifying category debt securities issued by securities firms that are subject to equivalent rules.
14.11 Furthermore, the qualifying category shall include securities issued by institutions that are deemed to be equivalent to IG quality and subject to SAMA regulatory arrangements comparable to those under this framework.
14.12 Unrated securities may be included in the qualifying category when they are subject to SAMA approval, unrated, but deemed to be of comparable investment quality by the reporting bank, and the issuer has securities listed on a recognised stock exchange. This will remain unchanged for banks using the simplified standardised approach. For banks using the internal ratings-based (IRB) approach for a portfolio, unrated securities can be included in the qualifying category if both of the following conditions are met:
(1) the securities are rated equivalent56 to IG under the reporting bank’s internal rating system, which SAMA has confirmed complies with the requirements for an IRB approach; and
(2) the issuer has securities listed on a recognised stock exchange.
14.13 However, since this may in certain cases considerably underestimate the specific risk for debt instruments which have a high yield to redemption relative to government debt securities, SAMA will have the discretion:
(1) to apply a higher specific risk charge to such instruments; and/or
(2) to disallow offsetting for the purposes of defining the extent of general market risk between such instruments and any other debt instruments.
14.14 The specific risk capital requirement of securitisation positions as defined in a 18.1 to 18.6 of SAMA Minimum Capital Requirements for Credit Risk that are held in the trading book is to be calculated according to the revised method for such positions in the banking book as set out in revisions to the securitisation framework. A bank shall calculate the specific risk capital requirement applicable to each net securitisation position by dividing the risk weight calculated as if it were held in the banking book by [12.5].
14.15 Banks may limit the capital requirement for an individual position in a credit derivative or securitisation instrument to the maximum possible loss. For a short risk position this limit could be calculated as a change in value due to the underlying names immediately becoming default risk-free. For a long risk position, the maximum possible loss could be calculated as the change in value in the event that all the underlying names were to default with zero recoveries. The maximum possible loss must be calculated for each individual position.
When a bank buys credit protection for an asset-backed security (ABS) tranche and (due to netting rules) the bank is treated as having a net short position, the simplified standardised capital requirement for the net short position is often determined by the max potential loss. This is particularly true when the underlying ABS tranche has been severely downgraded and written down. In particular, banks note that if the underlying ABS continues to deteriorate, the overall capital requirement progressively increases and is dominated by the charge against the short side of the hedged position.
Some examples (without and with off-set) illustrate how the Max Loss principle should apply.
Max loss without offset:
Suppose the bank has net long and net short positions that reference similar, but not the same, underlying assets. In other words the bank hedges an A-rated mezzanine residential mortgage-backed security (RMBS) tranche (notional = USD 100) with a credit default swap (CDS) on a similar but different A-rated mezzanine RMBS (also having notional = USD 100).
Suppose the RMBS tranche owned by the bank is now rated C, and has value of USD 15. Also assume that the value of the CDS on the different RMBS has a current value of USD 80. Further, suppose that the current value of the RMBS underlying this CDS is USD 20 and is also rated C. Finally, suppose that the CDS would be valued at USD –2 if the underlying RMBS tranche were to recover unexpectedly and become risk-free.
The correct treatment is as follows: min (USD 15, USD 15) (long leg) + min (USD 20, USD 82) (short leg) = USD 35.
No off-set would be permissible in this example, because the same underlying asset has not been hedged. The capital requirement should, therefore, be calculated by summing the charges against the long and short legs. The maximum loss principle would apply to each individual position.
Please note that the market value of the underlying has been applied in determining the exposure value of the CDS.
Max loss with offset:
Suppose the bank hedges an A-rated mezzanine RMBS tranche with a CDS referencing the same RMBS having notional of USD 100. Suppose the RMBS tranche is now rated C, and has value USD 15, while the current value of the CDS is USD 85. Suppose that the value of the CDS would equal USD –2 if the RMBS tranche were to recover unexpectedly and become risk-free.
In this example, if the CDS exactly matched the RMBS in tenor, then offsetting could potentially apply. In that instance, the capital requirement should equal 20% of max{min(USD 15, USD 15), min(USD 15, USD 87)} = USD 3.
If the tenors were not matched (ie maturity mismatch), then the capital requirement should equal max{min(USD 15, USD 15), min(USD 15, USD 87)} = USD 15.
Please note that the maximum loss principle cannot be applied on a portfolio basis.
14.16 Full allowance will be recognised for positions hedged by credit derivatives when the values of two legs (ie long and short) always move in the opposite direction and broadly to the same extent. This would be the case in the following situations, in which cases no specific risk capital requirement applies to both sides of the position:
(1) the two legs consist of completely identical instruments; or
(2) a long cash position (or credit derivative) is hedged by a total rate of return swap (or vice versa) and there is an exact match between the reference obligation and the underlying exposure (ie the cash position).57
According to [14.16] to [14.18], the offsetting treatment is applied to a cash position that is hedged by a credit derivative or a credit derivative that is hedged by another credit derivative, assuming there is an exact match in terms of the reference obligations. The illustration of the treatment would be as following:
[14.16] to [14.18], are applicable not only when the underlying position being hedged is a cash position, but also when the position being hedged is a credit default swap (CDS) or other credit derivative. They also apply regardless of whether the cash positions or reference obligations of the credit derivative are single-name or securitisation exposures.
For example, when a long cash position is hedged using a CDS, the 80% offset treatment of [14.17] (the partial allowance treatment of [14.18]) generally applies when the reference obligation of the CDS is the cash instrument being hedged and the currencies and remaining maturities of the two positions are (are not) identical. Similarly, when a purchased CDS is hedged with a sold CDS, the 80% offset treatment (the partial allowance treatment) generally applies when both the long and short CDSs have the same reference obligations and the currencies and remaining maturities of the long and short CDSs are (are not) identical. The full allowance (100% offset) treatment generally applies only when there is zero basis risk between the instrument being hedged and the hedging instrument, such as when a cash position is hedged with a total rate of return swap referencing the same cash instrument and there is no currency mismatch, or when a purchased CDS position is hedged by selling a CDS with identical terms in all respects, including reference obligation, currency, maturity, documentation clauses (eg credit payout events, methods for determining payouts for credit events, etc), and structure of fixed and variable payments over time.
It is worth noting that the conditions under which partial or full offsetting of risk positions that are subject to interest rate specific risk are narrowly defined. In practice, offsets between securitisation positions and credit derivatives are unlikely to be recognised in most cases due to the explicit requirements in [14.16] to [14.18] on reference names etc.
14.17 An 80% offset will be recognised when the value of two legs (ie long and short) always moves in the opposite direction but not broadly to the same extent. This would be the case when a long cash position (or credit derivative) is hedged by a credit default swap (CDS) or a credit-linked note (or vice versa) and there is an exact match in terms of the reference obligation, the maturity of both the reference obligation and the credit derivative, and the currency of the underlying exposure. In addition, key features of the credit derivative contract (eg credit event definitions, settlement mechanisms) should not cause the price movement of the credit derivative to materially deviate from the price movements of the cash position. To the extent that the transaction transfers risk (ie taking account of restrictive payout provisions such as fixed payouts and materiality thresholds), an 80% specific risk offset will be applied to the side of the transaction with the higher capital requirement, while the specific risk requirement on the other side will be zero.
14.18 Partial allowance will be recognised when the value of the two legs (ie long and short) usually moves in the opposite direction. This would be the case in the following situations:
(1) The position is captured in [14.16](2), but there is an asset mismatch between the reference obligation and the underlying exposure. Nonetheless, the position meets the requirements in [CRE22.86].
(2) The position is captured in [14.16](1) or [14.17] but there is a currency or maturity mismatch58 between the credit protection and the underlying asset.
(3) The position is captured in [14.17] but there is an asset mismatch between the cash position (or credit derivative) and the credit derivative hedge. However, the underlying asset is included in the (deliverable) obligations in the credit derivative documentation.
14.19 In each of these cases in [14.16] to [14.18], the following rule applies. Rather than adding the specific risk capital requirements for each side of the transaction (ie the credit protection and the underlying asset) only the higher of the two capital requirements will apply.
14.20 In cases not captured in [14.16] to [14.18], a specific risk capital requirement will be assessed against both sides of the position.
14.21 An nth-to-default credit derivative is a contract where the payoff is based on the nth asset to default in a basket of underlying reference instruments. Once the nth default occurs the transaction terminates and is settled.
(1) The capital requirement for specific risk for a first-to-default credit derivative is the lesser of:
(a) the sum of the specific risk capital requirements for the individual reference credit instruments in the basket; and
(b) the maximum possible credit event payment under the contract.
(2) Where a bank has a risk position in one of the reference credit instruments underlying a first-to-default credit derivative and this credit derivative hedges the bank’s risk position, the bank is allowed to reduce, with respect to the hedged amount, both the capital requirement for specific risk for the reference credit instrument and that part of the capital requirement for specific risk for the credit derivative that relates to this particular reference credit instrument. Where a bank has multiple risk positions in reference credit instruments underlying a first-to-default credit derivative, this offset is allowed only for that underlying reference credit instrument having the lowest specific risk capital requirement.
(3) The capital requirement for specific risk for an nth-to-default credit derivative with n greater than one is the lesser of:
(a) the sum of the specific risk capital requirements for the individual reference credit instruments in the basket but disregarding the (n-1) obligations with the lowest specific risk capital requirements; and
(b) the maximum possible credit event payment under the contract. For nth-to- default credit derivatives with n greater than 1, no offset of the capital requirement for specific risk with any underlying reference credit instrument is allowed.
(4) If a first or other nth-to-default credit derivative is externally rated, then the protection seller must calculate the specific risk capital requirement using the rating of the derivative and apply the respective securitisation risk weights as specified in [14.14], as applicable.
(5) The capital requirement against each net nth-to-default credit derivative position applies irrespective of whether the bank has a long or short position, ie obtains or provides protection.
The framework mentions only tranches and nth-to-default products explicitly, but not nth to n+m-th-to-default products (eg the value depends on the default of the 5th, 6th, 7th and 8th default in a pool; only in specific cases such as the same nominal for all underlyings can this product be represented by, for example, a 5% to 8% tranche). The nth to n+m-th-to- default products are covered in the framework, such products are to be decomposed into individual nth-to-default products and the rules for nth-to-default products in [14.21] apply.
In the example cited above, the capital requirement for a basket default swap covering defaults five to eight would be calculated as the sum of the capital requirements for a 5th- to-default swap, a 6th-to-default swap, a 7th-to-default swap and an 8th-to-default swap.
14.22 A bank must determine the specific risk capital requirement for the correlation trading portfolio (CTP) as follows:
(1) The bank computes:
(a) the total specific risk capital requirements that would apply just to the net long positions from the net long correlation trading exposures combined; and
(b) the total specific risk capital requirements that would apply just to the net short positions from the net short correlation trading exposures combined.
(2) The larger of these total amounts is then the specific risk capital requirement for the CTP.
The approach of taking the larger of the specific risk capital requirements for net long positions and the specific risk capital requirement for net short positions are not applied to leveraged securitisation positions or option products on securitisation positions. Leveraged securitisation positions and option products on securitisation positions are securitisation positions. They are not admissible for the CTP. The capital requirements for specific risk will be determined as the sum of the capital requirements for specific risk against net long and net short positions.
General market risk
14.23 The capital requirements for general market risk are designed to capture the risk of loss arising from changes in market interest rates. A choice between two principal methods of measuring the risk is permitted – a maturity method and a duration method. In each method, the capital requirement is the sum of four components:
(1) the net short or long position in the whole trading book;
(2) a small proportion of the matched positions in each time band (the “vertical disallowance”);
(3) a larger proportion of the matched positions across different time bands (the “horizontal disallowance”); and
(4) a net charge for positions in options, where appropriate (see [14.84] and [14.85]).
14.24 Separate maturity ladders should be used for each currency and capital requirements should be calculated for each currency separately and then summed with no offsetting between positions of the opposite sign. In the case of those currencies in which business is insignificant, separate maturity ladders for each currency are not required. Rather, the bank may construct a single maturity ladder and slot, within each appropriate time band, the net long or short position for each currency. However, these individual net positions are to be summed within each time band, irrespective of whether they are long or short positions, to produce a gross position figure.
14.25 In the maturity method (see [14.29] for the duration method), long or short positions in debt securities and other sources of interest rate exposures including derivative instruments, are slotted into a maturity ladder comprising 13 time bands (or 15 time bands in the case of low coupon instruments). Fixed rate instruments should be allocated according to the residual term to maturity and floating-rate instruments according to the residual term to the next repricing date. Opposite positions of the same amount in the same issues (but not different issues by the same issuer), whether actual or notional, can be omitted from the interest rate maturity framework, as well as closely matched swaps, forwards, futures and forward rate agreements (FRAs) which meet the conditions set out in [14.35] and [14.36] below.
14.26 The first step in the calculation is to weight the positions in each time band by a factor designed to reflect the price sensitivity of those positions to assumed changes in interest rates. The weights for each time band are set out in Table 4. Zero-coupon bonds and deep-discount bonds (defined as bonds with a coupon of less than 3%) should be slotted according to the time bands set out in the second column of Table 4.
Maturity method: time bands and weights Table 4 Coupon 3% or more Coupon less than 3% Risk weight Assumed changes in yield 1 month or less 1 month or less 0.00% 1.00 1 to 3 months 1 to 3 months 0.20% 1.00 3 to 6 months 3 to 6 months 0.40% 1.00 6 to 12 months 6 to 12 months 0.70% 1.00 1 to 2 years 1.0 to 1.9 years 1.25% 0.90 2 to 3 years 1.9 to 2.8 years 1.75% 0.80 3 to 4 years 2.8 to 3.6 years 2.25% 0.75 4 to 5 years 3.6 to 4.3 years 2.75% 0.75 5 to 7 years 4.3 to 5.7 years 3.25% 0.70 7 to 10 years 5.7 to 7.3 years 3.75% 0.65 10 to 15 years 7.3 to 9.3 years 4.50% 0.60 15 to 20 years 9.3 to 10.6 years 5.25% 0.60 Over 20 years 10.6 to 12 years 6.00% 0.60 12 to 20 years 8.00% 0.60 Over 20 years 12.50% 0.60
14.27
The next step in the calculation is to offset the weighted longs and shorts in each time band, resulting in a single short or long position for each band. Since, however, each band would include different instruments and different maturities, a 10% capital requirement to reflect basis risk and gap risk will be levied on the smaller of the offsetting positions, be it long or short. Thus, if the sum of the weighted longs in a time band is USD 100 million and the sum of the weighted shorts USD 90 million, the so-called vertical disallowance for that time band would be 10% of USD 90 million (ie USD 9 million).
14.28 The result of the above calculations is to produce two sets of weighted positions, the net long or short positions in each time band (USD 10 million long in the example above) and the vertical disallowances, which have no sign.
(1) In addition, however, banks will be allowed to conduct two rounds of horizontal offsetting:
(a) first between the net positions in each of three zones, where zone 1 is set as zero to one year, zone 2 is set as one year to four years, and zone 3 is set as four years and over (however, for coupons less than 3%, zone 2 is set as one year to 3.6 years and zone 3 is set as 3.6 years and over); and
(b) subsequently between the net positions in the three different zones.
(2) The offsetting will be subject to a scale of disallowances expressed as a fraction of the matched positions, as set out in Table 5. The weighted long and short positions in each of three zones may be offset, subject to the matched portion attracting a disallowance factor that is part of the capital requirement. The residual net position in each zone may be carried over and offset against opposite positions in other zones, subject to a second set of disallowance factors.
Horizontal disallowances Table 5 Zones59 Time band57 Within the zone Between adjacent zones Between zones 1 and 3 Zone 1 0-1 month
1-3 months
3-6 months
6-12 months
40% 40% 100% Zone 2 1-2 years
2-3 years
3-4 years
4-5 years
30% 40% Zone 3 5-7 years
7-10 years
10-15 years
15-20 years
Over 20 years30%
14.29
Under the alternative duration method, banks with the necessary capability may, with SAMA’ consent, use a more accurate method of measuring all of their general market risk by calculating the price sensitivity of each position separately. Banks must elect and use the method on a continuous basis (unless a change in method is approved by SAMA) and will be subject to SAMA monitoring of the systems used. The mechanics of this method are as follows:
(1) First calculate the price sensitivity of each instrument in terms of a change in interest rates of between 0.6 and 1.0 percentage points depending on the maturity of the instrument (see Table 6);
(2) Slot the resulting sensitivity measures into a duration-based ladder with the 15 time bands set out in Table 6;
(3) Subject long and short positions in each time band to a 5% vertical disallowance designed to capture basis risk; and
(4) Carry forward the net positions in each time band for horizontal offsetting subject to the disallowances set out in Table 5 above.
Duration method: time bands and assumed changes in yield Table 6 Assumed change in yield Assumed change in yield Zone 1: Zone 3: 1 month or less 1.00 3.6 to 4.3 years 0.75 1 to 3 months 1.00 4.3 to 5.7 years 0.70 3 to 6 months 1.00 5.7 to 7.3 years 0.65 6 to 12 months 1.00 7.3 to 9.3 years 0.60 Zone 2: 9.3 to 10.6 years 0.60 1.0 to 1.9 years 0.90 10.6 to 12 years 0.60 1.9 to 2.8 years 0.80 12 to 20 years 0.60 2.8 to 3.6 years 0.75 Over 20 years 0.60
14.30
In the case of residual currencies (see [14.24] above) the gross positions in each time band will be subject to either the risk weightings set out in [14.26], if positions are reported using the maturity method, or the assumed change in yield set out in [14.29], if positions are reported using the duration method, with no further offsets.
Interest rate derivatives
14.31 The measurement system should include all interest-rate derivatives and off- balance sheet instruments in the trading book which react to changes in interest rates (eg FRAs, other forward contracts, bond futures, interest rate and cross-currency swaps and forward foreign exchange positions). Options can be treated in a variety of ways as described in [14.74] to [14.86]. A summary of the rules for dealing with interest rate derivatives is set out in [14.40].
14.32 The derivatives should be converted into positions in the relevant underlying and become subject to specific and general market risk charges as described above. In order to calculate the standard formula described above, the amounts reported should be the market value of the principal amount of the underlying or of the notional underlying resulting from the Prudent Valuation Guidance.
14.33 Futures and forward contracts (including FRAs) are treated as a combination of a long and a short position in a notional government security. The maturity of a future or an FRA will be the period until delivery or exercise of the contract, plus – where applicable – the life of the underlying instrument. For example, a long position in a June three-month interest rate future (taken in April) is to be reported as a long position in a government security with a five-month maturity and a short position in a government security with a two-month maturity. Where a range of deliverable instruments may be delivered to fulfil the contract, the bank has flexibility to elect which deliverable security goes into the maturity or duration ladder but should take account of any conversion factor defined by the exchange. In the case of a future on a corporate bond index, positions will be included at the market value of the notional underlying portfolio of securities.
14.34 Swaps will be treated as two notional positions in government securities with relevant maturities. For example, an interest rate swap under which a bank is receiving floating rate interest and paying fixed will be treated as a long position in a floating rate instrument of maturity equivalent to the period until the next interest fixing and a short position in a fixed-rate instrument of
14.35 Banks may exclude from the interest rate maturity framework altogether (for both specific and general market risk) long and short positions (both actual and notional) in identical instruments with exactly the same issuer, coupon, currency and maturity. A matched position in a future or forward and its corresponding underlying may also be fully offset60 and thus excluded from the calculation. When the future or the forward comprises a range of deliverable instruments offsetting of positions in the future or forward contract and its underlying is only permissible in cases where there is a readily identifiable underlying security that is most profitable for the trader with a short position to deliver. The price of this security, sometimes called the “cheapest-to- deliver”, and the price of the future or forward contract should, in such cases, move in close alignment. No offsetting will be allowed between positions in different currencies; the separate legs of cross-currency swaps or forward FX deals are to be treated as notional positions in the relevant instruments and included in the appropriate calculation for each currency.
14.36 In addition, opposite positions in the same category of instruments61 can in certain circumstances be regarded as matched and allowed to offset fully. To qualify for this treatment, the positions must relate to the same underlying instruments, be of the same nominal value and be denominated in the same currency.62 In addition:
(1) for futures: offsetting positions in the notional or underlying instruments to which the futures contract relates must be for identical products and mature within seven days of each other;
(2) for swaps and FRAs: the reference rate (for floating rate positions) must be identical and the coupon closely matched (ie within 15 basis points); and
(3) for swaps, FRAs and forwards: the next interest fixing date or, for fixed coupon positions or forwards, the residual maturity must correspond within the following limits:
(a) less than one month hence: same day;
(b) between one month and one year hence: within seven days; and
(c) over one year hence: within 30 days.
14.37 Banks with large swap books may use alternative formulae for these swaps to calculate the positions to be included in the maturity or duration ladder. One method would be to first convert the payments required by the swap into their present values. For that purpose, each payment should be discounted using zero coupon yields, and a single net figure for the present value of the cash flows entered into the appropriate time band using procedures that apply to zero- (or low-) coupon bonds; these figures should be slotted into the general market risk framework as set out above. An alternative method would be to calculate the sensitivity of the net present value implied by the change in yield used in the maturity or duration method and allocate these sensitivities into the time bands set out in [14.26] or [14.29]. Other methods which produce similar results could also be used. Such alternative treatments will, however, only be allowed if:
(1) SAMA is fully satisfied with the accuracy of the systems being used;
(2) the positions calculated fully reflect the sensitivity of the cash flows to interest rate changes and are entered into the appropriate time bands; and
(3) the positions are denominated in the same currency.
14.38 Interest rate and currency swaps, FRAs, forward FX contracts and interest rate futures will not be subject to a specific risk charge. This exemption also applies to futures on an interest rate index (eg London Interbank Offer Rate, or LIBOR). However, in the case of futures contracts where the underlying is a debt security, or an index representing a basket of debt securities, a specific risk charge will apply according to the credit risk of the issuer as set out in [14.5] to [14.21].
14.39 General market risk applies to positions in all derivative products in the same manner as for cash positions, subject only to an exemption for fully or very closely matched positions in identical instruments as defined in [paragraphs 718(xiii) and 718(xiv) / [14.35] and [14.36]. The various categories of instruments should be slotted into the maturity ladder and treated according to the rules identified earlier.
14.40 Table 7 presents a summary of the regulatory treatment for interest rate derivatives, for market risk purposes.
Summary of treatment of interest rate derivatives Table 7 Instrument Specific risk charge63 General market risk charge Exchanged-traded future Government debt security Yes64 Yes, as two positions Corporate debt security Yes Yes, as two positions Index on interest rates (eg LIBOR) No Yes, as two positions Over-the-counter (OTC) forward Government debt security Yes63 Yes, as two positions Corporate debt security Yes Yes, as two positions Index on interest rates No Yes, as two positions FRAs, swaps No Yes, as two positions Forward FX
No Yes, as one position in each currency
Options
Either
Government debt security Yes63 (a) carve out together with the associated hedging positions: simplified approach; scenario analysis; internal models
Corporate debt security Yes (b) general market risk charge according to the delta-plus method (gamma and vega should receive separate capital requirements) Index on interest rates No FRAs, swaps No 53 Traded mortgage securities and mortgage derivative products possess unique characteristics because of the risk of prepayment. Accordingly, for the time being, no common treatment will apply to these securities, which will be dealt with SAMA at aleates stage. A security that is the subject of a repurchase or securities lending agreement will be treated as if it were still owned by the lender of the security, ie it will be treated in the same manner as other securities positions.
54 Including, local and regional governments subject to a zero credit risk weight in the credit risk framework.
55 For example, IG include rated Baa or higher by Moody’s and BBB or higher by Standard and Poor’s.
56 Equivalent means the debt security has a one-year probability of default (PD) equal to or less than the one year PD implied by the long-run average one-year PD of a security rated IG or better by a qualifying rating agency.
57 The maturity of the swap itself may be different from that of the underlying exposure.
58 Currency mismatches should feed into the normal reporting of FX risk.
59 The zones for coupons less than 3% are 0 to 1 year, 1 to 3.6 years, and 3.6 years and over.
60 The leg representing the time to expiry of the future should, however, be reported.
61 This includes the delta-equivalent value of options. The delta equivalent of the legs arising out of the treatment of caps and floors as set out in [14.78] can also be offset against each other under the rules laid down in this paragraph.
62 The separate legs of different swaps may also be matched subject to the same conditions.
63 This is the specific risk charge relating to the issuer of the instrument. Under the credit risk rules, a separate capital requirement for the counterparty credit risk applies.
64 The specific risk capital requirement only applies to government debt securities that are rated below AA– (see [14.6] and [14.7]).Equity Risk
14.41 This section sets out a minimum capital standard to cover the risk of holding or taking positions in equities in the trading book. It applies to long and short positions in all instruments that exhibit market behaviour similar to equities, but not to non-convertible preference shares (which are covered by the interest rate risk requirements described in [14.3] to [14.40]). Long and short positions in the same issue may be reported on a net basis. The instruments covered include common stocks (whether voting or non-voting), convertible securities that behave like equities, and commitments to buy or sell equity securities. The treatment of derivative products, stock indices and index arbitrage is described in [14.44] to [14.52] below.
Specific and general market risks
14.42 As with debt securities, the minimum capital standard for equities is expressed in terms of two separately calculated capital requirements for the specific risk of holding a long or short position in an individual equity and for the general market risk of holding a long or short position in the market as a whole. Specific risk is defined as the bank’s gross equity positions (ie the sum of all long equity positions and of all short equity positions) and general market risk as the difference between the sum of the longs and the sum of the shorts (ie the overall net position in an equity market).The long or short position in the market must be calculated on a market-by-market basis, ie a separate calculation has to be carried out for each national market in which the bank holds equities.
14.43 The capital requirement for specific risk and for general market risk will each be 8%.
Equity derivatives
14.44 Except for options, which are dealt with in [14.74] to [14.86], equity derivatives and off- balance sheet positions that are affected by changes in equity prices should be included in the measurement system.65 This includes futures and swaps on both individual equities and on stock indices. The derivatives are to be converted into positions in the relevant underlying. The treatment of equity derivatives is summarised in [14.52] below.
14.45 In order to calculate the standard formula for specific and general market risk, positions in derivatives should be converted into notional equity positions:
(1) Futures and forward contracts relating to individual equities should in principle be reported at current market prices.
(2) Futures relating to stock indices should be reported as the marked-to-market value of the notional underlying equity portfolio.
(3) Equity swaps are to be treated as two notional positions.66
(4) Equity options and stock index options should be either carved out together with the associated underlyings or be incorporated in the measure of general market risk described in this section according to the delta-plus method.
14.46 Matched positions in each identical equity or stock index in each market may be fully offset, resulting in a single net short or long position to which the specific and general market risk charges will apply. For example, a future in a given equity may be offset against an opposite cash position in the same equity.67
14.47 Besides general market risk, a further capital requirement of 2% will apply to the net long or short position in an index contract comprising a diversified portfolio of equities. This capital requirement is intended to cover factors such as execution risk. SAMA will take care to ensure that this 2% risk weight applies only to well- diversified indices and not, for example, to sectoral indices.
14.48 In the case of the futures-related arbitrage strategies described below, the additional 2% capital requirement described above (set out in [14.47]) may be applied to only one index with the opposite position exempt from a capital requirement. The strategies are:
(1) when the bank takes an opposite position in exactly the same index at different dates or in different market centres; and
(2) When the bank has an opposite position in contracts at the same date in different but similar indices, subject to SAMA oversight that the two indices contain sufficient common components to justify offsetting.
14.49 Where a bank engages in a deliberate arbitrage strategy, in which a futures contract on a broadly based index matches a basket of stocks, it will be allowed to carve out both positions from the simplified standardised approach on condition that:
(1) the trade has been deliberately entered into and separately controlled; and
(2) the composition of the basket of stocks represents at least 90% of the index when broken down into its notional components.
14.50 In such a case as set out in [14.49] the minimum capital requirement will be 4% (ie 2% of the gross value of the positions on each side) to reflect divergence and execution risks. This applies even if all of the stocks comprising the index are held in identical proportions. Any excess value of the stocks comprising the basket over the value of the futures contract or excess value of the futures contract over the value of the basket is to be treated as an open long or short position.
14.51 If a bank takes a position in depository receipts against an opposite position in the underlying equity or identical equities in different markets, it may offset the position (ie bear no capital requirement) but only on condition that any costs on conversion are fully taken into account.68
14.52 Table 8 summarises the regulatory treatment of equity derivatives for market risk purposes.
Summary of treatment of equity derivatives
Table 8
Instrument
Specific risk69
General market risk
Exchanged-traded or OTC future
Individual equity
Yes
Yes, as underlying
Index
2%
Yes, as underlying
Options
Either
Individual equity
Yes
(a) carve out together with the associated hedging positions: simplified approach; scenario analysis; internal models
Index 2% (b) general market risk charge according to the delta-plus method (gamma and vega should receive separate capital requirements) 65 Where equities are part of a forward contract, a future or an option (quantity of equities to be received or to be delivered), any interest rate or foreign currency exposure from the other leg of the contract should be reported as set out in [14.3] to [14.40] and [14.53] to [14.62].
66 For example, an equity swap in which a bank is receiving an amount based on the change in value of one particular equity or stock index and paying a different index will be treated as a long position in the former and a short position in the latter. Where one of the legs involves receiving/paying a fixed or floating interest rate, that exposure should be slotted into the appropriate repricing time band for interest rate related instruments as set out in [14.3] to [14.40]. The stock index should be covered by the equity treatment.
67 The interest rate risk arising out of the future, however, should be reported as set out in [14.3] to [14.40].
68 Any FX risk arising out of these positions has to be reported as set out in [14.53] to [14.67].
69 This is the specific risk charge relating to the issuer of the instrument. Under the credit risk rules], a separate capital requirement for the counterparty credit risk applies.Foreign Exchange Risk
14.53 This section sets out the simplified standardised approach for measuring the risk of holding or taking positions in foreign currencies, including gold.70
14.54 Two processes are needed to calculate the capital requirement for FX risk.
(1) The first is to measure the exposure in a single currency position as set out in [14.55] to [14.58].
(2) The second is to measure the risks inherent in a bank’s mix of long and short positions in different currencies as set out in [14.59] to [14.62].
Measuring the exposure in a single currency
14.55 The bank’s net open position in each currency should be calculated by summing:
(1) the net spot position (ie all asset items less all liability items, including accrued interest, denominated in the currency in question);
(2) the net forward position (ie all amounts to be received less all amounts to be paid under forward FX transactions, including currency futures and the principal on currency swaps not included in the spot position);
(3) guarantees (and similar instruments) that are certain to be called and are likely to be irrecoverable;
(4) net future income/expenses not yet accrued but already fully hedged (at the discretion of the reporting bank);
(5) any other item representing a profit or loss in foreign currencies (depending on particular accounting conventions in different countries); and
(6) the net delta-based equivalent of the total book of foreign currency options.71
14.56 Positions in composite currencies need to be separately reported but, for measuring banks’ open positions, may be either treated as a currency in their own right or split into their component parts on a consistent basis. Positions in gold should be measured in the same manner as described in [14.68].72
14.57 Interest, other income and expenses should be treated as follows. Interest accrued (ie earned but not yet received) should be included as a position. Accrued expenses should also be included. Unearned but expected future interest and anticipated expenses may be excluded unless the amounts are certain and banks have taken the opportunity to hedge them. If banks include future income/expenses they should do so on a consistent basis, and not be permitted to select only those expected future flows which reduce their position.
14.58 Forward currency and gold positions should be measured as follows: Forward currency and gold positions will normally be valued at current spot market exchange rates. Using forward exchange rates would be inappropriate since it would result in the measured positions reflecting current interest rate differentials to some extent. However, banks that base their normal management accounting on net present values are expected to use the net present values of each position, discounted using current interest rates and valued at current spot rates, for measuring their forward currency and gold positions.
Measuring the foreign exchange risk in a portfolio of foreign currency positions and gold
14.59 For measuring the FX risk in a portfolio of foreign currency positions and gold as set out in [14.54](2), a bank that is not approved to use internal models by SAMA must use a shorthand method which treats all currencies equally.
14.60 Under the shorthand method, the nominal amount (or net present value) of the net position in each foreign currency and in gold is converted at spot rates into the reporting currency.73 The overall net open position is measured by aggregating:
(1) the sum of the net short positions or the sum of the net long positions, whichever is the greater;74 plus
(2) the net position (short or long) in gold, regardless of sign.
14.61 The capital requirement will be 8% of the overall net open position (see example in Table 9). In particular, the capital requirement would be 8% of the higher of either the net long currency positions or the net short currency positions (ie 300) and of the net position in gold (35) = 335 x 8% = 26.8.
Example of the shorthand measure of FX risk Table 9 JPY EUR GBP CAD USD Gold Net position per currency +50 + 100 + 150 -20 -180 -35 Net open position +300 -200 35
14.62
A bank of which business in foreign currency is insignificant and which does not take FX positions for its own account may, at the discretion of SAMA, be exempted from capital requirements on these positions provided that:
(1) its foreign currency business, defined as the greater of the sum of its gross long positions and the sum of its gross short positions in all foreign currencies, does not exceed 100% of eligible capital as defined in Regulatory Capital for Basel III in Finalized Guidance Document Concerning the Implementation of Basel III issued by SAMA in 19 December 2012 and any subsequent regulatory adjustments; and
(2) its overall net open position as defined in [14.60] above does not exceed 2% of its eligible capital as defined in Regulatory Capital for Basel III in Finalized Guidance Document Concerning the Implementation of Basel III issued by SAMA in 19 December 2012 and any subsequent regulatory adjustments .
70 Gold is to be dealt with as an FX position rather than a commodity because its volatility is more in line with foreign currencies and banks manage it in a similar manner to foreign currencies.
71 Subject to a separately calculated capital requirement for gamma and vega as described in [14.77] to [14.80]; alternatively, options and their associated underlyings are subject to one of the other methods described in [14.74] to [14.86].
72 Where gold is part of a forward contract (quantity of gold to be received or to be delivered), any interest rate or foreign currency exposure from the other leg of the contract should be reported as set out in [14.3] to [14.40] and 14.55] above.
73 Where the bank is assessing its FX risk on a consolidated basis, it may be technically impractical in the case of some marginal operations to include the currency positions of a foreign branch or subsidiary of the bank. In such cases, the internal limit in each currency may be used as a proxy for the positions. Provided there is adequate ex post monitoring of actual positions against such limits, the limits should be added, without regard to sign, to the net open position in each currency.
74 An alternative calculation, which produces an identical result, is to include the reporting currency as a residual and to take the sum of all the short (or long) positions.Commodities Risk
14.63 This section sets out the simplified standardised approach for measuring the risk of holding or taking positions in commodities, including precious metals, but excluding gold (which is treated as a foreign currency according to the methodology set out in [14.53] to [14.62] above). A commodity is defined as a physical product which is or can be traded on a secondary market, eg agricultural products, minerals (including oil) and precious metals.
14.64 The price risk in commodities is often more complex and volatile than that associated with currencies and interest rates. Commodity markets may also be less liquid than those for interest rates and currencies and, as a result, changes in supply and demand can have a more dramatic effect on price and volatility.75 These market characteristics can make price transparency and the effective hedging of commodities risk more difficult.
14.65 The risks associated with commodities include the following risks:
(1) For spot or physical trading, the directional risk arising from a change in the spot price is the most important risk.
(2) However, banks using portfolio strategies involving forward and derivative contracts are exposed to a variety of additional risks, which may well be larger than the risk of a change in spot prices. These include:
(a) basis risk (the risk that the relationship between the prices of similar commodities alters through time);
(b) interest rate risk (the risk of a change in the cost of carry for forward positions and options); and
(c) forward gap risk (the risk that the forward price may change for reasons other than a change in interest rates).
(3) In addition, banks may face counterparty credit risk on over-the-counter derivatives, but this is captured by one of the methods set out in 5 to 9 and 11 of SAMA Minimum Capital Requirements for Counterparty Credit Risk (CCR) and Credit Valuation Adjustment (CVA)
(4) The funding of commodities positions may well open a bank to interest rate or FX exposure and if that is so the relevant positions should be included in the measures of interest rate and FX risk described in [14.3] to [14.40] and [14.53] to [14.62], respectively.76
14.66 There are two alternatives for measuring commodities position risk under the simplified standardised approach that are described in [14.68] to [14.73] below. Commodities risk can also be measured, using either (i) the maturity ladder approach, which is a measurement system that captures forward gap and interest rate risk separately by basing the methodology on seven time bands as set out in [14.68] to [14.71] below or (ii) the simplified approach, which is a very simple framework as set out in [14.72] and [14.73] below. Both the maturity ladder approach and the simplified approach are appropriate only for banks that, in relative terms, conduct only a limited amount of commodities business.
14.67 For the maturity ladder approach and the simplified approach, long and short positions in each commodity may be reported on a net basis for the purposes of calculating open positions. However, positions in different commodities will, as a general rule, not be offsettable in this fashion. Nevertheless, SAMA will have discretion to permit netting between different subcategories77 of the same commodity in cases where the subcategories are deliverable against each other. They can also be considered as offsettable if they are close substitutes against each other and a minimum correlation of 0.9 between the price movements can be clearly established over a minimum period of one year. However, a bank wishing to base its calculation of capital requirements for commodities on correlations would have to satisfy SAMA of the accuracy of the method that has been chosen and obtain its prior approval.
Maturity ladder approach
14.68 In calculating the capital requirements under the maturity ladder approach, banks will first have to express each commodity position (spot plus forward) in terms of the standard unit of measurement (barrels, kilos, grams etc). The net position in each commodity will then be converted at current spot rates into the national currency.
14.69 Secondly, in order to capture forward gap and interest rate risk within a time band (which, together, are sometimes referred to as curvature/spread risk), matched long and short positions in each time band will carry a capital requirement. The methodology is similar to that used for interest rate related instruments as set out in [14.3] to [14.40]. Positions in the separate commodities (expressed in terms of the standard unit of measurement) will first be entered into a maturity ladder while physical stocks should be allocated to the first time band. A separate maturity ladder will be used for each commodity as defined in [14.67] above.78 For each time band as set out in Table 10, the sum of short and long positions that are matched will be multiplied first by the spot price for the commodity, and then by the spread rate of 1.5%.
Time bands and spread rates Table 10 Time band Spread rate 0-1 month 1.5% 1-3 months 1.5% 3-6 months 1.5% 6-12 months 1.5% 1-2 years 1.5% 2-3 years 1.5% over 3 years 1.5%
14.70
The residual net positions from nearer time bands may then be carried forward to offset exposures in time bands that are further out. However, recognising that such hedging of positions among different time bands is imprecise, a surcharge equal to 0.6% of the net position carried forward will be added in respect of each time band that the net position is carried forward. The capital requirement for each matched amount created by carrying net positions forward will be calculated as in [14.69] above. At the end of this process, a bank will have either only long or only short positions, to which a capital requirement of 15% will apply.
14.71 All commodity derivatives and off-balance sheet positions that are affected by changes in commodity prices should be included in this measurement framework. This includes commodity futures, commodity swaps, and options where the “delta-plus” method79 is used (see [14.77] to [14.80] below). In order to calculate the risk, commodity derivatives should be converted into notional commodities positions and assigned to maturities as follows:
(1) Futures and forward contracts relating to individual commodities should be incorporated as notional amounts of the standard unit of measurement (barrels, kilos, grams etc) and should be assigned a maturity with reference to expiry date.
(2) Commodity swaps where one leg is a fixed price and the other the current market price should be incorporated as a series of positions equal to the notional amount of the contract, with one position corresponding with each payment on the swap and slotted into the maturity ladder accordingly. The positions would be long positions if the bank is paying fixed and receiving floating, and short positions if the bank is receiving fixed and paying floating.80
(3) Commodity swaps where the legs are in different commodities are to be incorporated in the relevant maturity ladder. No offsetting will be allowed in this regard except where the commodities belong to the same subcategory as defined in [14.67] above.
Simplified approach
14.72 In calculating the capital requirement for directional risk under the simplified approach, the same procedure will be adopted as in the maturity ladder approach described above (see [14.68] and [14.71]. Once again, all commodity derivatives and off-balance sheet positions that are affected by changes in commodity prices should be included. The capital requirement will equal 15% of the net position, long or short, in each commodity.
14.73 In order to protect the bank against basis risk, interest rate risk and forward gap risk under the simplified approach, the capital requirement for each commodity as described in [14.68] and [14.71] above will be subject to an additional capital requirement equivalent to 3% of the bank’s gross positions, long plus short, in that particular commodity. In valuing the gross positions in commodity derivatives for this purpose, banks should use the current spot price.
75 Banks need also to guard against the risk that arises when the short position falls due before the long position. Owing to a shortage of liquidity in some markets, it might be difficult to close the short position and the bank might be squeezed by the market.
76 Where a commodity is part of a forward contract (quantity of commodities to be received or to be delivered), any interest rate or foreign currency exposure from the other leg of the contract should be reported as set out in [14.3] to 14.40] and [14.53] to [14.62]. Positions which are purely stock financing (ie a physical stock has been sold forward and the cost of funding has been locked in until the date of the forward sale) may be omitted from the commodities risk calculation although they will be subject to interest rate and counterparty risk requirements.
77 Commodities can be grouped into clans, families, subgroups and individual commodities. For example, a clan might be Energy Commodities, within which Hydro-Carbons are a family with Crude Oil being a subgroup and West Texas Intermediate, Arabian Light and Brent being individual commodities.
78 For markets that have daily delivery dates, any contracts maturing within 10 days of one another may be offset.
79 For banks using other approaches to measure options risk, all options and the associated underlyings should be excluded from both the maturity ladder approach and the simplified approach.
80 If one of the legs involves receiving/paying a fixed or floating interest rate, that exposure should be slotted into the appropriate repricing maturity band in the maturity ladder covering interest rate related instruments.Treatment of Options
14.74 In recognition of the wide diversity of banks’ activities in options and the difficulties of measuring price risk for options, two alternative approaches will be permissible at the discretion of SAMA under the simplified standardised approach.
(1) Those banks which solely use purchased options81 can use the simplified approach described in [14.76] below];
(2) Those banks which also write options are expected to use the delta-plus method or scenario approach which are the intermediate approaches as set out in [14.77] to [14.86]. The more significant its trading activity is, the more the bank will be expected to use a sophisticated approach, and a bank with highly significant trading activity is expected to use the standardised approach or the internal models approach as set out in [6] to [9] or [10] to [13].
14.75 In the simplified approach for options, the positions for the options and the associated underlying, cash or forward, are not subject to the standardised methodology but rather are carved-out and subject to separately calculated capital requirements that incorporate both general market risk and specific risk. The risk numbers thus generated are then added to the capital requirements for the relevant category, ie interest rate related instruments, equities, FX and commodities as described in [14.3] to [14.73]. The delta-plus method uses the sensitivity parameters or Greek letters associated with options to measure their market risk and capital requirements. Under this method, the delta-equivalent position of each option becomes part of the simplified standardised approach set out in [14.3] to [14.73] with the delta- equivalent amount subject to the applicable general market risk charges. Separate capital requirements are then applied to the gamma and vega risks of the option positions. The scenario approach uses simulation techniques to calculate changes in the value of an options portfolio for changes in the level and volatility of its associated underlyings. Under this approach, the general market risk charge is determined by the scenario grid (ie the specified combination of underlying and volatility changes) that produces the largest loss. For the delta-plus method and the scenario approach, the specific risk capital requirements are determined separately by multiplying the delta-equivalent of each option by the specific risk weights set out in [14.3] to [14.52].
Simplified approach
14.76 Banks that handle a limited range of purchased options can use the simplified approach set out in Table 11 for particular trades. As an example of how the calculation would work, if a holder of 100 shares currently valued at USD 10 each holds an equivalent put option with a strike price of USD 11, the capital requirement would be: USD 1,000 x 16% (ie 8% specific plus 8% general market risk) = USD 160, less the amount the option is in the money (USD 11 - USD 10) x 100 = USD 100, ie the capital requirement would be USD 60. A similar methodology applies for options whose underlying is a foreign currency, an interest rate related instrument or a commodity.
Simplified approach: capital requirements
Table 11
Position
Treatment
Long cash and long put or short cash and long call
The capital requirement will be the market value of the underlying security82 multiplied by the sum of specific and general market risk charges83 for the underlying less the amount the option is in the money (if any) bounded at zero84
Long call or long put The capital requirement will be the lesser of: (i) the market value of the underlying security multiplied by the sum of specific and general market risk charges82 for the underlying and (ii) the market value of the option85
Delta-plus method
14.77 Banks that write options will be allowed to include delta-weighted options positions within the simplified standardised approach set out in [14.3] to [14.73]. Such options should be reported as a position equal to the market value of the underlying multiplied by the delta. However, since delta does not sufficiently cover the risks associated with options positions, banks will also be required to measure gamma (which measures the rate of change of delta) and vega (which measures the sensitivity of the value of an option with respect to a change in volatility) sensitivities in order to calculate the total capital requirement. These sensitivities will be calculated according to an approved exchange model or to the bank’s proprietary options pricing model subject to oversight by SAMA.86
14.78 Delta-weighted positions with debt securities or interest rates as the underlying will be slotted into the interest rate time bands, as set out in [14.3] to [14.40], under the following procedure. A two-legged approach should be used as for other derivatives, requiring one entry at the time the underlying contract takes effect and a second at the time the underlying contract matures. For instance, a bought call option on a June three-month interest-rate future will in April be considered, on the basis of its delta-equivalent value, to be a long position with a five-month maturity and a short position with a two-month maturity.87 The written option will be similarly slotted as a long position with a two-month maturity and a short position with a five-month maturity. Floating rate instruments with caps or floors will be treated as a combination of floating rate securities and a series of European-style options. For example, the holder of a three-year floating rate bond indexed to six month LIBOR with a cap of 15% will treat it as:
(1) a debt security that reprices in six months; and
(2) a series of five written call options on an FRA with a reference rate of 15%, each with a negative sign at the time the underlying FRA takes effect and a positive sign at the time the underlying FRA matures.88
14.79 The capital requirement for options with equities as the underlying will also be based on the delta-weighted positions that will be incorporated in the measure of equity risk described in [14.41] to [14.52]. For purposes of this calculation each national market is to be treated as a separate underlying. The capital requirement for options on FX and gold positions will be based on the method for FX rate risk as set out in [14.53] to [14.62]. For delta risk, the net delta-based equivalent of the foreign currency and gold options will be incorporated into the measurement of the exposure for the respective currency (or gold) position. The capital requirement for options on commodities will be based on the simplified or the maturity ladder approach for commodities risk as set out in [14.63] to [14.73]. The delta-weighted positions will be incorporated in one of the measures described in that section.
14.80 In addition to the above capital requirements arising from delta risk, there are further capital requirements for gamma and vega risk. Banks using the delta-plus method will be required to calculate the gamma and vega for each option position (including hedge positions) separately. The capital requirements should be calculated in the following way:
(1) For each individual option a gamma impact should be calculated according to a Taylor series expansion as follows, where VU is the variation of the underlying of the option.
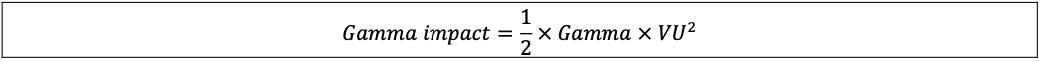
(2) VU is calculated as follows:
(a) For interest rate options if the underlying is a bond, the market value of the underlying should be multiplied by the risk weights set out in [14.26]. An equivalent calculation should be carried out where the underlying is an interest rate, again based on the assumed changes in the corresponding yield in [14.26].
(b) For options on equities and equity indices: the market value of the underlying should be multiplied by 8%.89
(c) For FX and gold options: the market value of the underlying should be multiplied by 8%.
(d) For options on commodities: the market value of the underlying should be multiplied by 15%.
(3) For the purpose of this calculation the following positions should be treated as the same underlying:
(a) for interest rates,90 each time band as set out in [paragraph 718(iv) / [14.26];91
(b) for equities and stock indices, each national market;
(c) for foreign currencies and gold, each currency pair and gold; and
(d) for commodities, each individual commodity as defined in [14.67].
(4) Each option on the same underlying will have a gamma impact that is either positive or negative. These individual gamma impacts will be summed, resulting in a net gamma impact for each underlying that is either positive or negative. Only those net gamma impacts that are negative will be included in the capital requirement calculation.
(5) The total gamma risk capital requirement will be the sum of the absolute value of the net negative gamma impacts as calculated above.
(6) For volatility risk, banks will be required to calculate the capital requirements by multiplying the sum of the vega risks for all options on the same underlying, as defined above, by a proportional shift in volatility of ± 25%.
(7) The total capital requirement for vega risk will be the sum of the absolute value of the individual capital requirements that have been calculated for vega risk.
Scenario approach
14.81 More sophisticated banks may opt to base the market risk capital requirement for options portfolios and associated hedging positions on scenario matrix analysis. This will be accomplished by specifying a fixed range of changes in the option portfolio’s risk factors and calculating changes in the value of the option portfolio at various points along this grid. For the purpose of calculating the capital requirement, the bank will revalue the option portfolio using matrices for simultaneous changes in the option’s underlying rate or price and in the volatility of that rate or price. A different matrix will be set up for each individual underlying as defined in [14.80] above. As an alternative, at the discretion of SAMA, banks that are significant traders in options will for interest rate options be permitted to base the calculation on a minimum of six sets of time bands. When using this method, not more than three of the time bands as defined in [14.26] and [14.29] should be combined into any one set.
14.82 The options and related hedging positions will be evaluated over a specified range above and below the current value of the underlying. The range for interest rates is consistent with the assumed changes in yield in [14.26]. Those banks using the alternative method for interest rate options set out in [14.81] above should use, for each set of time bands, the highest of the assumed changes in yield applicable to the group to which the time bands belong.92 The other ranges are ± 8% for equities,93 ± 8% for FX and gold, and ± 15% for commodities. For all risk categories, at least seven observations (including the current observation) should be used to divide the range into equally spaced intervals.
14.83 The second dimension of the matrix entails a change in the volatility of the underlying rate or price. A single change in the volatility of the underlying rate or price equal to a shift in volatility of + 25% and - 25% is expected to be sufficient in most cases. As circumstances warrant, however, SAMA may choose to require that a different change in volatility be used and/or that intermediate points on the grid be calculated.
14.84 After calculating the matrix, each cell contains the net profit or loss of the option and the underlying hedge instrument. The capital requirement for each underlying will then be calculated as the largest loss contained in the matrix.
14.85 The application of the scenario analysis by any specific bank will be subject to SAMA consent, particularly as regards the precise way that the analysis is constructed. Banks’ use of scenario analysis as part of the simplified standardised approach will also be subject to validation by SAMA, and to those of the qualitative standards for internal models as set out in [10].
14.86 Besides the options risks mentioned above, SAMA is conscious of the other risks also associated with options, eg rho (rate of change of the value of the option with respect to the interest rate) and theta (rate of change of the value of the option with respect to time). While not proposing a measurement system for those risks at present, it expects banks undertaking significant options business at the very least to monitor such risks closely. Additionally, banks will be permitted to incorporate rho into their capital calculations for interest rate risk, if they wish to do so.
81 Unless all their written option positions are hedged by perfectly matched long positions in exactly the same options, in which case no capital requirement for market risk is required.
82 In some cases such as FX, it may be unclear which side is the underlying security; this should be taken to be the asset that would be received if the option were exercised. In addition, the nominal value should be used for items where the market value of the underlying instrument could be zero, eg caps and floors, swaptions etc.
83 Some options (eg where the underlying is an interest rate, a currency or a commodity) bear no specific risk but specific risk will be present in the case of options on certain interest rate related instruments (eg options on a corporate debt security or corporate bond index; see [14.3] to [14.40] for the relevant capital requirements) and for options on equities and stock indices (see [14.41] to [14.52]). The charge under this measure for currency options will be 8% and for options on commodities 15%.
84 For options with a residual maturity of more than six months, the strike price should be compared with the forward, not current, price. A bank unable to do this must take the in the money amount to be zero.
85 Where the position does not fall within the trading book (ie options on certain FX or commodities positions not belonging to the trading book), it may be acceptable to use the book value instead.
86 SAMA may wish to require banks doing business in certain classes of exotic options (eg barriers, digitals) or in options at the money that are close to expiry to use either the scenario approach or the internal models alternative, both of which can accommodate more detailed revaluation approaches.
87 A two-month call option on a bond future where delivery of the bond takes place in September would be considered in April as being long the bond and short a five-month deposit, both positions being delta-weighted.
88 The rules applying to closely matched positions set out in [14.36] will also apply in this respect.
89 The basic rules set out here for interest rate and equity options do not attempt to capture specific risk when calculating gamma capital requirements. Hoever, SAMA may wish to require specific banks to do so.
90 Positions have to be slotted into separate maturity ladders by currency.
91 Banks using the duration method should use the time bands as set out in [14.29].
92 If, for example, the time bands 3 to 4 years, 4 to 5 years and 5 to 7 years are combined the highest assumed change in yield of these three bands would be 0.75.
93 The basic rules set out here for interest rate and equity options do not attempt to capture specific risk when calculating gamma capital requirements. However, SAMA may wish to require specific banks to do so.

